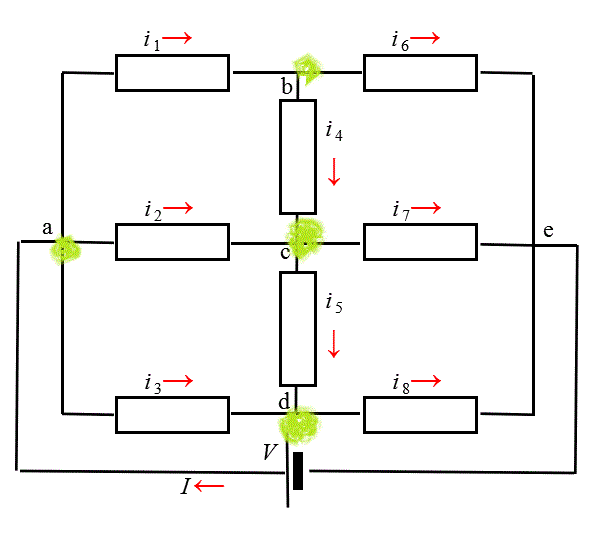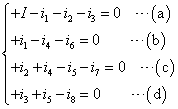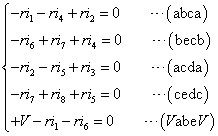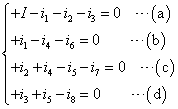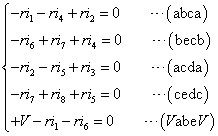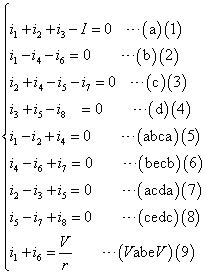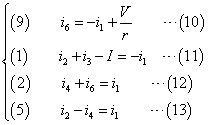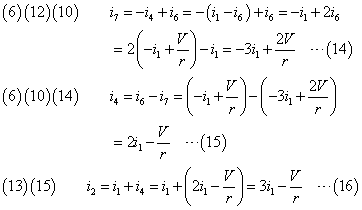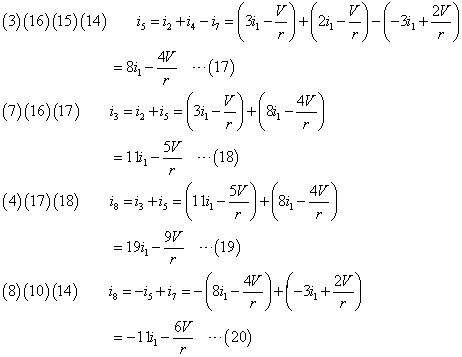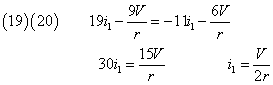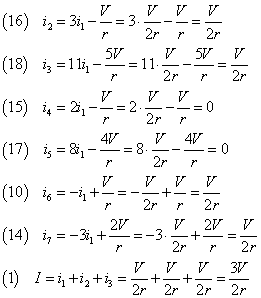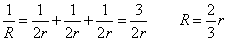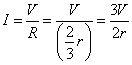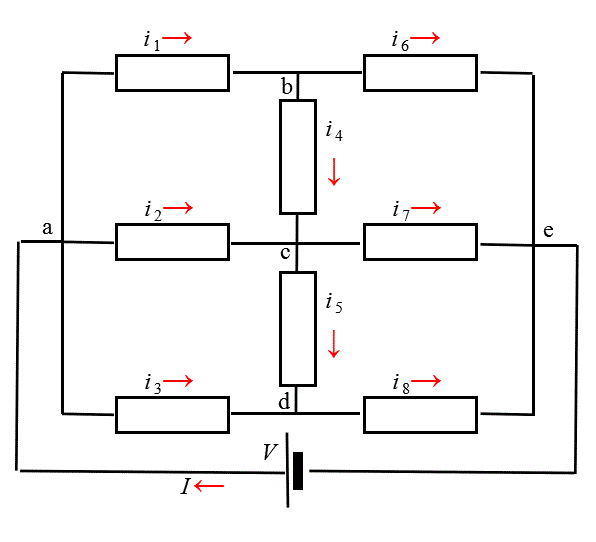
上図のような回路があって、抵抗は、いずれも同じ大きさ、rであるという。各抵抗を流れる電流を計算せよ、という訳だ。
抵抗は8個あって、これに加えて電源を流れる電流もあるから、合計9個の電流が「未知数」となる。上のように名づける。
未知数の個数に等しい条件式が存在して、はじめて、解を得る「可能性」があることを、線形代数学は教えてくれる。だから、9個の「条件式」を発見しなければならない。
条件式を導く「定理」は、以下の二つである。
- キルヒホッフ第1法則:「枝分かれ」の生じるポイントで、流入する電流をプラス、流出する電流をマイナスとして加算すると、合計が0になるはずだ。電流は{A=C/s}、単位時間あたりに通過する電荷量だから、これは、電荷に関する「保存則」となっている。
- キルヒホッフ第2法則:「閉回路」において、ある基準面からスタートして、回路に沿って電位差を加算していくと、基準面に戻ったとき、やはり合計は0になっているはずだ。電位は、単位電荷当たりのエネルギーだから、これは「エネルギー保存則」なのだろう。
悩ましい問題は、いずれの法則においても対象となるそれぞれ、「枝分かれポイント」、および、「閉回路」の個数なのである。
条件式は「独立」なものでなければ意味がない。しかし、どの「枝分かれポイント」、どの「閉回路」を選べば、「独立」になるかは、それほど自明ではないので、・・・。
ここには、「ケーニッヒスベルグの橋渡り」に遡る、「一筆書き」や「地図の塗り分け」とも関連する、「位相幾何学上」の重要な定理が関係しているはずなのだが、私にはもちろん(笑)、厳密に説明することはできない。
- キルヒホッフ第1法則:「枝分かれポイント」に関しては、全ポイント数から1を引いた個数の条件式が「独立」となる、様である。ここでは、ポイントはa,b,c,d,e、5個あるから、一つ減らして、a,b,c,dの4個について考えることにする。
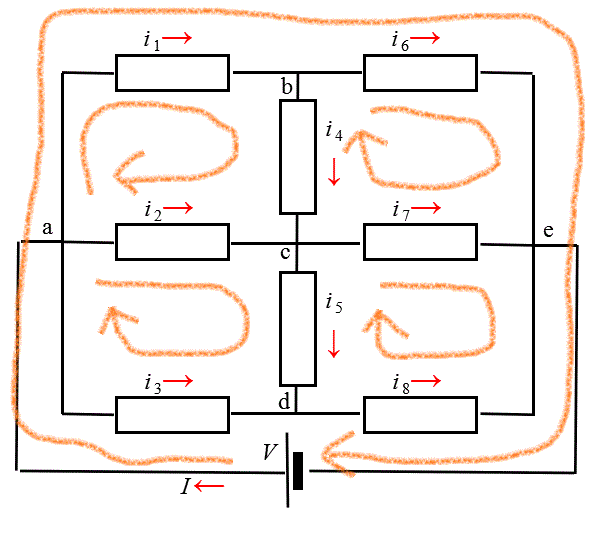
- キルヒホッフ第2法則:「閉回路」はもっと悩ましい。一体この図形に、ある点から出発して線を伝って同じ点に戻ってくることができる、という意味で、(「八の字」型のようなものは、二つの「輪」に還元できるから、含まない、ところを見ると、これも、数学上の「単一閉曲線」の概念に関連があるのだろう)、一体、いくつの「閉回路」が隠されているだろう?、かなり膨大なものになるはずで、そこから「独立」なものを選ぶには、いずれ理論的な裏付けがあるのだが、プラクティカルには(笑)、全部で、9個いるんでしょ?、「第1法則」で4個出たから、あと5個あればいいんでしょ?、ということで、
「abca」、「becb」、「acda」、「cedc」、そして最後に電源Vを絡めて、「VabeV」、の5つを選ぶことにする。
では、始める。
符号を付け替えたり並べ替えたりして整理、通し番号もつける。
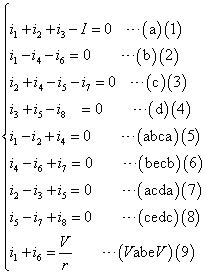
i1を用いて他の変数を表すことを試みる。
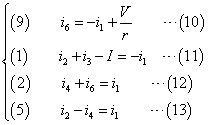
さらに、
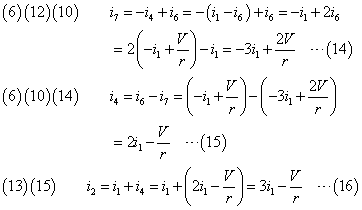
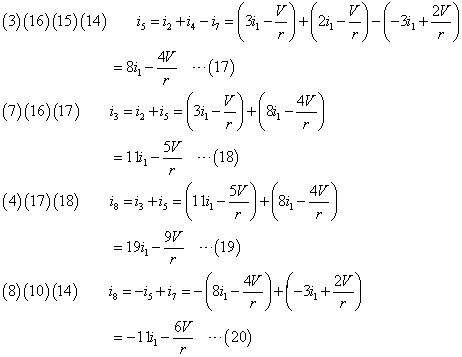
これでつながった!、(19)(20)から、
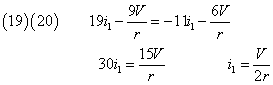
あとは、次々と、
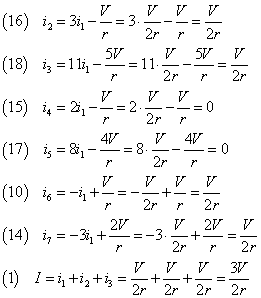
大げさな計算の割には、結果は、ばかばかしい(笑)。すべての抵抗が同じ値だから、図を一瞥して、「入れ替え可能」な変数の組が、いくつもある。
はじめからこの関係を「組み込んで」、あらかじめ変数の数を減らすことも可能であったが、「私」の趣味としては(笑)、「悪い頭」(笑)はなるべく使わず、多分、頭よりは賢い(笑)、「手」を信頼して、「単純作業」に還元したい、と思う。
計算結果は、この関係をちゃんと満たしているから、多分(笑)、合っているのだろう?
i4、と、i5に電流が流れない、という結果は、実は、迂闊にも(笑)「予想外」であった。これは、どういう「意味」なのか?、「解釈」でも加えて見なければ、格好がつかない。
水は低きに流れる、と、同様に、電流は、電位の高いところから低い場所に向かって、流れる。
電流が「流れなかった」、ということは、電位差が「なかった」ことを意味する。つまり、bとc、cとdは、それぞれ、等しい電位なのである。
bc間、cd間、を断線させてみよう。
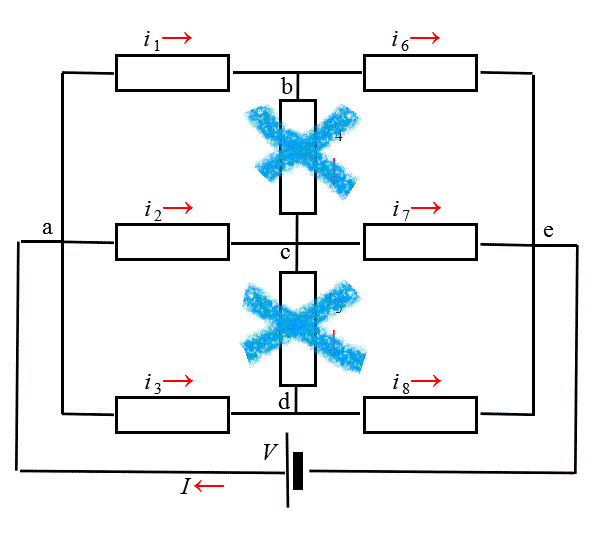
これならば、抵抗値rの二つの抵抗がまず直列接続しているから、r+r=2r、
それが3組、今度は並列接続しているから、合成抵抗Rは、
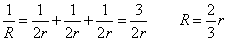
したがって、
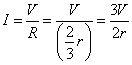
と、当然、合致している。
この状態で、3つの並列な経路、abe、ace、adeは、対等だから、そのそれぞれの中間地点b、c、dは、同電位である。だから、そ・こ・で・、改めて、bc間、cd間を、こっそり(笑)、線でつないでも、電流は流れないのである。
物事の生じた順番は、「現実」とは異なっていても、出来上がった状態が同じだから、だから、同じなんだ(笑)、と言えるのは、実は、不思議なことではあるのだけれど、・・・。