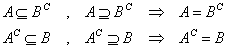「世界」を、二つの問い、「あなたは、Aですか?」、と、「あなたは、Bですか?」に対する答えによって「切り分けると」、か・な・ら・ず・、4つの部分が発生する。
- A∧B、・・・、Aであり、かつ、Bである、▲、
- A∧¬B、・・・、Aであり、かつ、Bでない、▲、
- ¬A∧B、・・・、Aでなく、かつ、Bである、▲、
- ¬A∧¬B、・・・、Aでなく、かつ、Bでない、△、
私たちがしばしば陥る短慮、謬見は、これら、か・な・ら・ず・ありうる4つの部分のうち、一つまたは二つを、「無視できるほど少数だから」と言って、切り捨ててしまうことである。切り捨ててしまうことで、何が起こるか?
これら4つの部分集合のどれか一つを空集合φにしてしまうという変形を加えることによって、そうなると残りは3つの部分集合しかないわけだから、これはおそらく、例の「四色問題」と関係しているに違いないが、「世界」が3つの部分に、「排反的に、かつ、すべてを覆うように」分割されたとき、必ず、どれかがどれかを「包含」する関係が現れ、したがって、いずれの場合も、「条件関係、○○であるならば△△である」、が、発生する。当然、、4C1=4、4つの場合がありうるから、逐次、見てみよう。
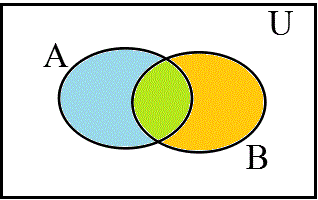
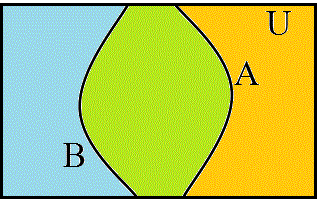
- まず、これが、「世界」の、普通の、あり方。「A∧B、グリーン▲」、「A∧¬B、ブルー▲」、「¬A∧B、オレンジ▲」、「¬A∧¬B、白△」で描かれた4つの領域が存在する。左側の記法、「ベン(Venn)図」というのは、全体集合U(universe)を長方形で表してしまうから、では、その長方形の4辺の「外側」に、何があるのか?、という難問に逢着してしまう。「世界」に「果て」があり、なおかつ困ったところは、その「果て」が、「白」の集合、¬A∧¬B、と「接している」かのごとき錯覚を与えてしまう所が、いけない。世界に「果て」があるかどうか、が問題なのではなく、4つの部分集合は、ぜひとも「対等」でないと、困る、のである。「果て」もなく、どこまでも「対等」であるのは、「陰陽yingyang」のエンブレムが示す如く、無限に循環する三角関数、「円」、でなければならない。私たちが生まれた星が、球体であったのは「偶然」なのだろうか?、球体で「ない」星がありえないなら、私たちが、「無限」を組み込んだ「世界」を構想するとき、「球体」しか思い浮かばないのは、決して「偶然」ではありえない、「所与」の条件だったのでは?、そこで、無限に広がる「xy平面」の各点を、点(0,0,2)と結ぶ線分が、「(0,0,1)を中心とする、半径1の球面」と交差する点と、「1対1対応」をなすことを発見したリーマンの着想にあやかり、「Venn図」の四辺を、ぐにゃりと紙面の裏側に向かって折り返し、一点に結んでしまえば、右側の球ができるであろう?
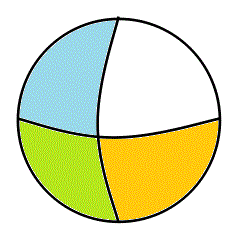
- では、ここから、「i」A∧Bを削除してみると、以下の二つの「包含関係」が発生する。「包含関係」あるところ、かならず、「条件関係」が成立することになる。すなわち、
- A⊂¬B、ここから、A→¬B、「Aであるならば、Bでない」、が帰結する、
- B⊂¬A、ここから、B→¬A、「Bであるならば、Aでない」、が帰結する、
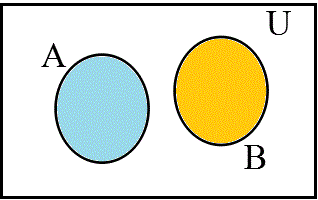
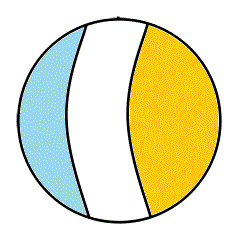
- 同様に、「ii」A∧¬Bを削除してみると、
- A⊂B、ここから、A→B、「Aであるならば、Bである」、が帰結する、
- ¬B⊂¬A、ここから、¬B→¬A、「Bでないならば、Aでない」、が帰結する、
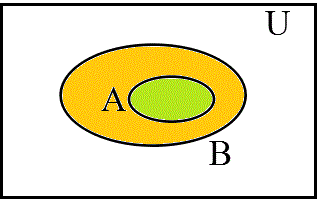
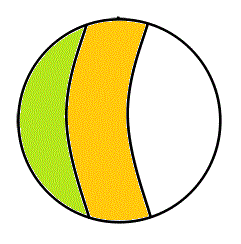
- 「iii」¬A∧Bを削除してみると、
- B⊂A、ここから、B→A、「Bであるならば、Aである」、が帰結する、
- ¬A⊂¬B、ここから、¬A→¬B、「Aでないならば、Bでない」、が帰結する、
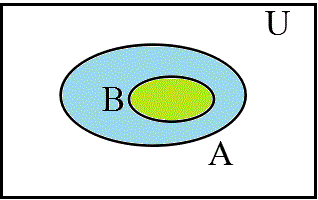

- 最後に、「iv」¬A∧¬Bを削除してみると、
- ¬A⊂B、ここから、¬A→B、「Aでないならば、Bである」、が帰結する、
- ¬B⊂A、ここから、¬B→A、「Bでないならば、Aである」、が帰結する、
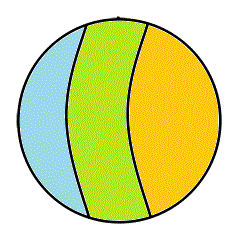
こうして、3つに塗り分けられてしまった「世界」から、さらにもう一つの部分集合を空集合φにしてみよう。結果からいえば(笑)、4つの部分集合から2つを選んで削除するのであるから、4C2=6、6通りありうる。
- これは、「A∧B、グリーン▲」、「A∧¬B、ブルー▲」、がともに失われてしまった「世界」であるから、A=φ、もはや、「あなたはBであるか、Bでないか?」し・か・問われていない。
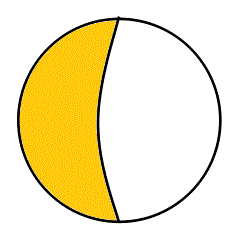
- これは、「A∧B、グリーン▲」、「¬A∧B、オレンジ▲」、がともに失われてしまった「世界」であるから、B=φ、もはや、「あなたはAであるか、Aでないか?」し・か・問われていない。
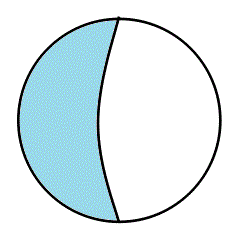
- 次に、「¬A∧B、オレンジ▲」、「¬A∧¬B、白△」、がともに失われてしまった「世界」であるから、¬A=φ、もはや、「世界」はす・べ・て・Aであることは、決まっている、所与の事柄で、あなたは、ただ、「Bであるか、Bでないか?」の問いにし・か・、答えることが、できない。
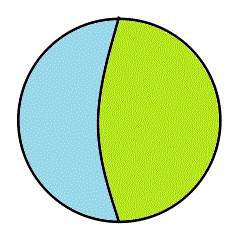
- 「A∧¬B、ブルー▲」、「¬A∧¬B、白△」、がともに失われてしまった「世界」であるから、¬B=φ、もはや、「世界」はす・べ・て・Bであることは、決まっている、所与の事柄で、あなたは、ただ、「Aであるか、Aでないか?」の問いにし・か・、答えることが、できない。
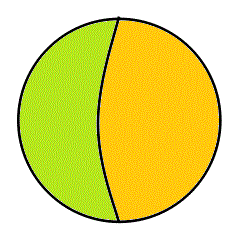
- 「A∧¬B、ブルー▲」、「¬A∧B、オレンジ▲」、がともに失われてしまった「世界」であるから、これは、A=B、AであることがBであるための必要かつ十分条件である、AとBは同値である、ことになり、二つの問いは、実は、一つの問いでしかなかった、あなたは、ただ、「AすなわちBであるか、AすなわちBでないか?」の、やはり一つの問いにし・か・、答えることが、できない。
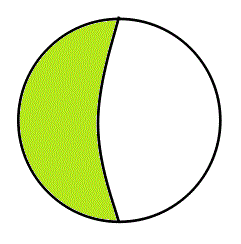
- 最後に、「A∧B、グリーン▲」、「¬A∧¬B、白△」、がともに失われてしまった「世界」であるから、これは、「AとBが排反で、かつ、すべてを覆っている」状態である。¬A=B、A=¬Bと言ってもよい。ここでは、Aでなければ「自動的に」Bであり、また、Bでなければ「自動的に」Aなのである。「あなたはAであるか」との問いに続けて、「あなたはBであるか」と、問う「必要が」、もはや、ない「世界」である。
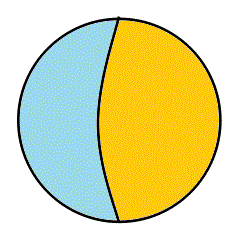
短慮、謬見は、主に二つの場面で起こりうる。
- AとBが、「対概念」をなしている、と思われる場面。Aに「男」、Bに「女」、または、Aに「国民」、Bに「外国人」、を、代入してみよ。
自分を「男」でも「女」でもある、と感じている者と、自分を「男」でも「女」でもない、と感じている者とが、か・な・ら・ず・、存在する。
誰が「国民」であるかは国家が決定する、という。国税の納付義務があるか、国民健康保険の受給資格があるか、選挙権があるか、すべて異なる国法が決定する。ならば、「国民」の定義は、準拠法によって異なるのである。「外国人」であることが、かりに、「○○国」の旅券を発給されうるもの、と一元的に定義してみたところで、「国民であって、外国人であるもの」、「国民でなく、外国人でもないもの」が、発生するのを止めることはできない。
- もう一つは、AとBが、「類義語」、常識的には、ほぼ同じ範囲をカバーしている、と感じられている場合。
さしあたり、穏当に、Aに「年金生活者」、Bに「65歳以上」、を代入してみよ。それでも、65歳未満で年金支給を受ける場合があり、また、65歳を過ぎても、年金支給がない(笑)者も、ちゃんと存在するのである。
Aに「共産主義者」、Bに「非国民」、を代入してみよ。
Aに「○○教徒」、Bに「テロリスト」、を代入してみよ。
もちろん、前回からの話のつながりは、ここにあった。「共産主義者は非国民Un-Americanである」という言明の「非論理性」を、そうね(笑)、きっと「構造主義的」に(笑)、証明してみせたことには、なっていると、思う。
前回、図を掲げて、そりゃ、絵を見りゃ、当然だろ?、みたいな議論を進めたが、それは、なんだか「数学的」な「厳密さ」を欠くような気がして、気の弱い私は不安で(笑)、一応、「証明」という形を取ってみたくなった。もちろん、閑人の手遊び(てすさび)である。
「証明」の前提、として、以下の基本定理はすでに証明され(笑)、ているものとする。「確率論入門」赤摂也(ちくま学芸文庫)、による。
- 「定理1」は、和集合(結び)、に関するもの。iは交換法則、iiは結合法則、iii、iv、vは包含関係に関するもの、vi、viiはそれぞれ空集合と、全体集合に関するもの。同書では、包含関係に等号を含む形の記号が用いられ、また、全体集合をΩ(オメガ)で、補集合は、右肩にcomplementの「C」を置くことで、表している。それぞれの記法の流儀には、何か意味があるに違いないが、改変する自信がない(笑)、ので、そのままにしておく。
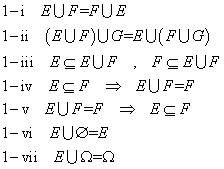
- 「定理2」は、同様に、積集合(交わり)、に関するもの。
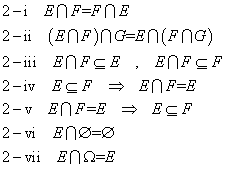
- 「定理3」は、和と積についての、分配法則。
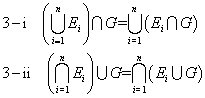
- 「定理4」は、補集合に関するもの。
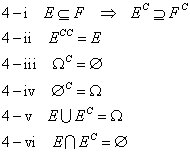
- そして、「定理5」は、「ド・モルガンの法則」。
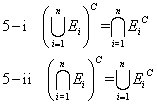
では、やってみる。うまくいきますかどうか?、ばかばかしい、うまくいったからこそ、得意そうに書いているに決まっている。
- これが、普通の、状態。ここには包含関係はないから、証明すべきことが、ない。

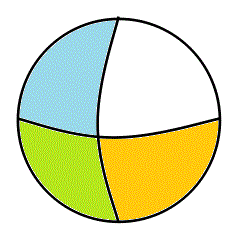
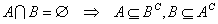 を、示したい。右側に赤字で示したのは、上の定理の番号、*は、与えられた条件式。
を、示したい。右側に赤字で示したのは、上の定理の番号、*は、与えられた条件式。
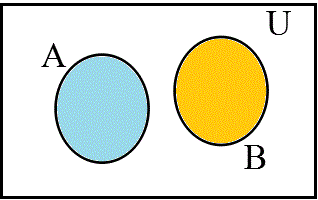
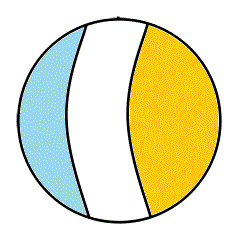
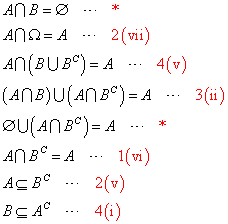
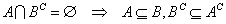 を、示したい。
を、示したい。

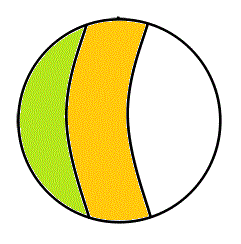
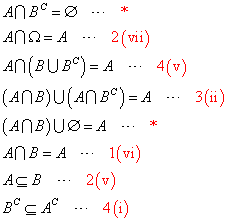
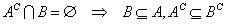 を、示したい。
を、示したい。


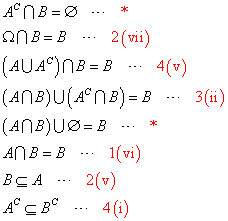
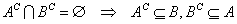 を、示したい。
を、示したい。

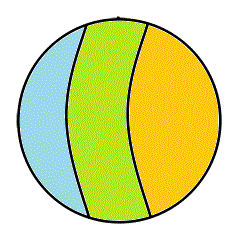
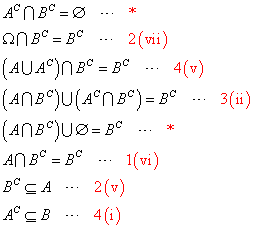
次に四つの部分集合のうち、二つを空集合にしてしまった場合。
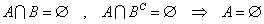 を、示したい。
を、示したい。

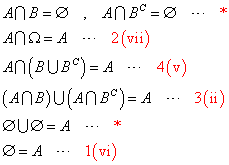
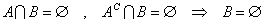 を、示したい。
を、示したい。

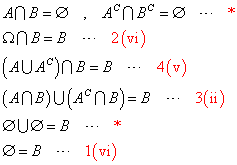
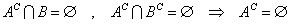 を、示したい。
を、示したい。
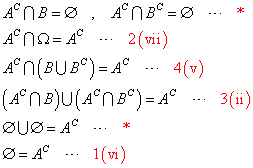
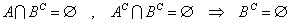 を、示したい。
を、示したい。
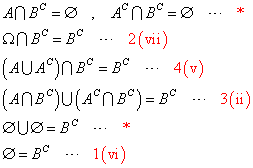
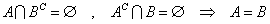 を、示したい。
を、示したい。

これはちょっと悩ましく、ほかの方法もあるはずだが、苦し紛れ、
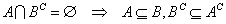
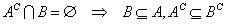
が既に示されているから、
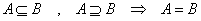
そんな「定理」、上にないじゃない?、ということだが、とりあえず、こうしておく(笑)。
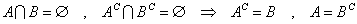 を、示したい。
を、示したい。
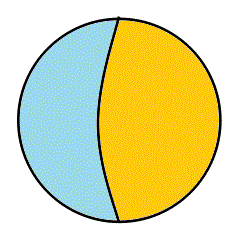
同様に、
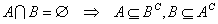
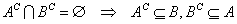
が既に示されているから、
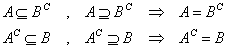

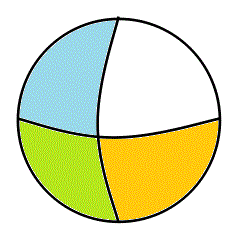
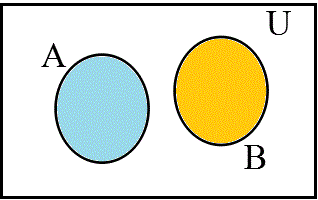
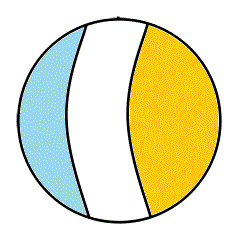

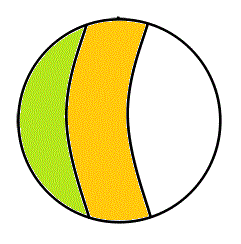



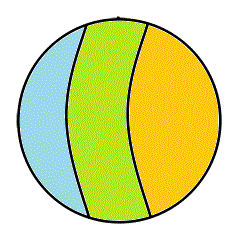


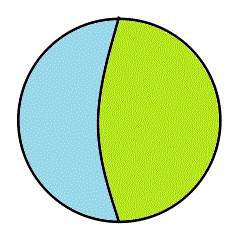
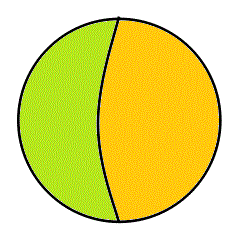

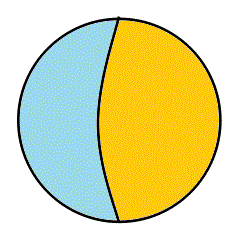
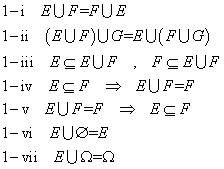
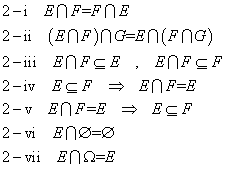
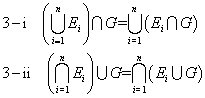
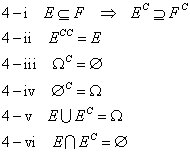
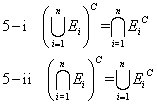
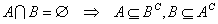 を、示したい。右側に赤字で示したのは、上の定理の番号、*は、与えられた条件式。
を、示したい。右側に赤字で示したのは、上の定理の番号、*は、与えられた条件式。
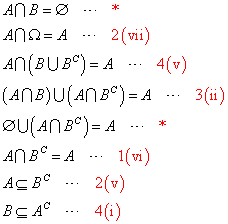
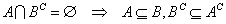 を、示したい。
を、示したい。
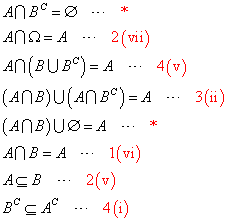
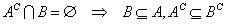 を、示したい。
を、示したい。
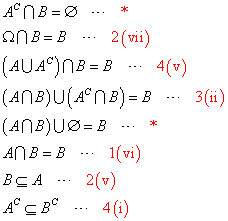
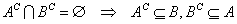 を、示したい。
を、示したい。
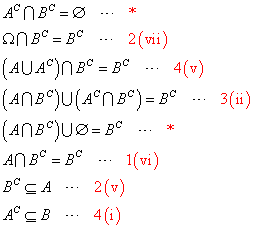
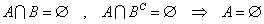 を、示したい。
を、示したい。
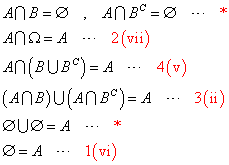
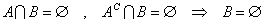 を、示したい。
を、示したい。
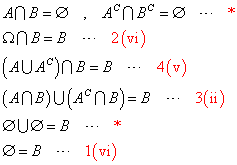
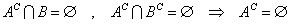 を、示したい。
を、示したい。
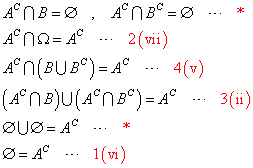
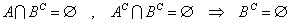 を、示したい。
を、示したい。
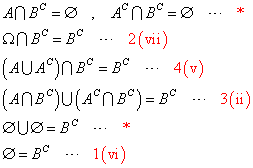
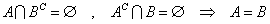 を、示したい。
を、示したい。
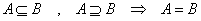
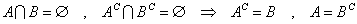 を、示したい。
を、示したい。