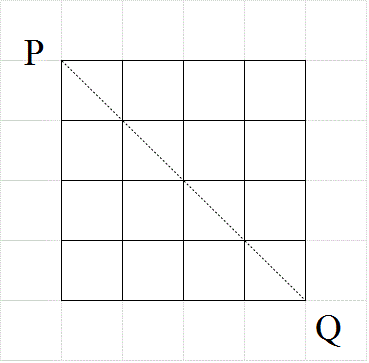
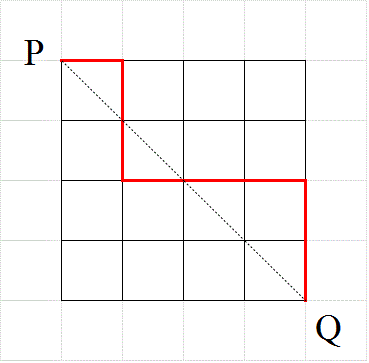
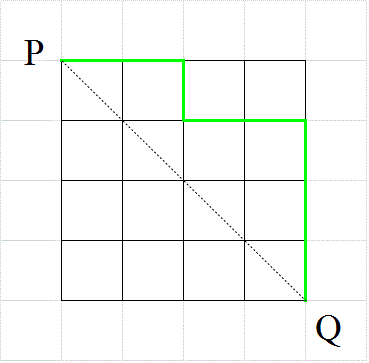
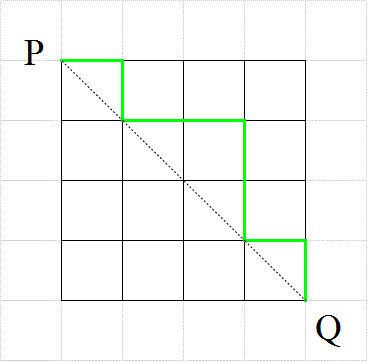
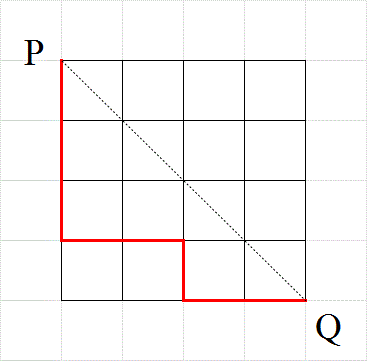
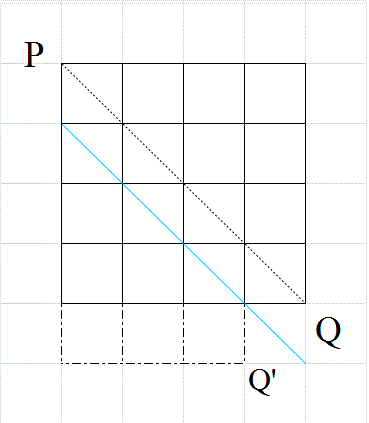
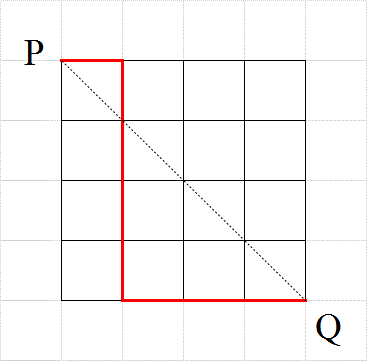
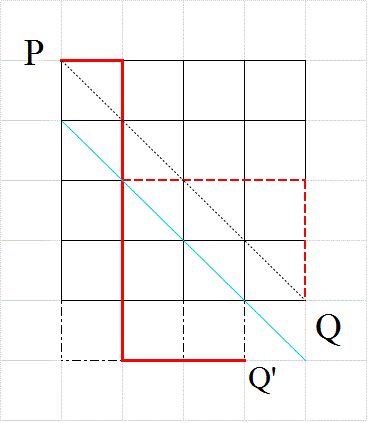
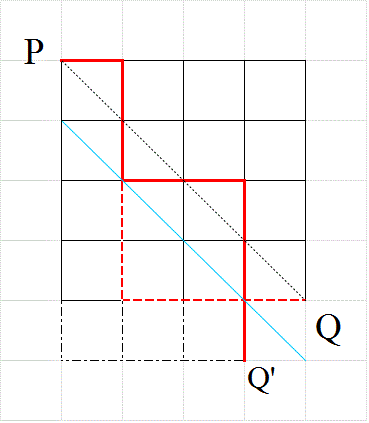
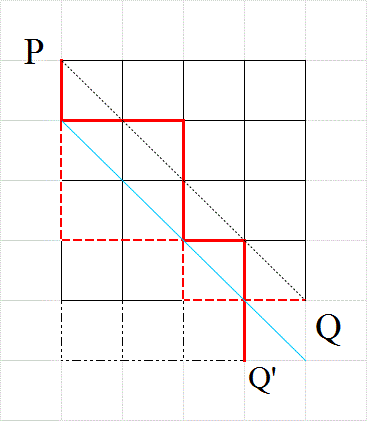
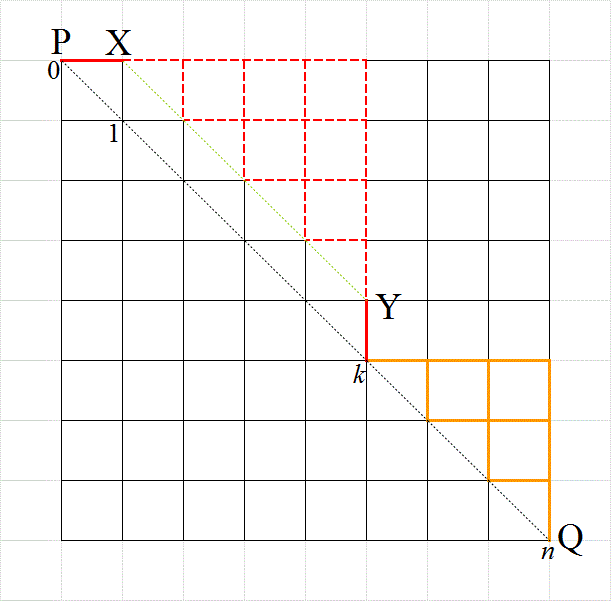
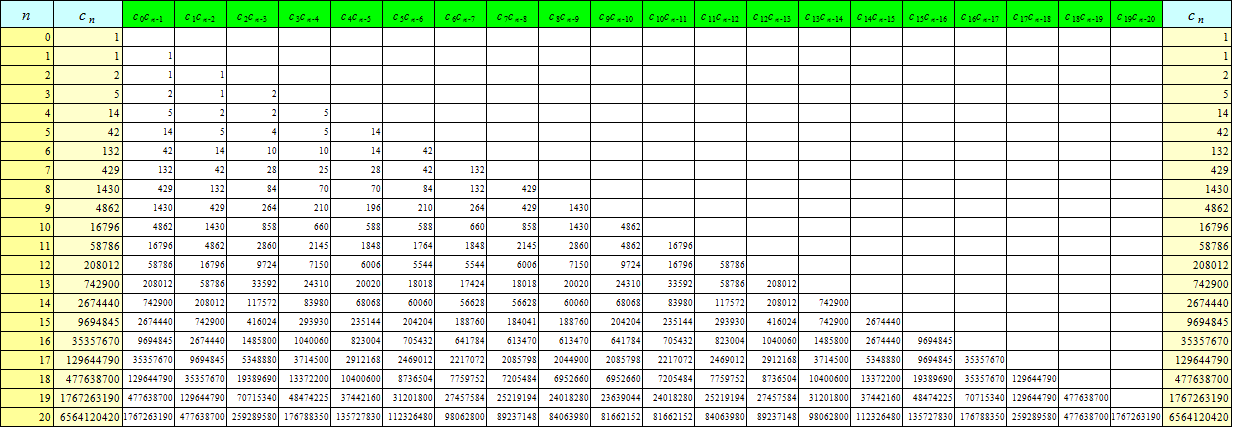
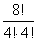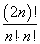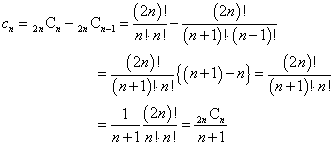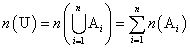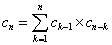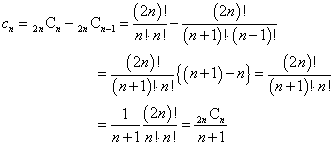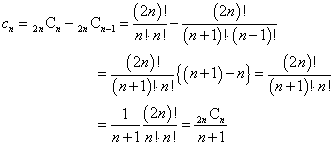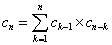- 一辺nの正方形の格子の、上半分しか使ってはならない、という「制限付きの最短経路」問題においては、
対角線PQ上の、P以外のどの点をは・じ・め・て・通過するか?、が、有効な「直和分解」となった。
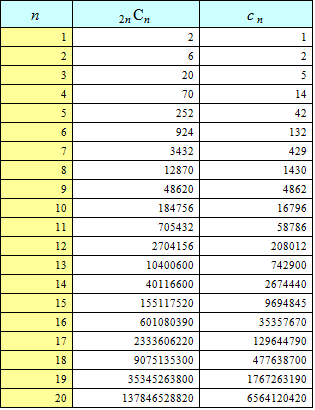
そして、そのすべての場合の数は、cnで表された。
- m語の「構文分析」においては、
m語の「間」の、m-1か所の、どこに第・1・段・階・の・仕切りを入れるか?、が、有効な「直和分解」となる。
そして、そのすべての場合の数は、cm-1で表されることになる。
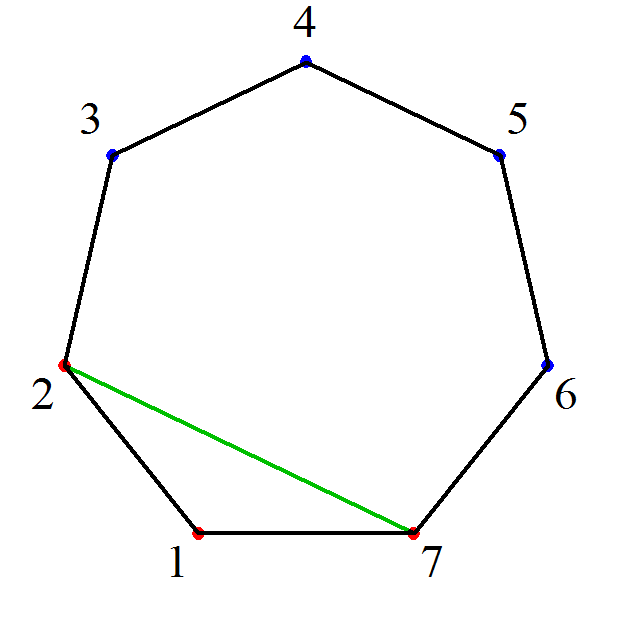
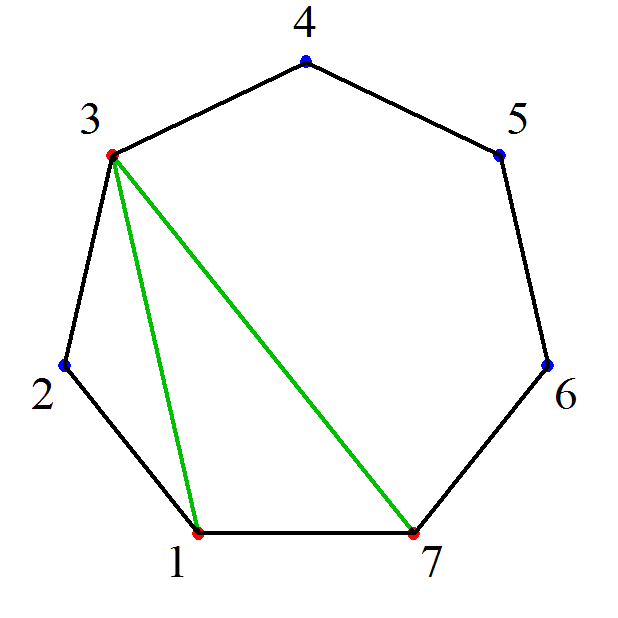
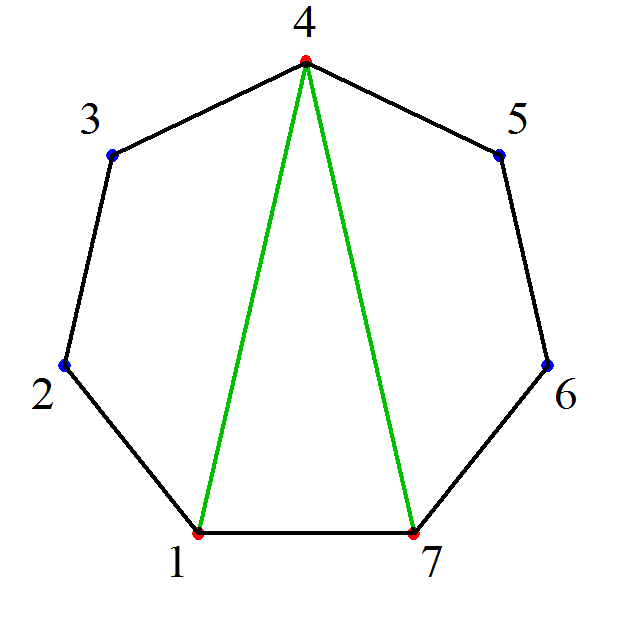
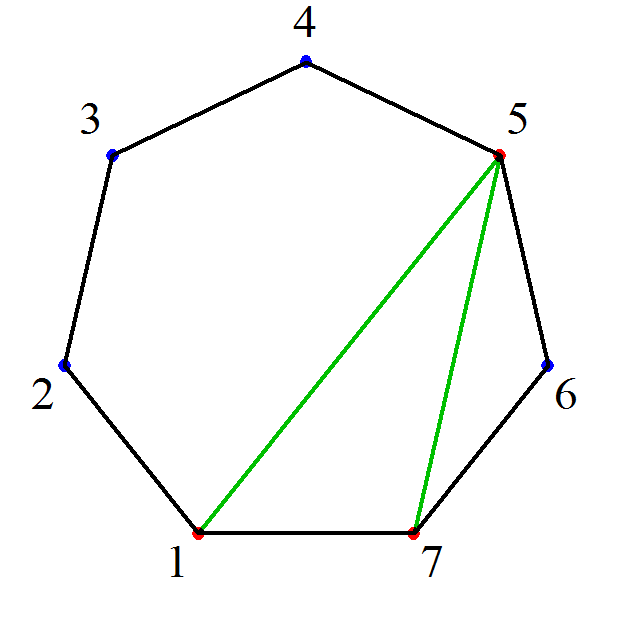
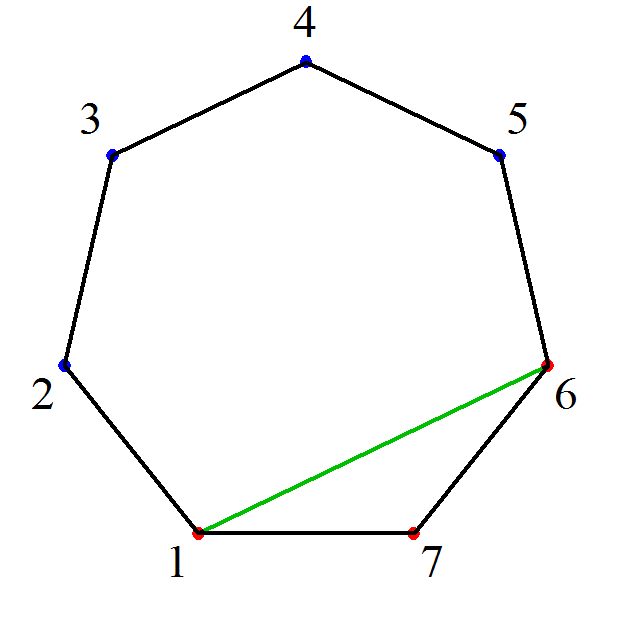
- 「凸l角形の三角形分解」においては、
l個の頂点のうち2頂点を底辺として固定するから、残りl-2個のうち、その底辺と三角形をなしうる、も・う・一・つ・の・頂点をどれにするか?、が、有効な「直和分解」となる。
そして、そのすべての場合の数は、cl-2で表されることになる。
|