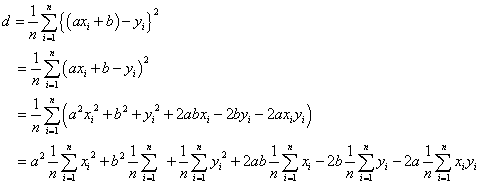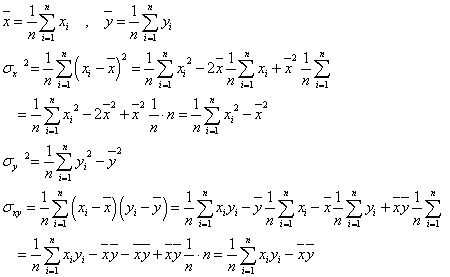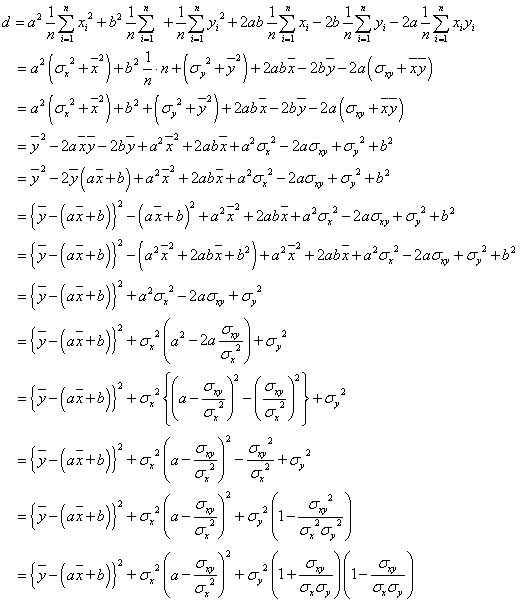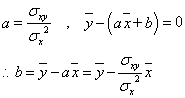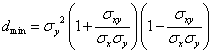2変量(x_i,y_i)、だたしi=1,2,3,・・・,n、に対して、これらを、xy平面上のn個の点とみなしたとき、これらの点との距離の総和が、最も小さくなる直線y=ax+bが、ただ一つ見つかるはずである。これを、これら2変量データの「回帰直線」と呼ぶ。ただし、実際に「距離」を計算するのは煩雑であるから、データx_iに対応する直線上の点のy座標ax_i+bと、実際のデータy_iとの差の二乗をn個のデータについて足し合わせたものの平均値dについて考えることにする。すなわち、

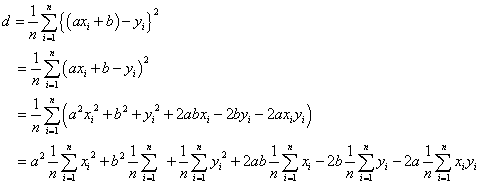
ここで、平均、分散、共分散の定義から、

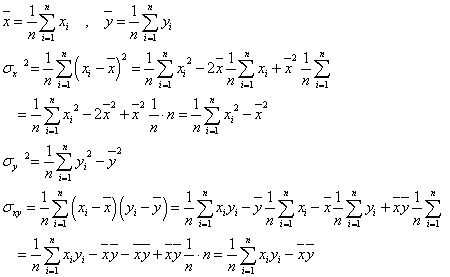
つまり、手短に言うと、「分散」は「二乗の平均から平均の二乗を引いたもの」、「共分散」は「積の平均から平均の積を引いたもの」、である。これらを用いて、

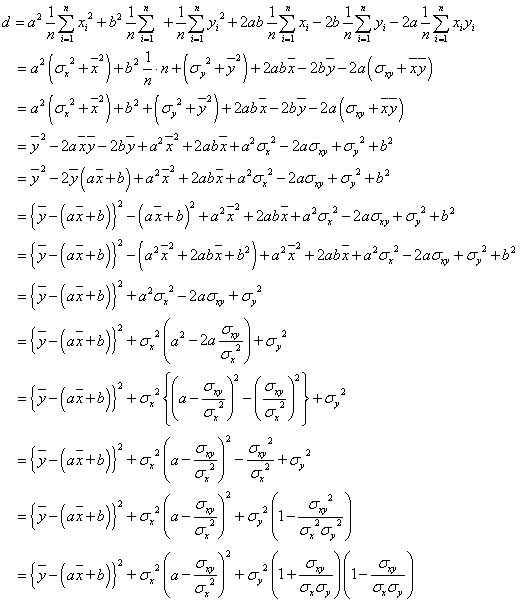
これで出来上がりですね。「平方完成」を2回行っている形なのですが、第1項、第2項がともに0になるとき、この式は最小値を示すであろう、第1項の方は、理想的な「回帰直線」が得られたなら、当然、(xの平均値,yの平均値)もそこに乗っかっているはずだろう、という推定にもとづいているんだろうと思われます。第2項が0になるような値として、a=σ_xy/σ_x²と、こうして「回帰直線」の傾きが定まり、引き続いて、第1項も同時に0である、という条件から、その「y切片」bも定まることになるだろう、すなわち、

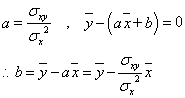
こうして定まった、回帰係数a,bに対しては、前2項は0になりますから、その残余、これをd_minと呼ぶことにすると、

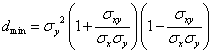
なるほど、ここで、r=σ_xy/σ_xσ_yと定義すれば、
d_min=-σ_y²(r+1)(r-1)

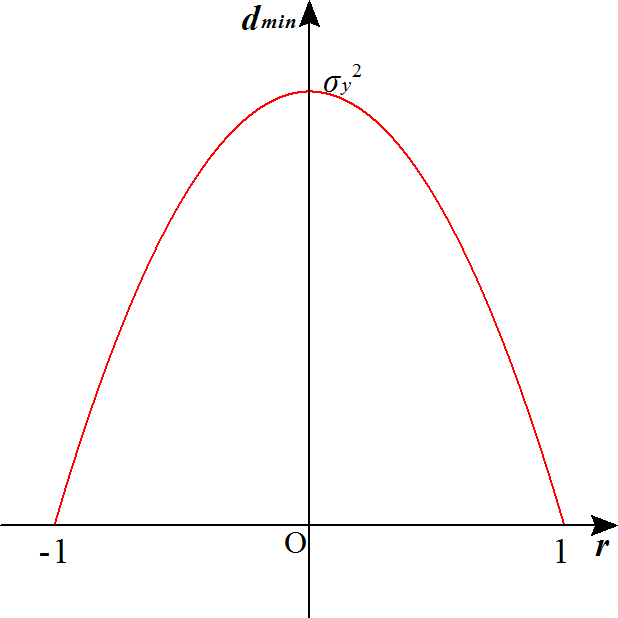
まことに、これぞ「相関係数」、「回帰直線」との隔たりが最も小さくなるのが、r=±1、それぞれ、最も大きくなるのが、r=0、と理解されます。rの符号は、共分散σ_xyの符号と同じだから、それは、相関の正・負、を表すことになる。