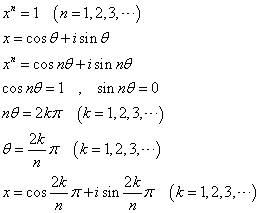
n=2
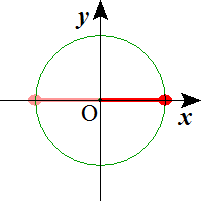 n=3
n=3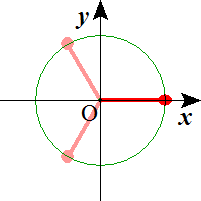 n=4
n=4 n=5
n=5
n=6
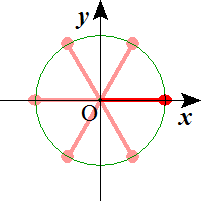 n=7
n=7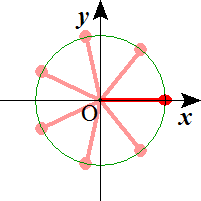 n=8
n=8 n=9
n=9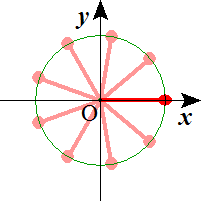
つねに実数1を解にもつ。nが奇数の場合は実数解は1のみであり、nが偶数の場合は実数解は1及び-1である。
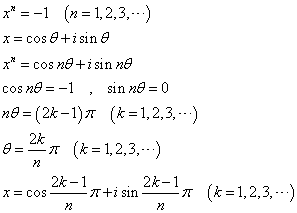
n=2
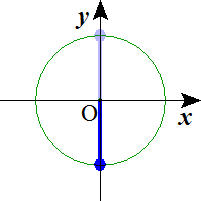 n=3
n=3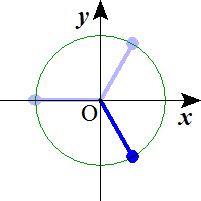 n=4
n=4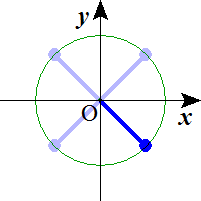 n=5
n=5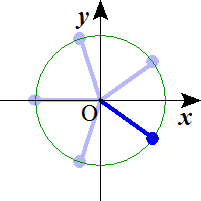
n=6
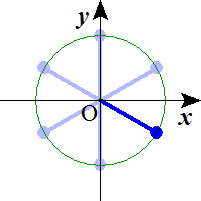 n=7
n=7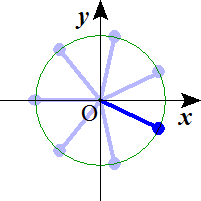 n=8
n=8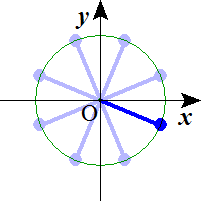 n=9
n=9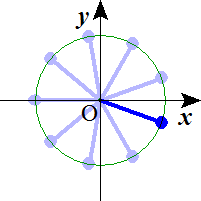
つねに実数解をもつとはいえない。nが奇数の場合は実数解-1をもつが、nが偶数の場合は実数解をもたない。
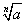 なる表記が、一意的であるためには、次のように定義せざるを得ないだろう。
なる表記が、一意的であるためには、次のように定義せざるを得ないだろう。
- a≧0でなければならない。
- xn=a (ただしa>0) には二つの実数解があるが、そのうちの正のものを採用する。
a=0ならば、この数は0を表す。
- a>0ならば、xn=a には二つの実数解があるが、そのうちの正のものを採用する。
- a=0ならば、この数は0を表す。
- a<0ならば、この表記はnが奇数のときのみ意味をもち、
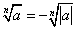 とする。
とする。
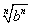 なる表記は何を意味するか?
なる表記は何を意味するか?
- nが偶数ならば、bの正負にかかわらずbn≧0であるから、
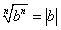
- nが奇数ならば、
- b>0のとき、bn>0、したがって
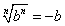
- b<0のとき、bn<0、したがって
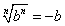
- b>0のとき、bn>0、したがって
- つまり、いずれの場合も、
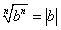 で差支えないことがわかった。
で差支えないことがわかった。