旧暦三月三日は「浜下り」と呼ばれる。「三日月」の日であるから、干潮は正午から、二時間ばかり過ぎた頃になろう、大きく干上がった干瀬に出掛け、潮干狩りなどを行う行事のようである。確かに良く引いている。露頭したリーフエッジまで、歩いていけそうなのだが、比較の対象がないので距離が読めない、だからこんなことを考えた(笑)。
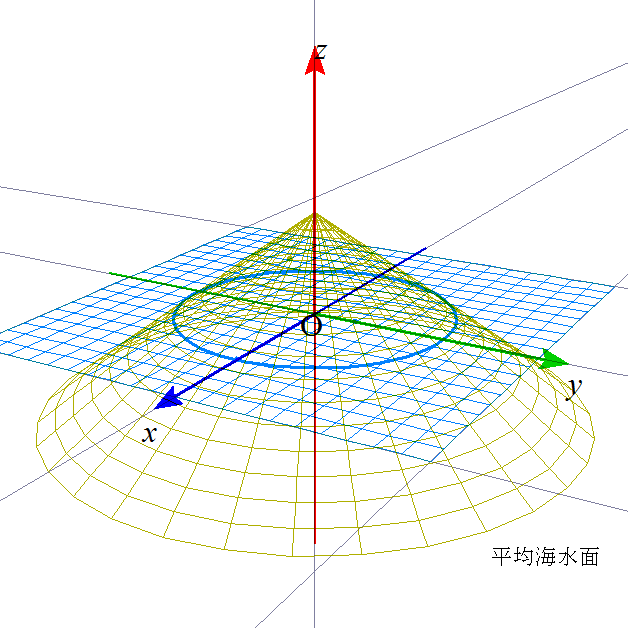
沖縄本島の、少なくとも南部は、隆起サンゴ礁によってできたと言われている。隆起と沈降の繰り返しがあり、その間の時間、浅くて太陽光の通りやすい海にサンゴが造礁した、だから、それは当然、不連続面となるのだが、思い切って(笑)、円錐や四角錐で「近似」してみたらどうだろう？


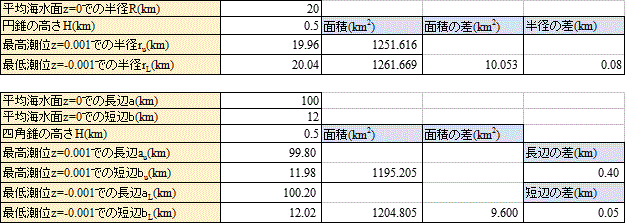
沖縄本島の面積は、約1200平方キロ、これを円形と見做せば、その半径は約20キロ、図中緑で示した。
南西から北東に配置するかなり細長い長方形の方が実情に近かろう、北端の辺戸岬（へどみさき）から南端の喜屋武岬（きゃんみさき）までおよそ100キロ、面積を固定して考えると、横幅は12キロとなろう。図中赤で示した長方形。
錐体の高さをどうするか？沖縄本島最高峰は、国頭村の与那覇岳、約500メートル。隆起サンゴ礁とは異なる北部高島地形であるから、決して島の真ん中にあるわけではないが、ここでは、「直」円錐、「直」四角錐、とすることにした。
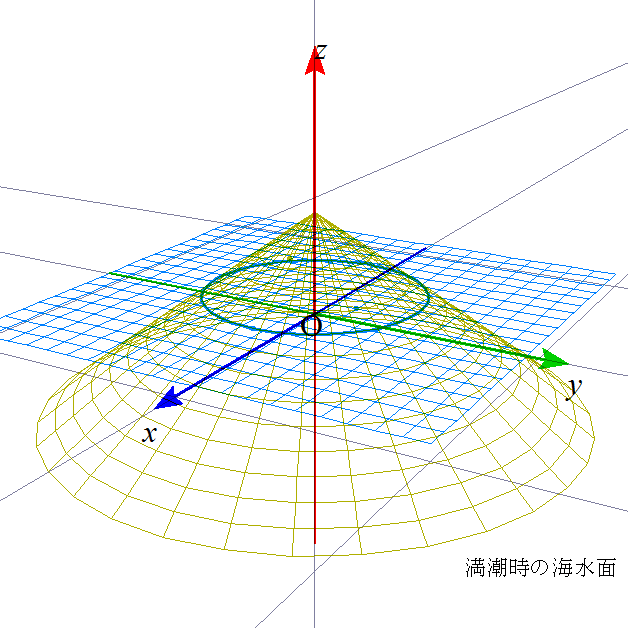
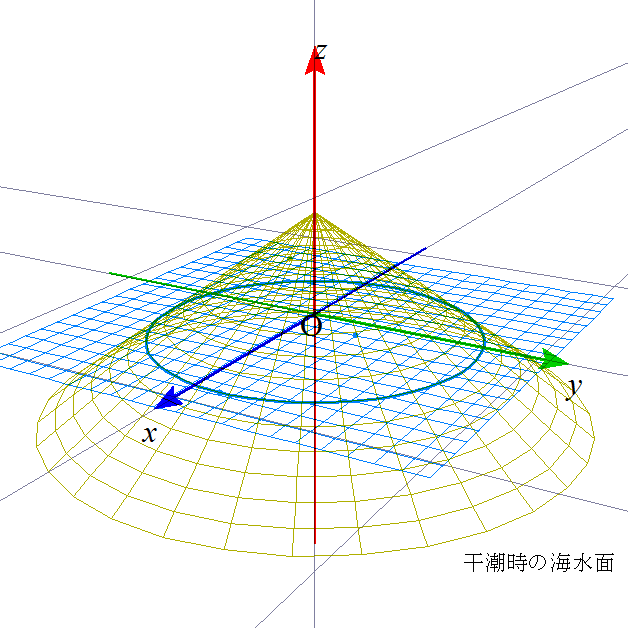
本年の「浜下り」、旧三月三日の潮位は、平均海水面から見て、満潮時プラス76センチ、干潮時マイナス120センチ、とのこと。島の「面積」は当然、平均海水面で測定されているものなんだろうな？だから、ここでは、円錐なり四角錐が、上下1メートルずつ浮んだり沈んだりすることで、水面に現れている部分の面積が、どのくらい変動するものかを調べてみたかったのである。あの見遥かす干瀬の広がりを、数字に表してみたかったのだな。



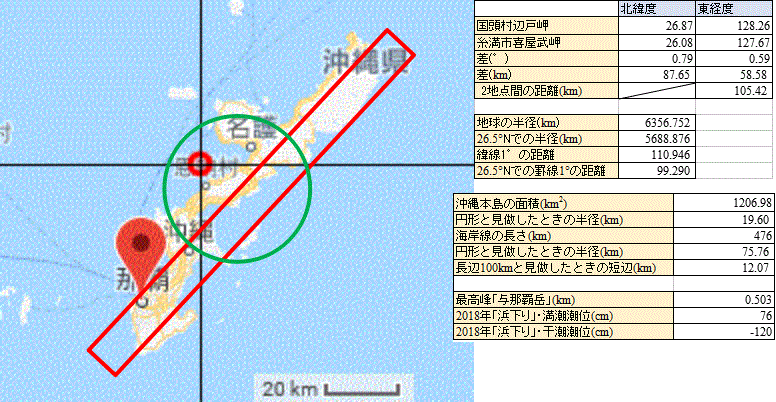
結論は、なかなか凡庸なものである(笑)。島全体で、この日の満潮と干潮とで、約10平方キロの面積が変わる。1パーセント弱だな。それを距離で見ると、円錐モデルでは、80メートル、四角錐モデルでは、長いところで400メートル、短いところは50メートル、まずは妥当なところだろう(笑)、この程度の精度なら、目測で出も言えただろう(笑)、とはいえ、「裏付け」というものがあれば、それはそれで、「心強い」、誰も聞いてくれないが(笑)、自慢そうに語る薀蓄のネタができたわけであった。