半径Rの球面上の点を表すベクトルを、aとすると、その成分表示は、極座標では、
a=(R,θ,φ)
ここに、θは「北極」すなわちz軸と当該点がなす角、「緯度」の「余角」、
φは「赤道面」の大円が0°の「経線」に向けて原点から引いた軸すなわちx軸と、当該ベクトルを「赤道面」に投影したベクトルのなす角、「経度」そのものと言ってよい。

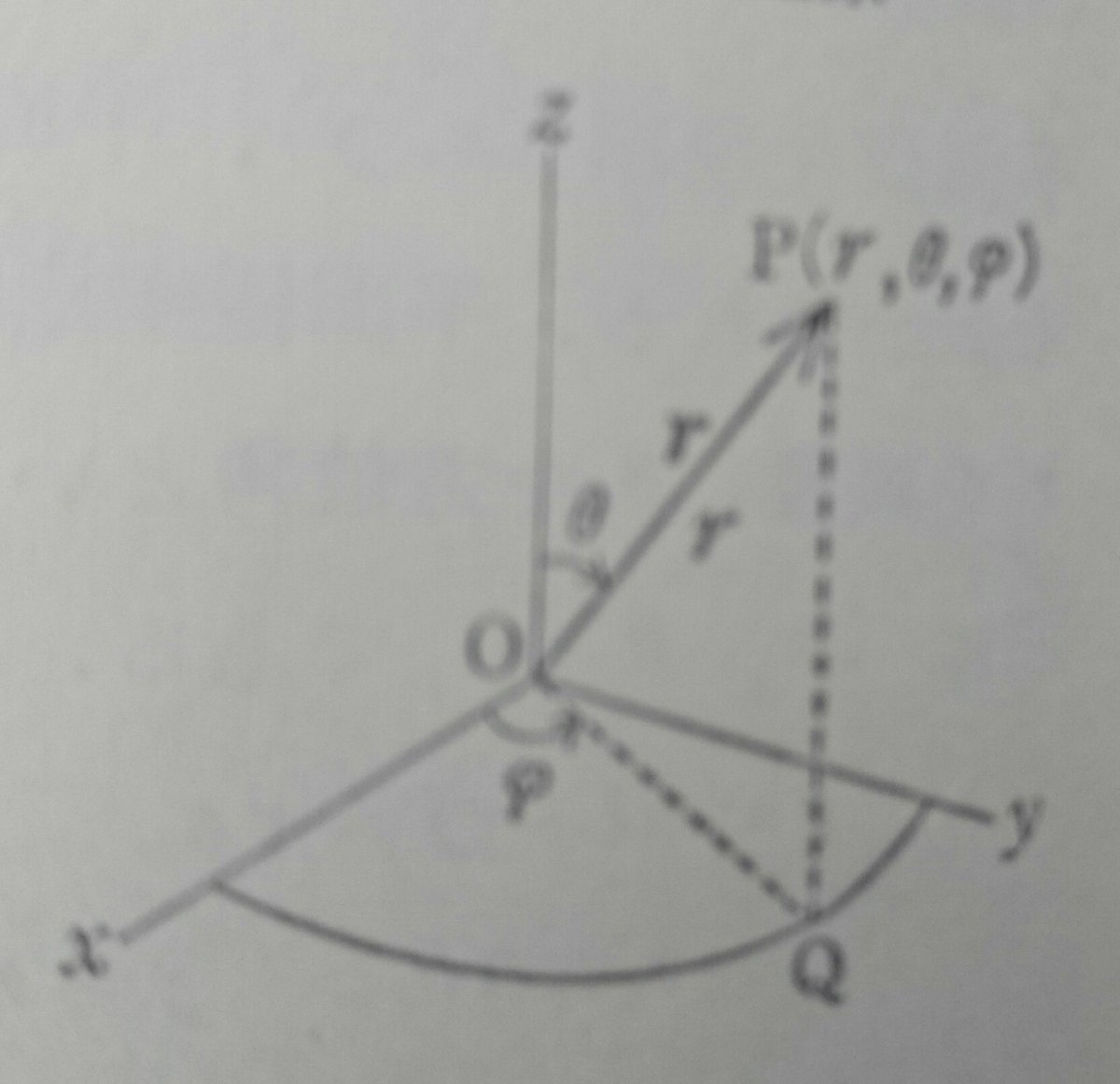
このベクトルの直交座標表示、
a=(x,y,z)
に対して、相互の変換は、
x=Rsinθcosφ
y=Rsinθsinφ
z=Rcosθ
で、定められる。いま、同じく半径Rの球面上の2点を表すベクトルを、a,bとし、それぞれの極座標表示と直交座標表示を、
a=(R,θ1,φ1)⇔a=(x1,y1,z1)
b=(R,θ2,φ2)⇔b=(x2,y2,z2)
とすると、相互の関係はつぎのようになる。
x1=Rsinθ1cosφ1
y1=Rsinθ1sinφ1
z1=Rcosθ1
x2=Rsinθ2cosφ2
y2=Rsinθ2sinφ2
z2=Rcosθ2
すなわち、直交座標表示では、次のようになる。
a=(Rsinθ1cosφ1,Rsinθ1sinφ1,Rcosθ1)
b=(Rsinθ2cosφ2,Rsinθ2sinφ2,Rcosθ2)
ところで、内積（スカラー積）の定義から、2点のなす角をδとすれば、
a・b=|a||b|cosδ
x1x2+y1y2+z1z2=|a||b|cosδ
したがって、ここでは、
Rsinθ1cosφ1Rsinθ2cosφ2+Rsinθ1sinφ1Rsinθ2sinφ2+Rcosθ1Rcosθ2=R2cosδ
両辺をR2で除して、
sinθ1cosφ1sinθ2cosφ2+sinθ1sinφ1sinθ2sinφ2+cosθ1cosθ2=cosδ
従って球面上の2点を表すベクトルのなす角は、
δ=cos-1(sinθ1cosφ1sinθ2cosφ2+sinθ1sinφ1sinθ2sinφ2+cosθ1cosθ2)
こうして当該2点を通る大円の弧長Lが得られた。
L=Rδ