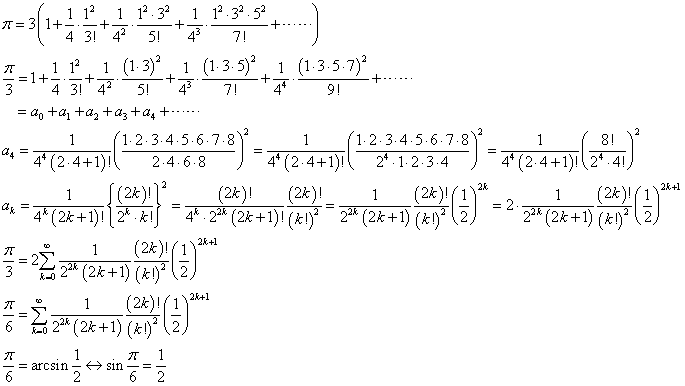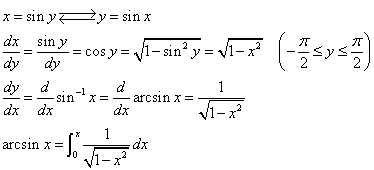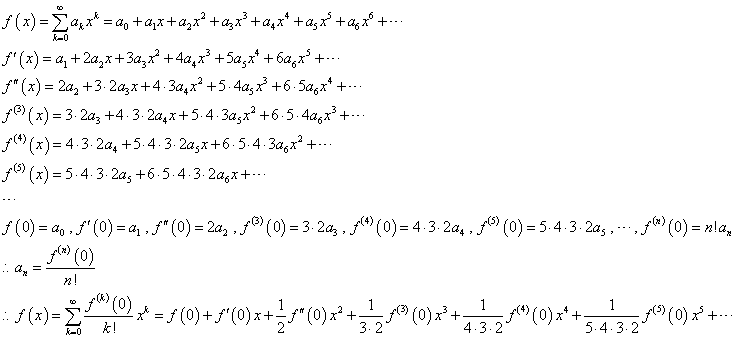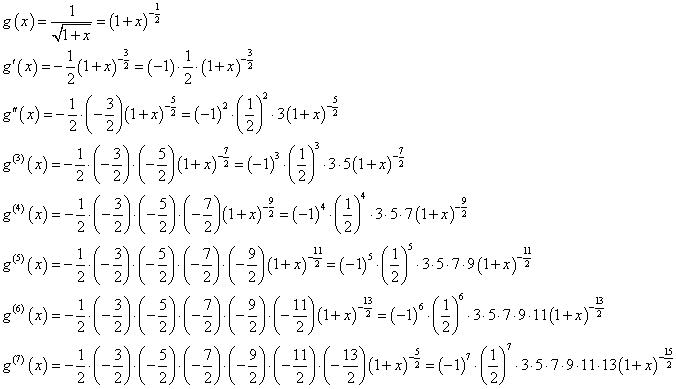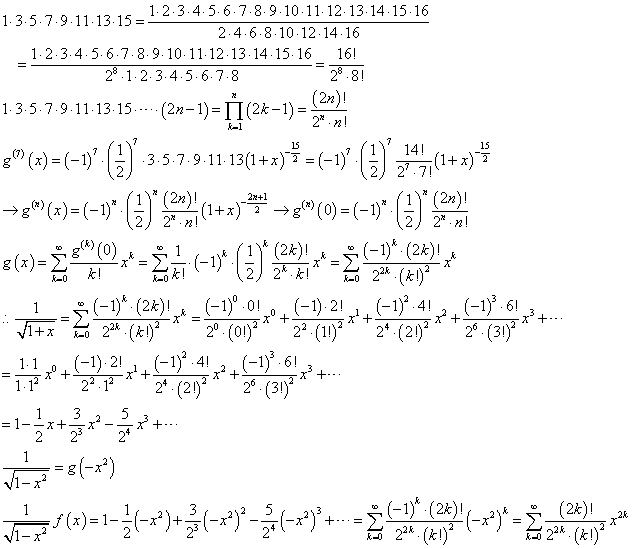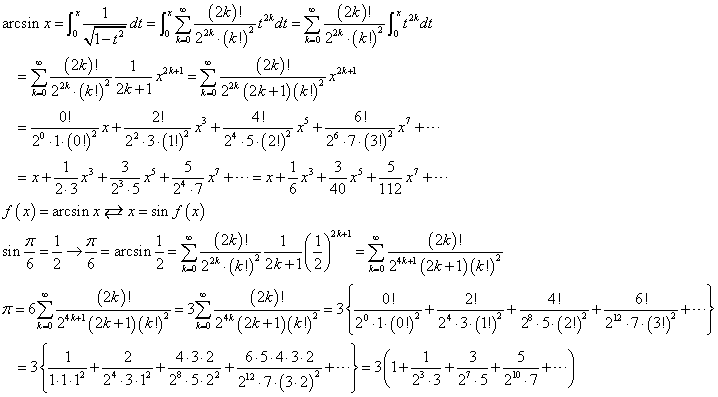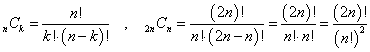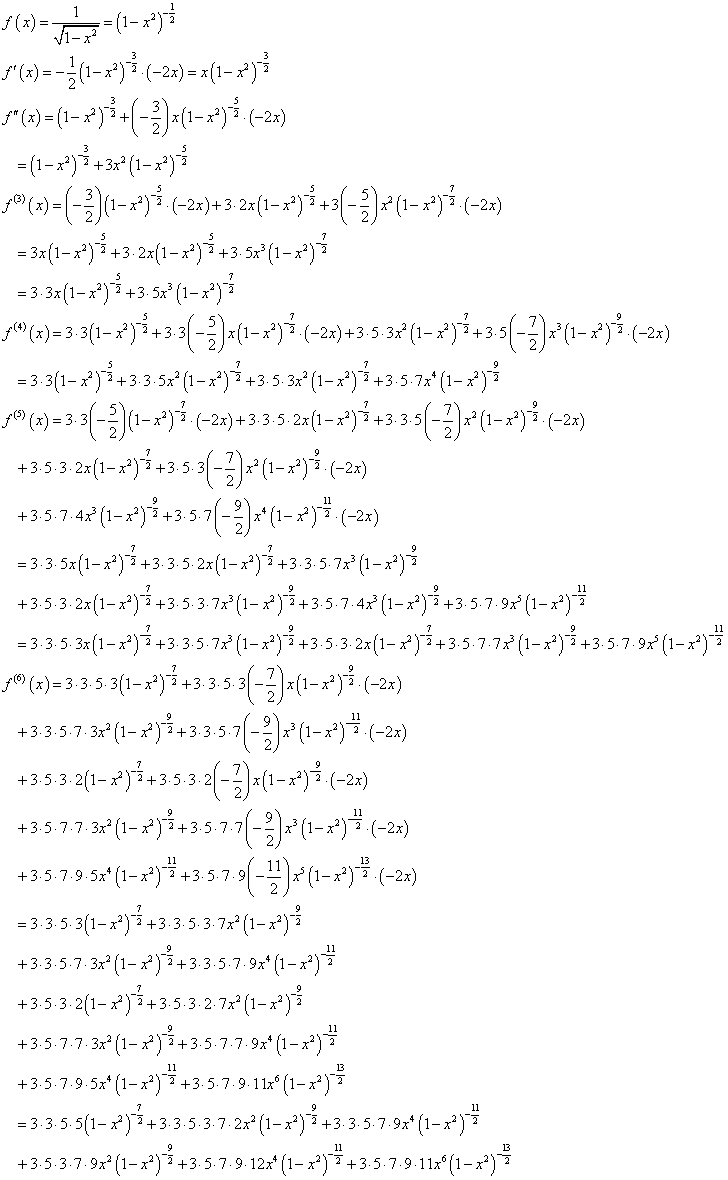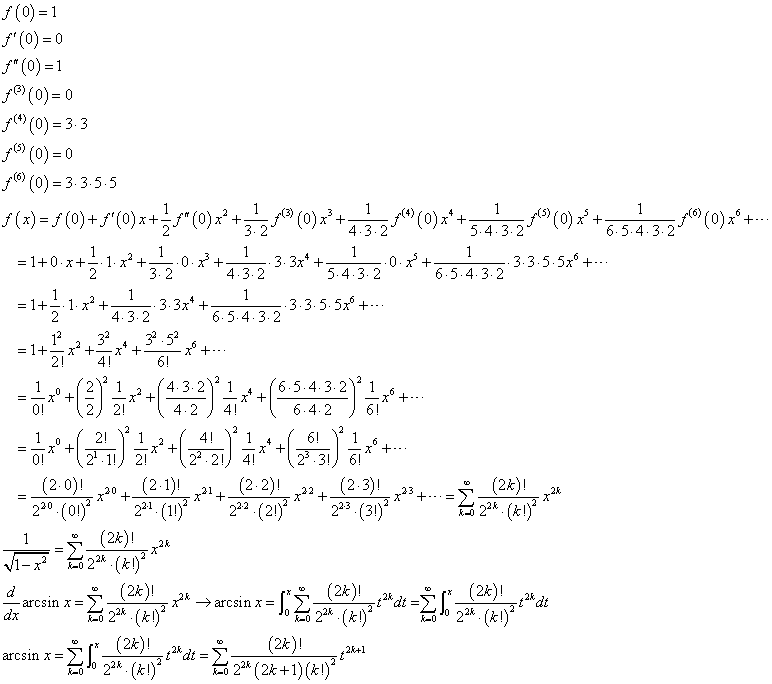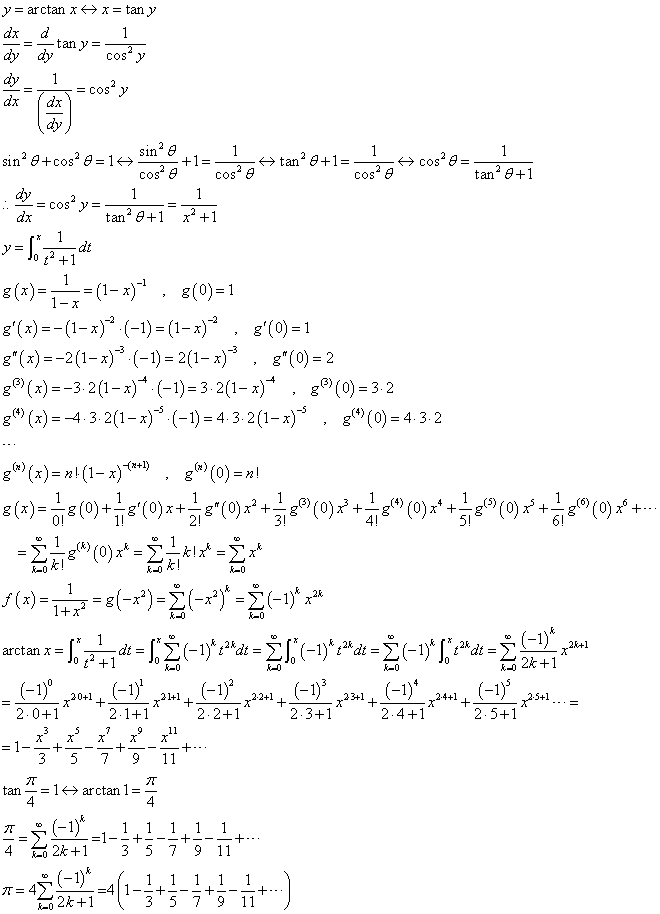「算法少女」遠藤寛子(ちくま学芸文庫)には、あきがオランダの数学書を見せてもらう場面があって、この書物でただ一か所、横書きになった数式が登場します。これがそれなんだが、このままでは、やや法則性がつかみにくいので、項の番号を、最初から、0,1,2,3,・・・、と振ることにしてその五番目、つまりa4を取り出してみましょう。
1・3・5・7は、奇数ばかりを取り出した掛け算ですが、これを「階乗!」の記号を使ってどう表記するか、と言うと、穿った見方ですが(笑)、これは、1から8までの自然数を全部掛けたのち、偶数の2・4・6・8で割ったのだ、と言えばよろしい。
2・4・6・8=24・1・2・3・4=24・4!と、階乗と累乗の記号で書けますから、こうして、一般項の表記ができる。もちろん、きっと、のちに述べる、既に準備した、逆正弦関数の級数展開と関連付けられて欲しい(笑)、と願いつつ変形すると、あらら、確かに、辻褄が合った訳です。
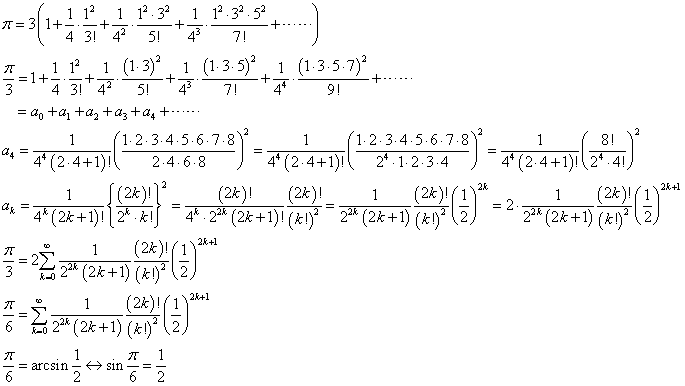
sin(π/6)=1/2、ということは、aracsin(1/2)=π/6、ならば、aracsinxの級数展開式のxには、1/2を代入したうえ、それを6倍すれば、πになる、という仕掛けでした。
では、話は前後しますが、逆正弦関数arcsinxの「べき級数展開」が、どうしてそんな形になるのか、説明させていただきましょう(笑)、いや誰も聞いていないのは知っているが、説明し・た・い・のです。「素人」らしい愚直な計算をして、なおかつ、それを間違え、そんなこんなでほぼ丸一日、「時間を潰す」ことが出来ましたから、「自慢」したいのでしょう(笑)。そもそも、こんな「時間の潰し方」を思いついたのは、「数式エディタ―MathType」、ダウンロード無料なのは、「30日間試用版」だけなので、ならば、30日たったら消・え・て・し・ま・う・(笑)、それまでに何か「有意義な」(笑)ことをしなくては、と、まさに、来年は生きていないかもしれない、が「口癖」の老人らしい、浅はかさなのでした。
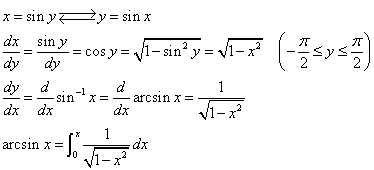
三角関数は周期関数ですから、同じyの値をとるxは無数に存在するが、定義域を区切れば、一つのxを指定することが出来るので、逆関数を考えることが出来る。その微分は、元の関数の微分dy/dxの逆数になることが知られている、証明どうやるんだったっけ?ともかく高校の教科書にも載っている。そこから、上のように、その導関数が、1/√(1-x2)という形になることがわかる。ならば、元のarcsinxは、それを積分すればよかろう。多項式として「級数展開」出来るのならば、多項式の積分は可能、かつ、簡便であるから、その積分もまた、多項式として表現できるだろう、という段取りだ。
で、私は、正直に(笑)、とりかかったのだよ、ずっと以前も、同じ過ちをした記憶がある、「オイラーの贈り物・人類の至宝eiπ=-1を学ぶ」吉田武(ちくま学芸文庫)、という非常に優れた書物を、引っ張り出して来て、思い出した。ちなみに、テイラー級数展開、というのは、次のような仕組みである。
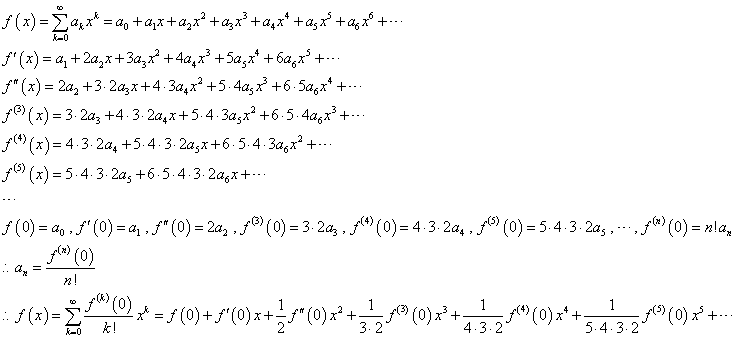
すべての関数が、無限項の多項式で表現できる、として(笑)、だったら有限項で終えたらそれは「近似値」にはなる、第n項の係数anは、上のように、n階微分係数と、階乗の記号を用いて表記できる。だから、これを得るには、繰り返し繰り返し、微分をしなければならないのであるが、周期性を持って単純な変化をしてくれるものならばよいが、そうでなければ、まことに、収拾がつかなくなる。その収拾がつかなくなって投げ出したものも、とってあるので、そのうち、訂正が出来たらここに並べてみたいとは、思う。そこで、この「オイラーの贈り物」に紹介されていた、数学の「プロ」なら、誰でも知っているべきことなんだろうが、もちろん、私は知らなかった(笑)、実に鮮やかな方法、これとは似て非なる関数、1/√(1+x)を、唐突に(笑)「思いつく」のである。なぜなら、こちらは、繰り返しの微分に優れて周期性があり、実に簡便に「展開」出来るからだ。そのうえで、多項式に展開できてしまったうえで、え、この関数って、このxのところに、-x2「代入」すればいいんでしょ?、と、しれっと(笑)、言うのである。やってみよう。
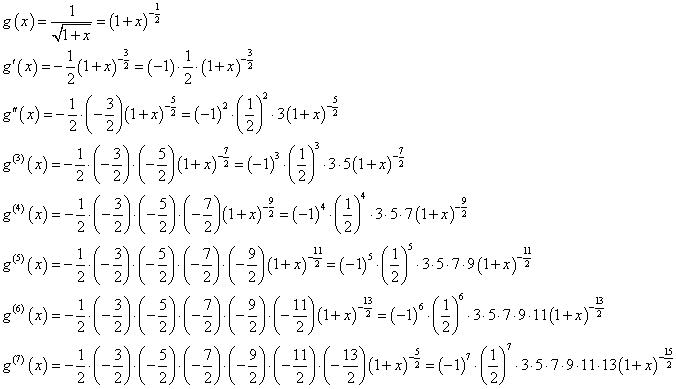
ここでも、奇数ばかりが順に並んだ掛け算を、階乗の記号を用いた分数で表現する手管を使う。
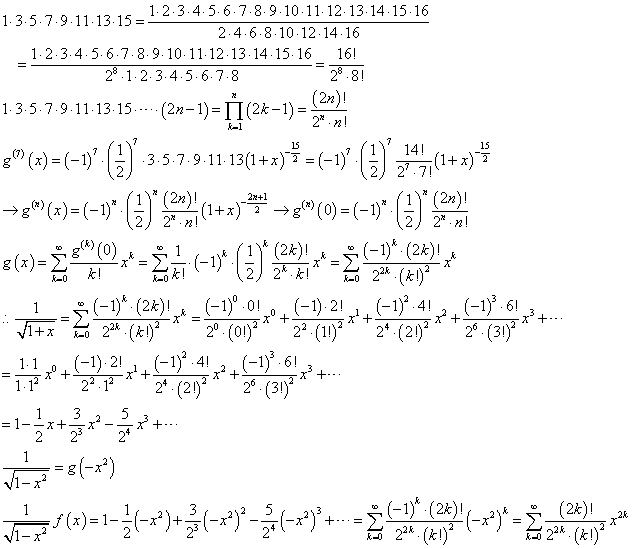
出来上がり、ですが、これは、まだ、arcsinxの導関数だから、これを、今度は、項別積分する必要がある。
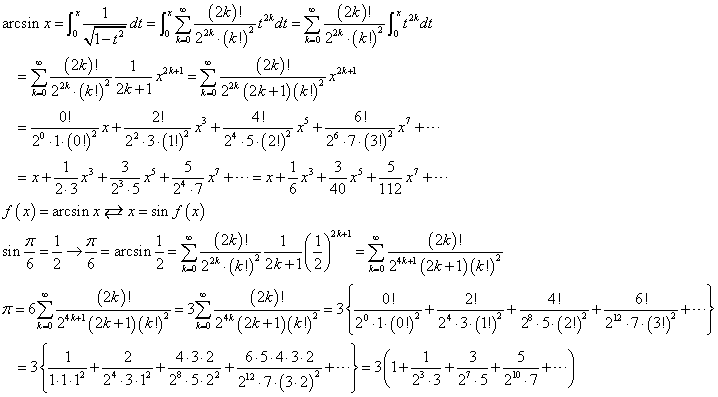
そして、最後に、上でも述べたように、sin(π/6)=1/2の関係を用いて、ほら、上の「算法少女」の式と、同じになった。
ついでに、元数学の「先生」ですから(笑)、得意そうにひけらかしますが、(2k)!/(k!)2の部分、「組み合わせcombination」、n個の異なるものから、k個取り出す方法の場合の数、nCkの定義からわかるように、これは、2n個の異なるものからn個取り出す方法の数を表しています。何か意味ありげ(笑)なのですが、意味ありげであることしかわからないので(笑)、本当はさして「得意そう」でもないのでした。
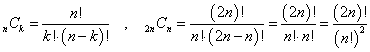
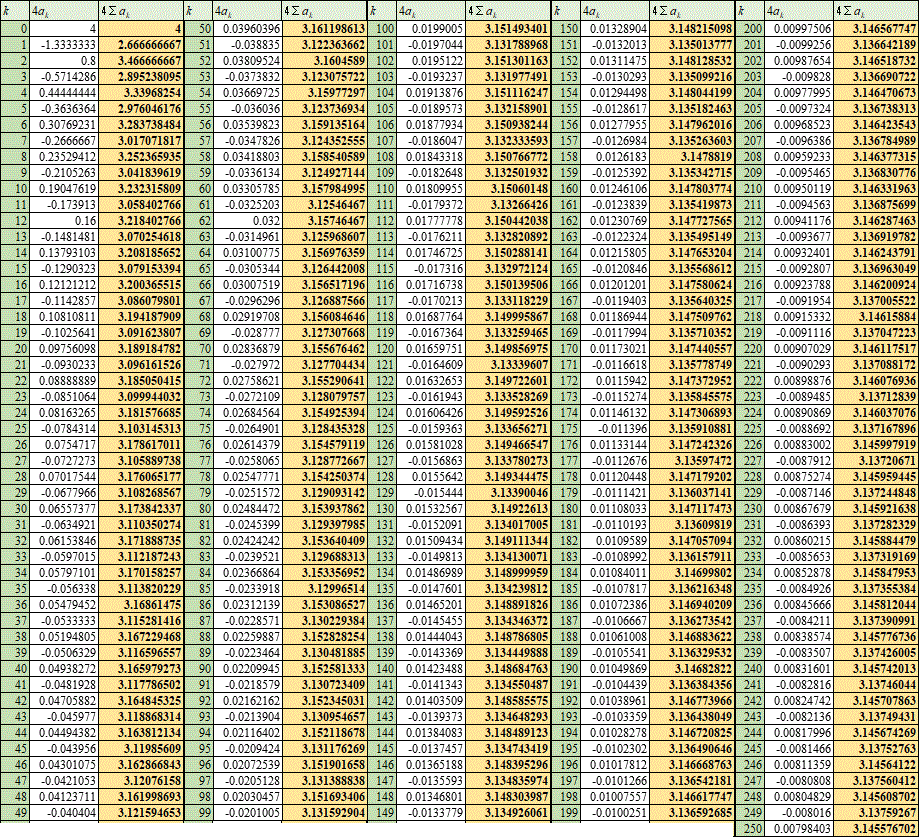
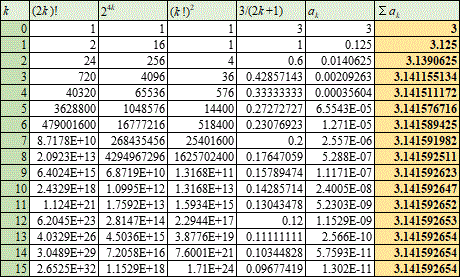
表計算ソフトで計算した結果を見てみましょう、なかなか収束が速いですね、もう8項目くらいから、3.141592、ぐらいまで合ってるじゃないですか。他に、逆正接関数arctanの級数展開を用いた、πの近似式もあって、ライプニッツの名が冠されていて、形がものすごくシンプルなので有名、私も知っていたくらい、だが、これは、収束が遅くて実用に適さない、と言われている、そういわれると、どのくらい「適さない」か知りたくなるのも人情なので、そのうち、そう、数式エディタ―の「30日試用期間」が切れないうちに(笑)、やってみる。
「出来なかったのが悔しかったので」などと言う「うつ病」患者らしからぬ感情の昂ぶりがあって(笑)、夜半までかかって、晴れ晴れと(笑)、完成。奇数項と偶数項で、共通因数にxを持つか否かが異なってくる、そんな「感じ」を、手にしてしまえば、計算間違いをしたときには、ああ、今まさに、計算間違いしていそうだな、ってわかる、森毅先生も、確かどこかでそんなことをおっしゃってました、数学というのは、特に、長い長い式を変形する、などという作業は、まことに「身体的」な作用なのであって、そう、それは、「労働に似ている」(笑)、のです。えっと、ゴダールの「パッション」に出てきた台詞です(笑)。
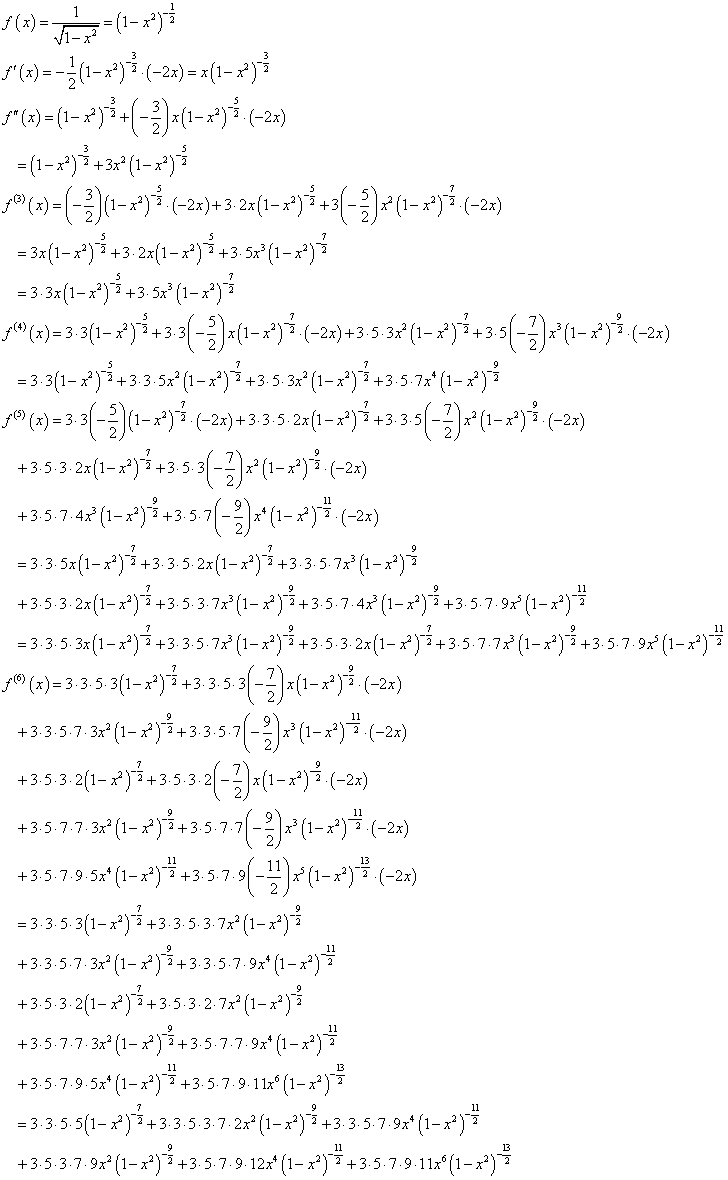
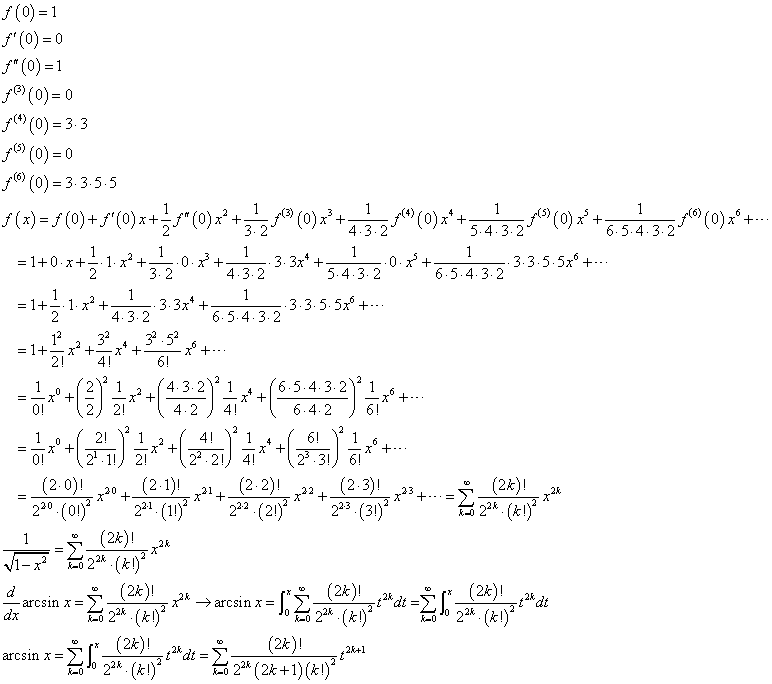
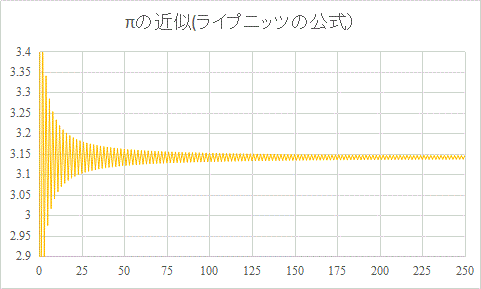
arctanxの級数展開から、πの近似値を求める話、今度も、「正直」に積分をしてはいけない(笑)のであって、また、巧妙な「すり替え」が行われます。一番下に得られたのが、一名「ライプニッツの公式」とも呼ばれるものです。どのくらい「収束が遅い」のかも、調べてみましょう。
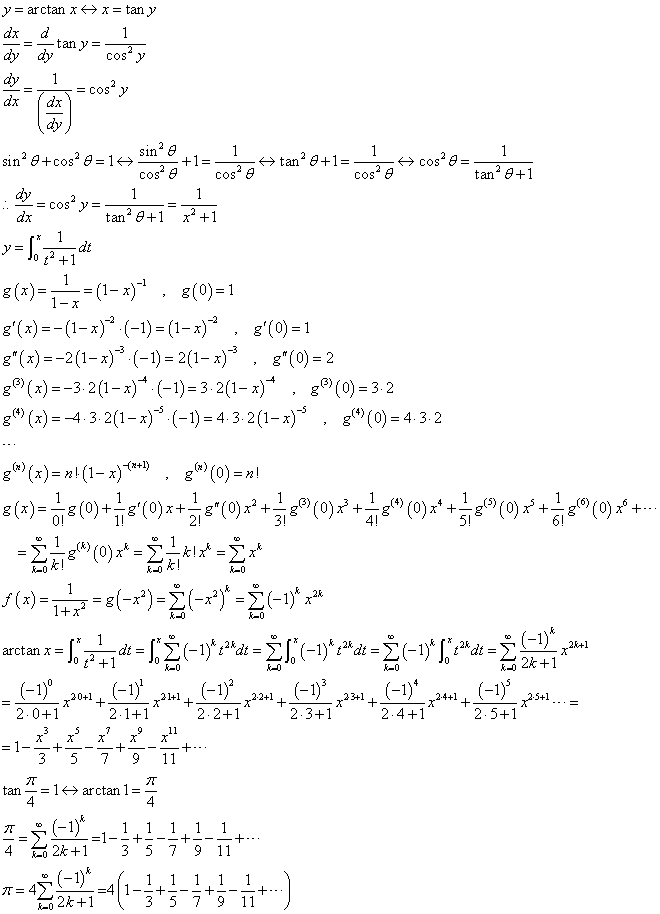
プラスとマイナスの項が交互に出てくるのだから、振動しながら近づくのであろうことは想像されます。それにしても、確かに、「遅い」ですね、100項目くらいから3.13と3.15のあいだを行き来して、その幅が、250項目くらいまで来ても、あまり縮まりません、確かに、これでは、「実用」にはならないでしょう、「円周率」に、どんな「実用」があるかは、さておき。