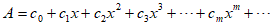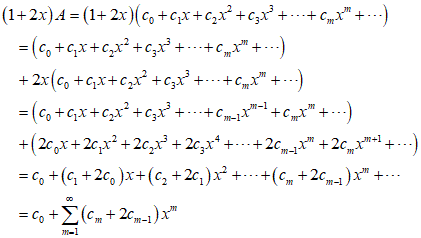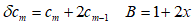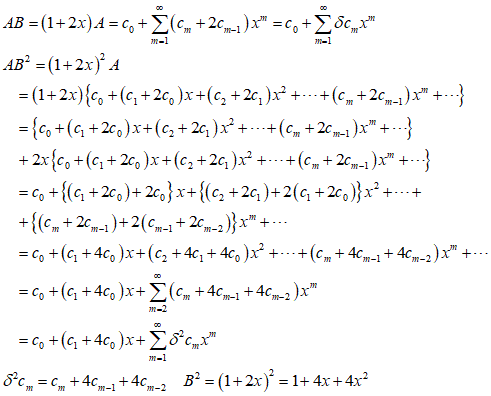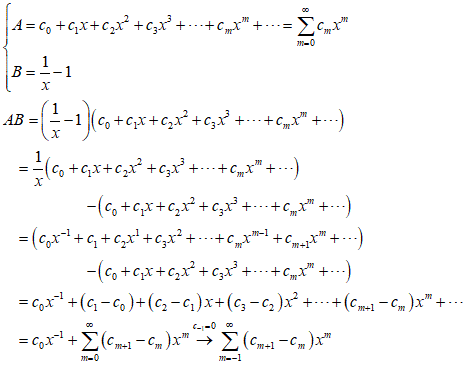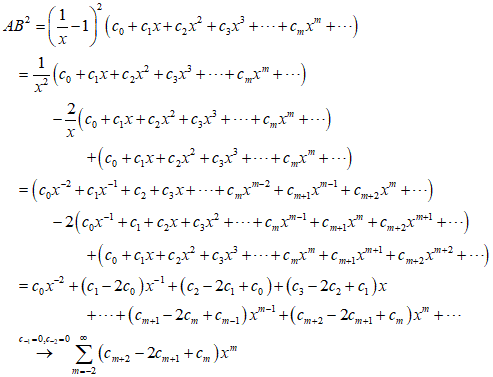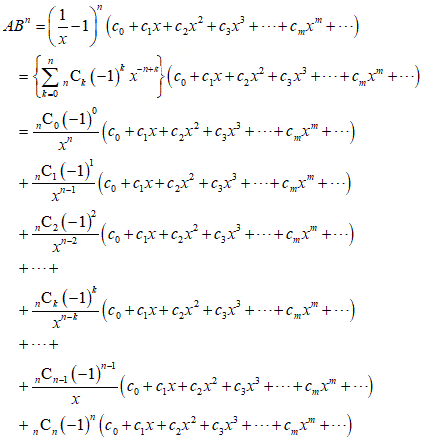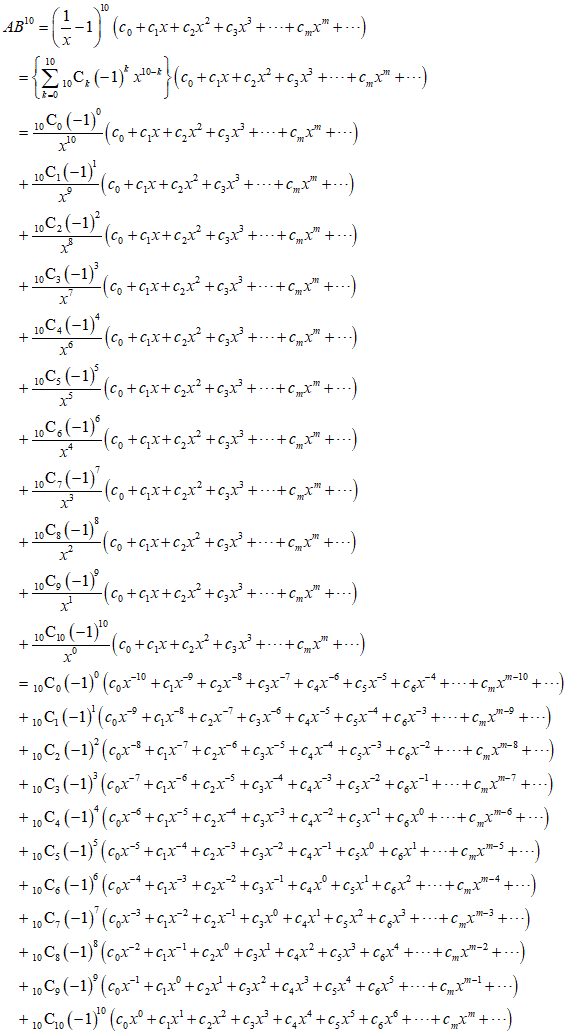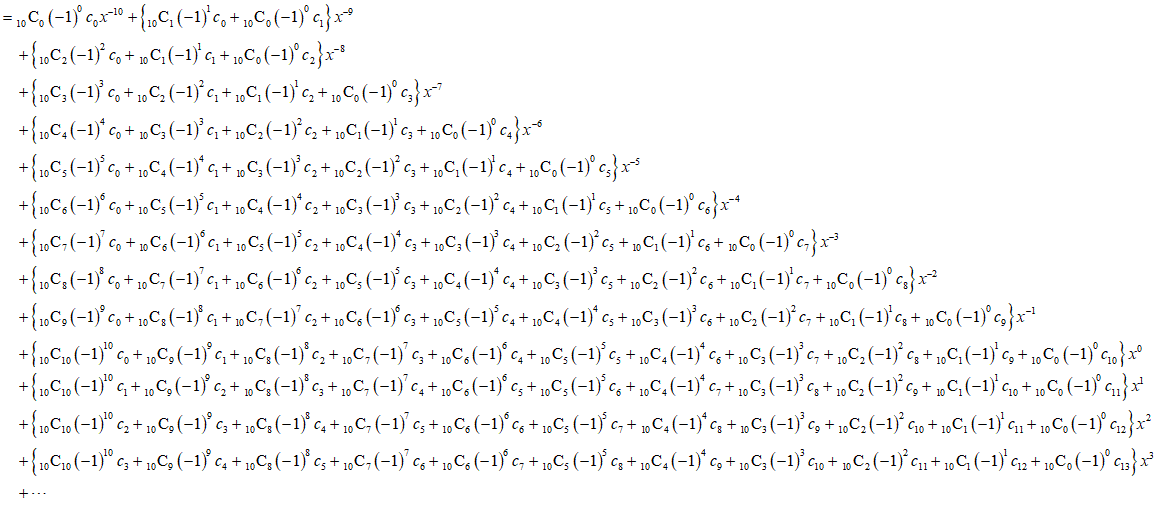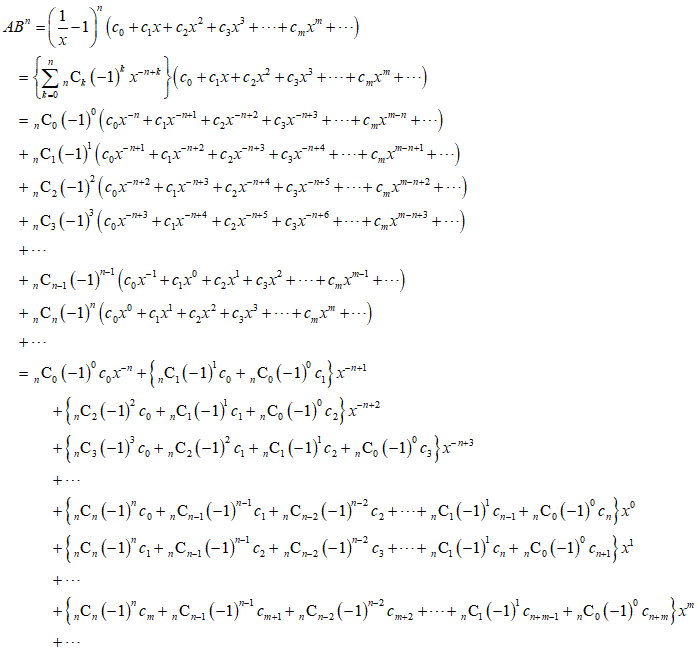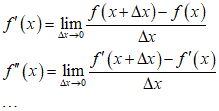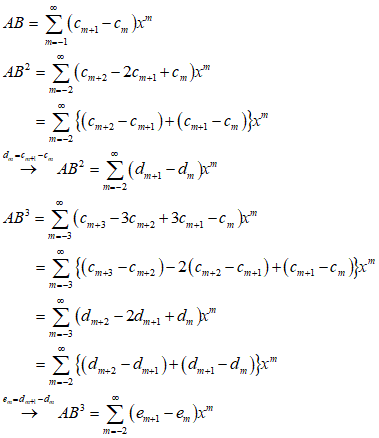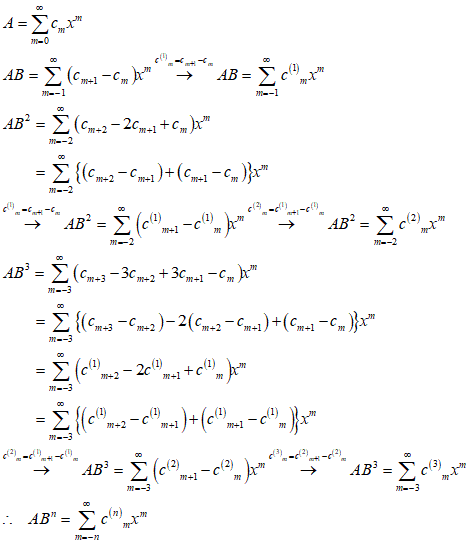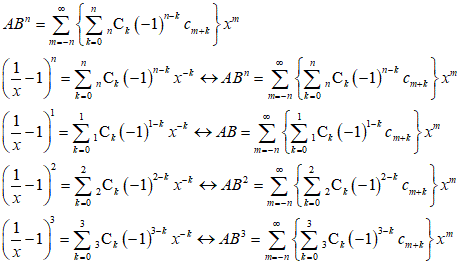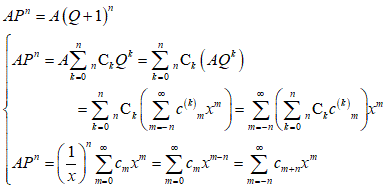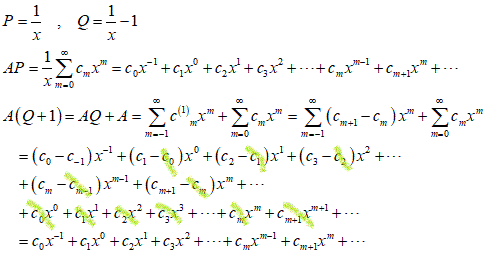ラプラス「確率の哲学的試論」（岩波文庫）、「母関数」に関する記述は、このままでは難解で意味不明、ということで、訳者の内井惣七氏が、詳細な注を付けてくださっているので、それに従って、・・・
そのために考え出された方法のなかで、わたしには最も一般的で最も単純だと思われるものは、母関数の考察に基づいている。その考えを以下に述べよう。
一つの変数xを持つ関数Aが、この変数の累乗の大きさを昇っていく順に並べられた級数に展開されているものとしよう。これらの累乗の任意の一つx^mにかかる係数は、指数すなわちこの累乗の回数を示す数mの関数となろう、そこで、この係数はc_mと表現できる。わたしはこのAをこの係数―すなわち指数mの関数―の母関数と呼ぶ。

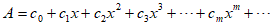
さて、級数に展開されたAを同じ変数xの一つの線形関数―例えば、1プラス変数の二倍1+2x―で乗じると、この積は新しい母関数となり、この変数の任意の累乗x^mにかかる係数は、Aの同じ累乗の係数に、一つ小さい累乗x^m-1の係数の二倍を加えたものに等しい。

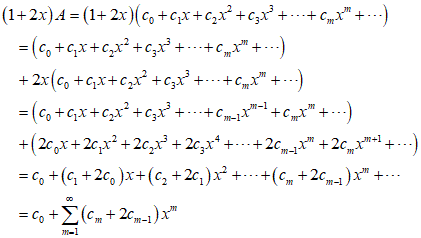
・・・積における指数のこの関数は、このようにAにおける指数の関数から派生したものと見なすことができる。この派生した関数は、もとの関数の前にある記号をつけることによって表現できる、例えば、その記号をδとすれば、各係数はδc_mとなる。この記号によって示される派生は乗じる関数に依存する。この乗じる関数をわれわれは一般にBで表わし、・・・

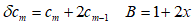
AとBの積にさらにBをかけると、これはAにBの2乗をかけることになる。これによって第三の母関数が形成され、これにおける変数の任意の累乗の係数は、最初の積において対応する係数と同様に派生的に得られる。したがって、先の派生した係数の前に同じ記号をつけることによってこれを表現することができる。このとき、この記号はAの級数の対応する係数の前に2度書かれることになるが、2度書く代わりにその記号を2乗する表現をとる、例えば、δ²c_m
同じやり方を続けて、AにBのn乗をかけると、・・・

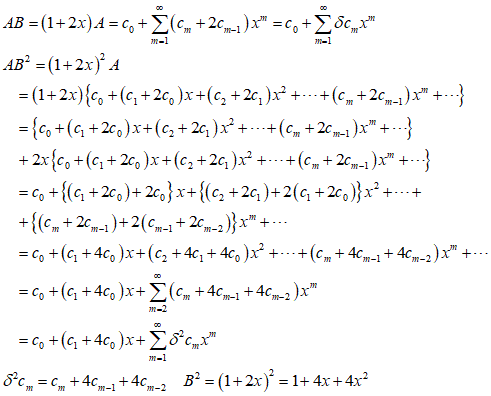
最初の1、2項が、別に処理しなければならないところが、次第に面倒になっていきそうだが、ならば、c_mの添え字mが負になったのはみんな0にする、なんて決めてしまえば、表記はすっきりするよな、そうしてみよう（笑）、

で、その上で、これを、「一般化」すると、・・・

凄いね（笑）、こんなこと、正直、一度も考えたことなかった、改めて、もう、済んだことだからいいけど（笑）、「私、数学の先生なんです」、なんて澄ました顔して歩いていたことに（笑）、猛烈に「赤面」すると同時に、いやはや、「近代合理主義」も「フランス革命」も、侮れないではないか（笑）？、と今頃になって、反省。
・・・、次に「差分」の概念が導入されるらしい、
関数Bは1を変数で割ったもの1/xだとしてみよう。そうすると、AとBの積において、この変数のある累乗x^mの係数はAにおける一つ大きい累乗x^m+1の係数となる。したがって、AにBのn乗をかけると、この係数はAにおいてnだけ高い累乗x^m+nの係数と等しくなる。

もしBが1を変数で割ったものマイナス1、(1/x)-1であれば、AとBの積では、この変数の係数は、Aにおいて1だけ大きい累乗の係数から同じ累乗の係数を引いたものとなる。したがって、これは関数Aの係数において指数を1動かしたときの有限差分となる。

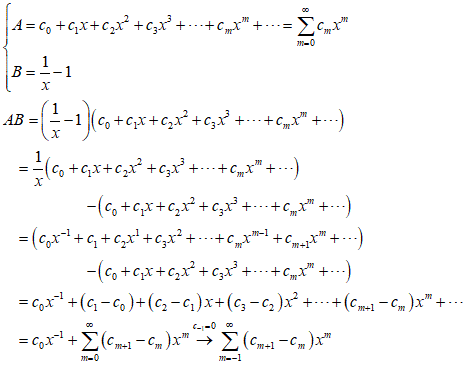
かくして、AにBのn乗をかけた積では、係数はAの対応する係数のn階の差分である。・・・
と言われましても（笑）、いきなりはわからないので（笑）、一つ一つ、やってみる、・・・、


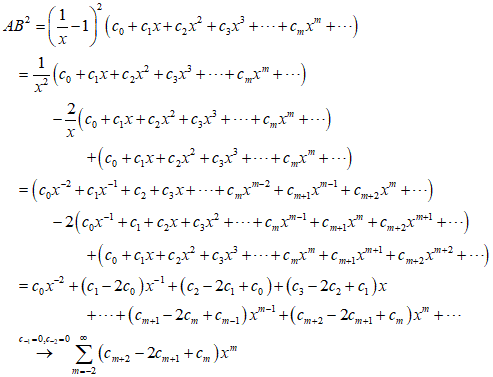
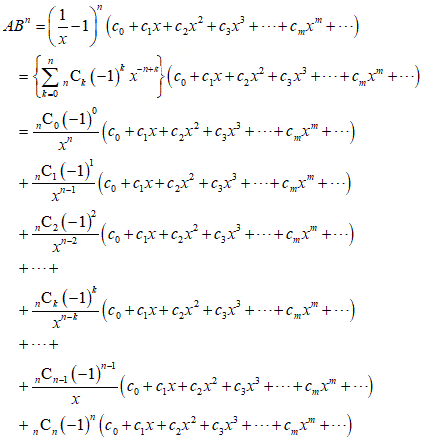
嗚呼、ややこしい、例えば、10乗の場合だったらば、x^-7の係数が、水色、、x^-2の係数が、ピンク、x⁵の係数が、黄色、こんな表を作って、参考にする、



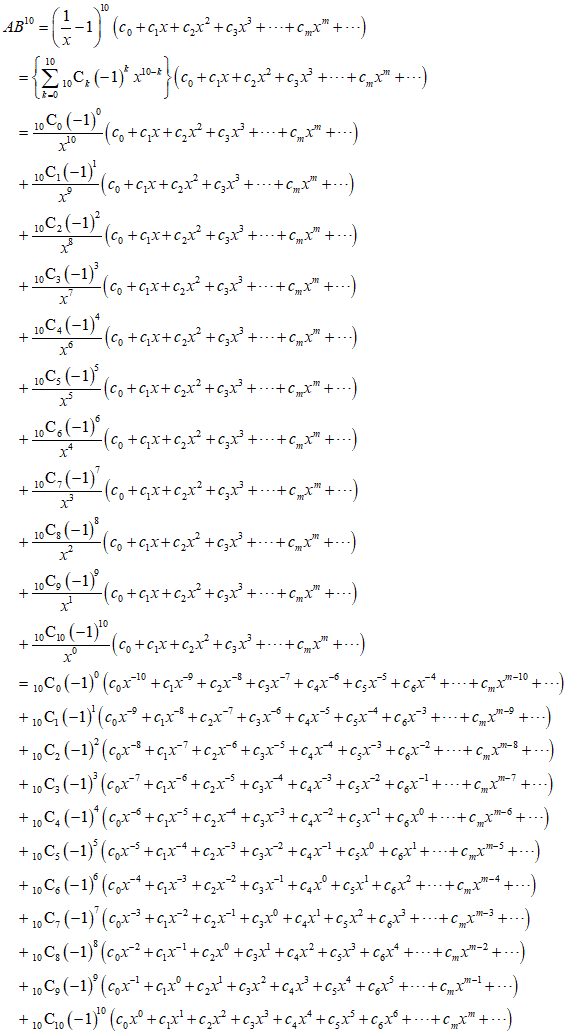
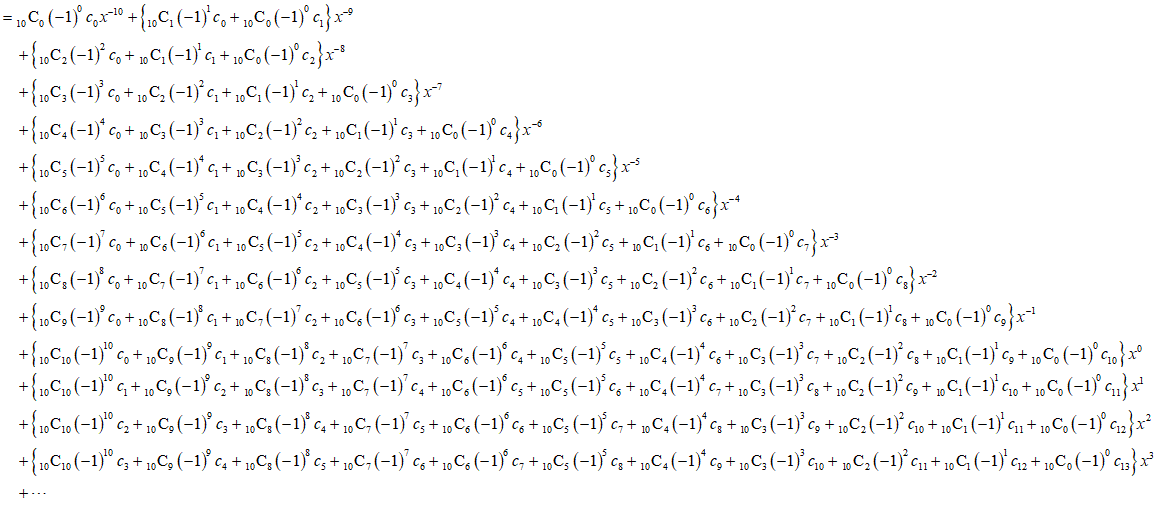
やっと飲み込めた気がする（笑）、では、n乗、

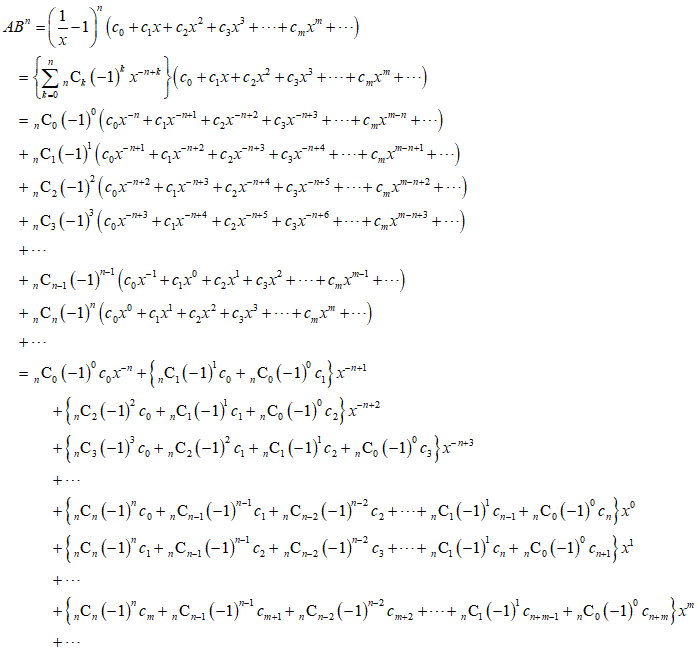
ここで、例によって、係数c_mの、添え字が負になるものはみな0とすれば、

これが、「n階の差分」である、というのが、どういう意味か、あんまり、というか、全然わからんが（笑）、今日のところは、ここまで。
「差分」、という言葉の意味について、考えてみましたよ。もとより「ばったもん」（笑）の数学教師だったのだから、仕方ないですが、あたし、それでも一応（笑）、大学院の入学試験に合格するくらいには、「高等数学」勉強したはずなんですが、あんまり聞き覚えのない言葉なんだな、高校数学で言う、数列の「漸化式」、a_nとa_n+1との関係式、を、元来は、「差分方程式」と呼ぶんだ、なるほど、稠密な連続変数の世界の「微分方程式」の「微分」dx、の、離散変数の世界での対応物が、「差分」a_n+1-a_nなんだ、ということは聞いたことがあるし（笑）、その昔、月間残業200時間超（笑）のプログラマ時代、自然界の拡散現象、などを記述する「微分方程式」を、コンピュータ上でシミュレートする際には、あくまでデジタルな、有限回の繰り返し計算に置き換えねばなりませんから、これを「差分化」して解いているのです、と言われ、その聞きかじりを、時には人さまに吹聴したり(笑)もしていたのですが、じゃあ、「階数」、微分の場合なら、x軸上の微笑変化に対する、関数値の変化を取り出す、という「手続き」を、屋根の上に屋根を重ねるように繰返す、謂いなのだから、

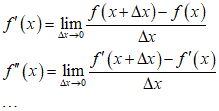
これが離散変数の世界なら、番号が一つ異なるものの差をとる、という手続きを、やはり、屋上屋根を重ねる如くに、繰り返せばよい、
b_n=a_n+1-a_n
と名付け、これが、高校数学の教科書風には、1階「階差数列」、ここでのいい方なら、1階「差分」、さらに、
c_n=b_n+1-b_n
を第2階の「階差数列」、2階「差分」、以下同様、・・・、そういう目で見ると、

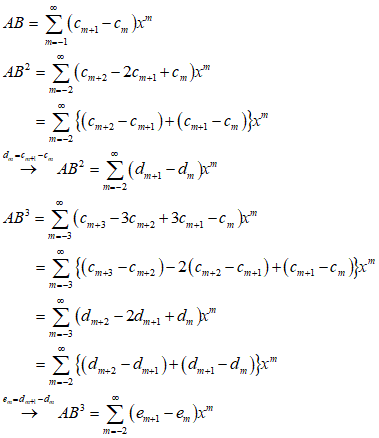
c_nの1階「差分」をd_n、2階「差分」をe_nとすれば、ABは、1階差分を係数とする多項式、AB²は、同じく2回差分を係数とする多項式、AB³は、3回差分を係数とする多項式、ならば、帰納的に類推して、ABⁿは、n階差分を係数とする多項式、ということになるであろう？記号の添え字が難しいな、ちょっと苦し紛れだが、高階微分の記号にならって、c_nのn階差分を、c⁽ⁿ⁾_n、とでもしてみるか、

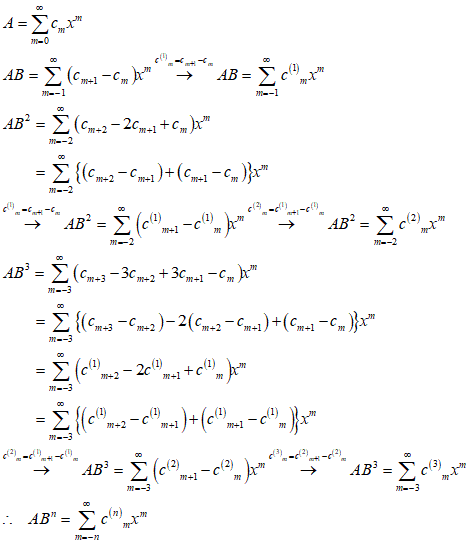
じゃあ、上の苦労した計算は、何だったのだ(笑)？いや、それはそれで、実りあったのである(笑)、いや、実りなんかなくてもよかろう？「苦労」が「水の泡」になったと嘆くのは、その「苦労」をもっとほかの「生産」に振り向けていれば、もっと「利得」が得られていたのに、ってことだろう(笑)？あんた、もう、そんな段階(笑)じゃないじゃん？もうじき死ぬんだろ？死ぬまでの残された時間すら使い道、思いつけなくて、こんなことして「潰してる」んだろ？だったら、「つぶれて」よかったね、と言いなさい。

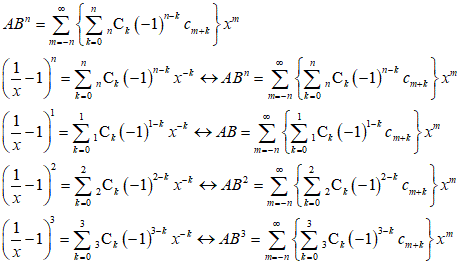
ね、こうして{(1/x)-1}ⁿの、「二項展開」式と並べてみれば、上でせ・っ・か・く・得られた式(笑)、ちゃんと、「意味ありげ」じゃないか？
ラプラス氏の叙述は、この後、こう進む、ちょっと文字は変えるが、P=1/x、Q=(1/x)-1、とすれば、P=Q+1、では、
APⁿ=A(Q+1)ⁿ
は、恒等的に成り立つ、右辺を二項展開して、係数比較すれば、ほら、面白いことがわかっただろ？、とおっしゃるようなのだが、確かに面白そうではあるが、残念ながら、貧しい想像力では、それほど「ピンッ！」とは来ない(笑)、やはり、2乗か3乗で、お手柔らかな例示をしてみないと、いいじゃないか、そうやっていくらでも、長引かせておきなさい(笑)。

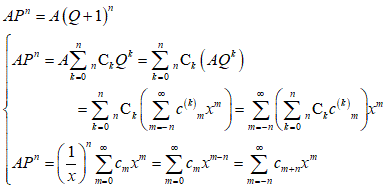
まず、1乗、

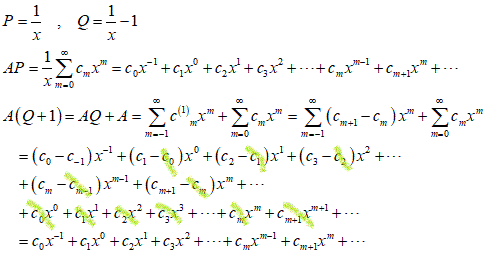
次、2乗、

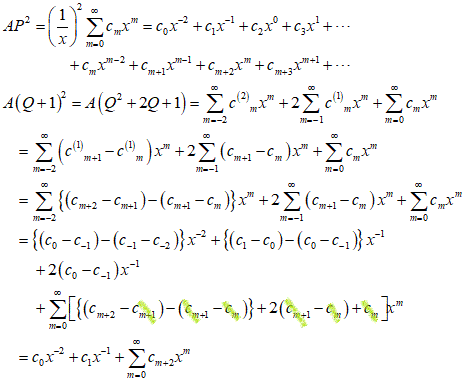
あの、そりゃ、「恒等式」なんだから、展開して各次数の係数比較すりゃ、同じになるのは当り前さ、当たり前のことも、やってみないとわからなかったんだから、まぁ、仕方ないじゃないか(笑)、という訳で、オチもないままに、何をしているかもよくわからないままに、しかし、「時間を潰せた」(笑)充実感だけはあったりして、とりあえず、終了。