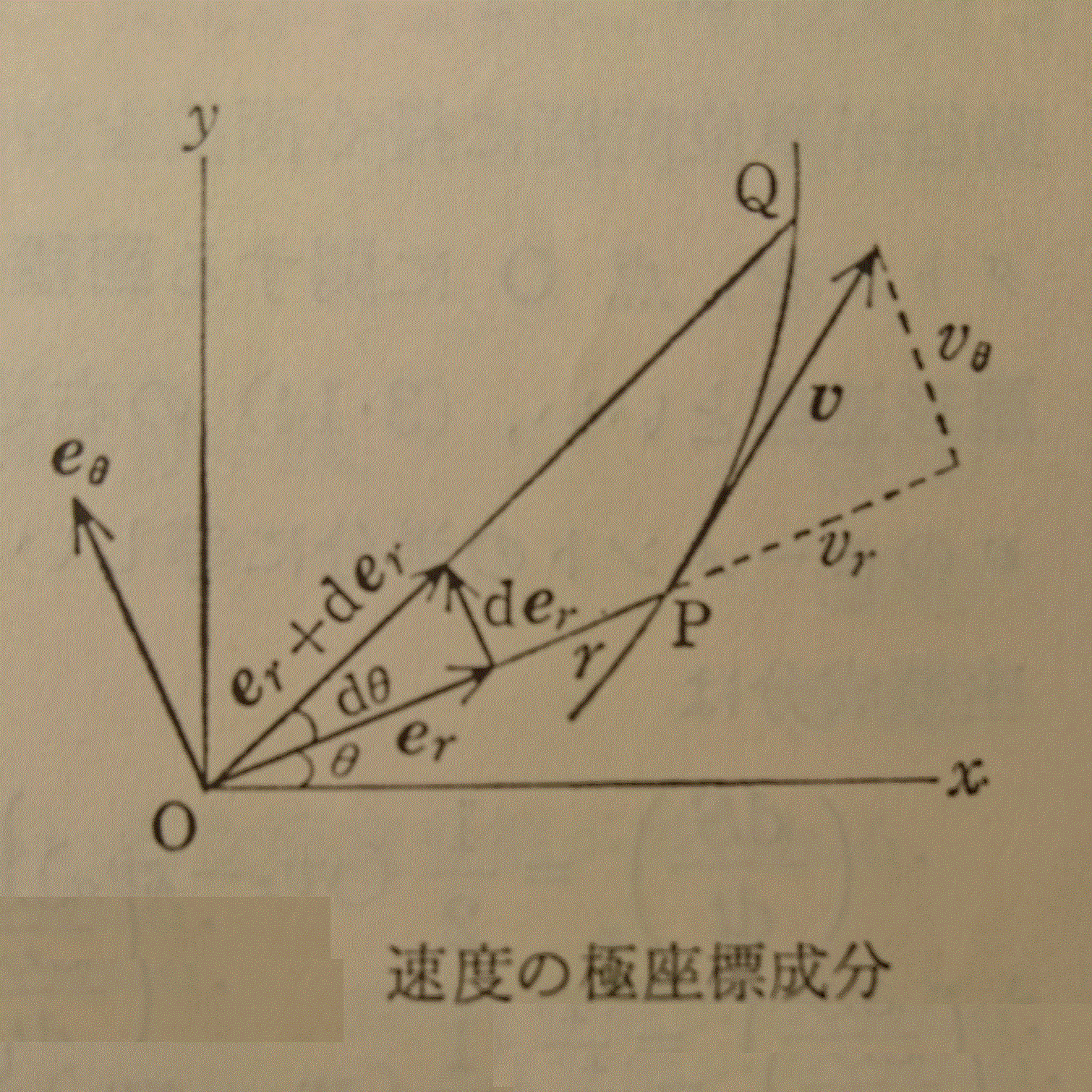
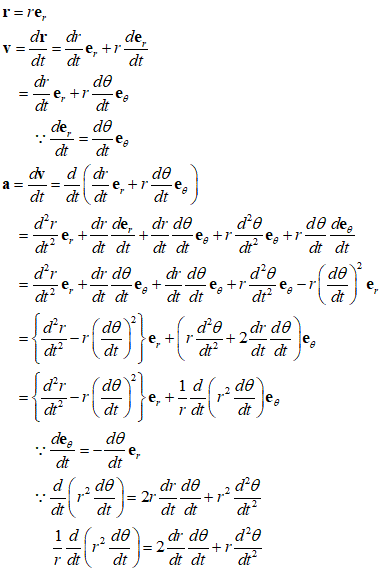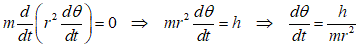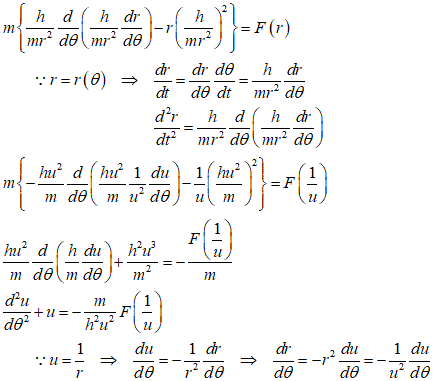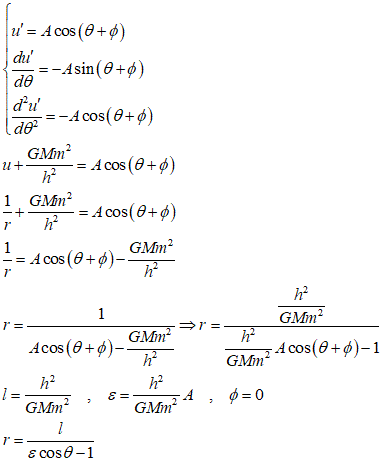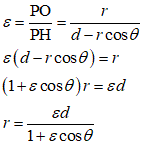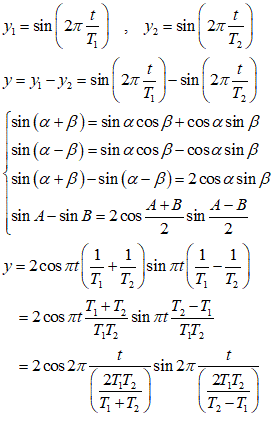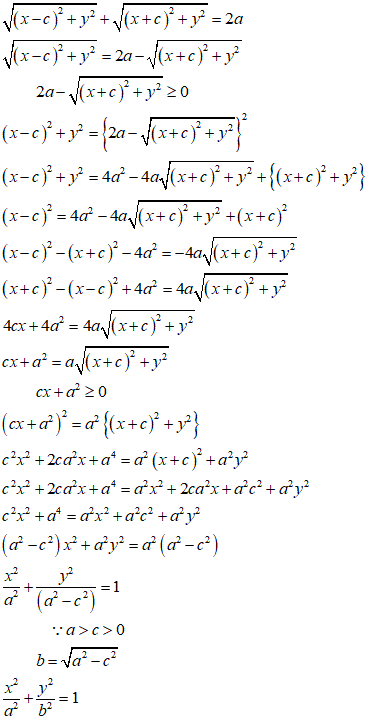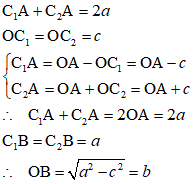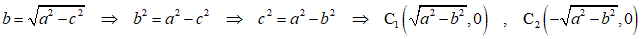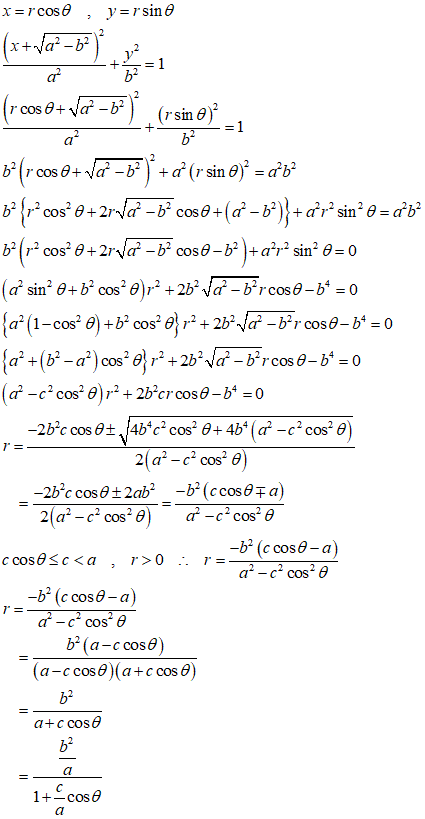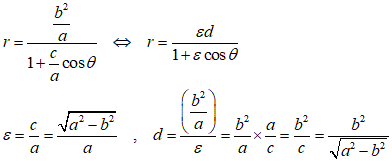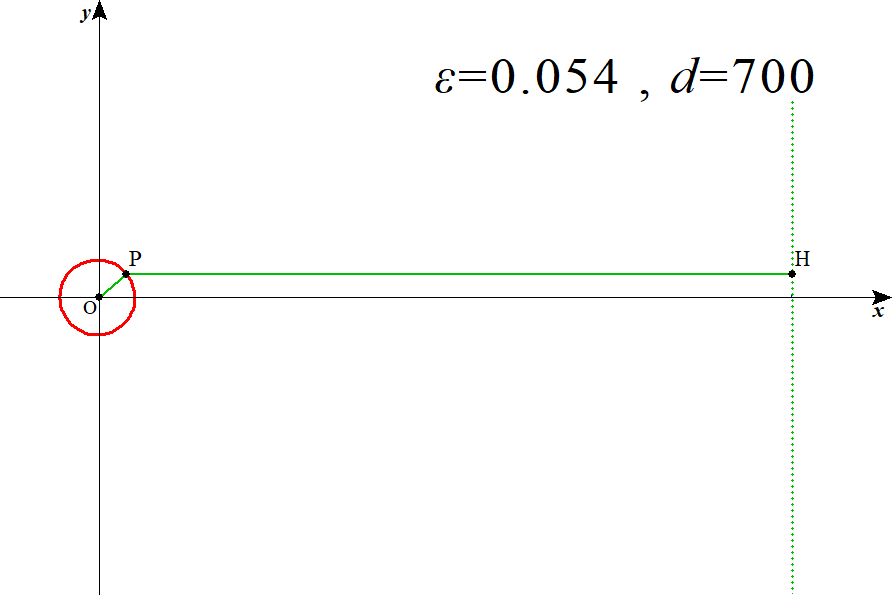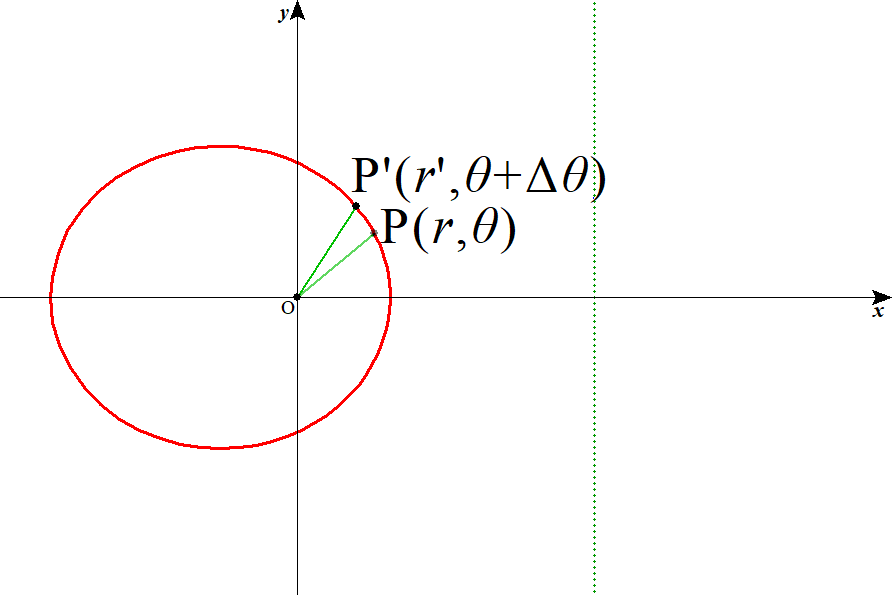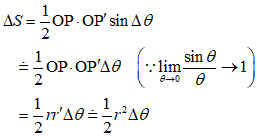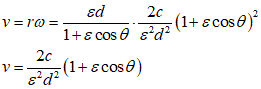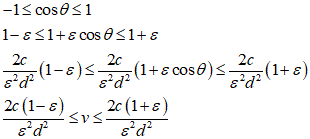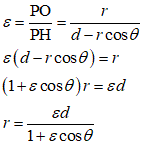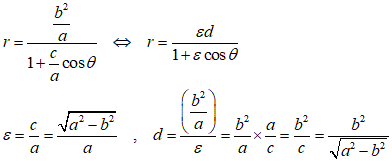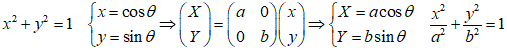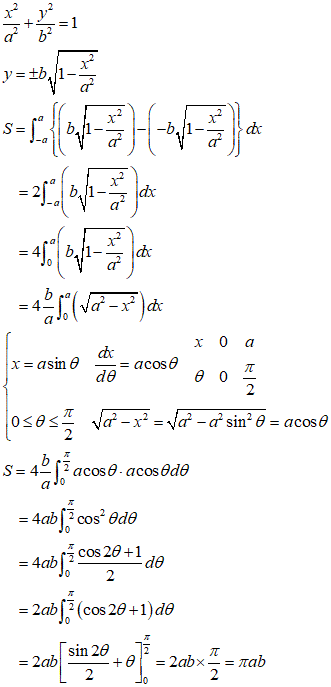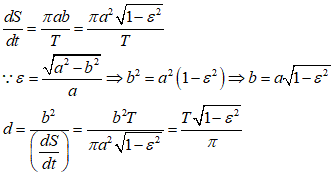極座標における、位置r、速度v、加速度a、を導く
ここに、er、eθ、はそれぞれ、動径、偏角成分の単位ベクトル
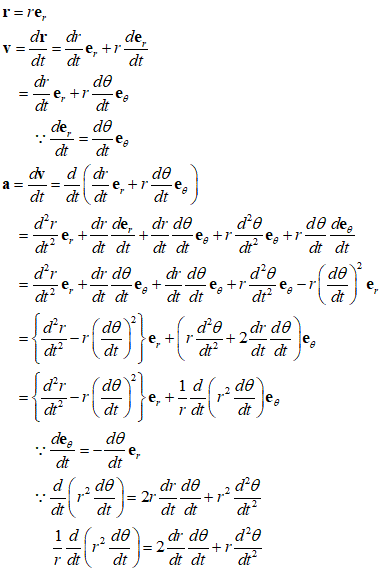

中心力場における運動方程式

θ成分の式の両辺にrをかけてから積分すると、
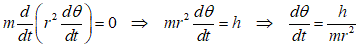
この↑真ん中の式は、「角運動量保存則」を表すことになるらしい、hが、その「角運動量」を表す定数
r成分の式にこれを代入、u=1/rなる変数変換を施す
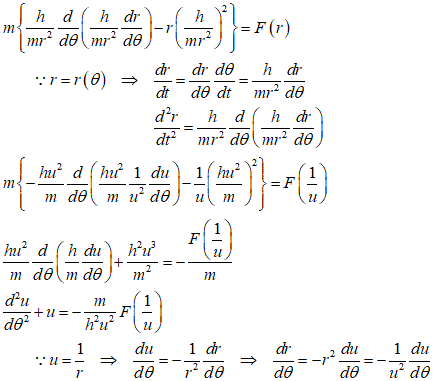
F(r)が「逆二乗法則」に従う力、すなわち「万有引力」とすると、Gは万有引力定数、M、m、は、いわば「対象」と「主体」となる2物体の質量、太陽―地球系で、地球を中心に考えるなら、Mが太陽、mが地球の質量を表すことになり、地球―月系で、月中心なら、Mが地球、mが月、ということになる
以下のようにθの関数uについての、線形2階常微分方程式となる、
変数変換を行って、

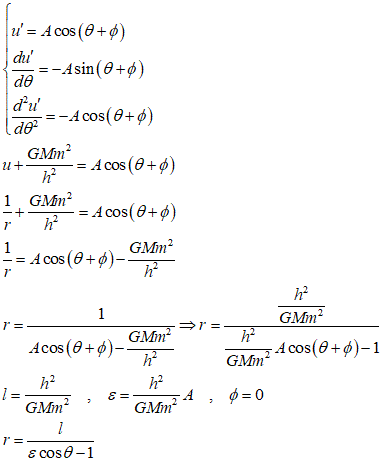
極座標による2次曲線(円錐曲線)の表示
動点Pから、極O(0,0)への距離と、準線x=dに降ろした垂線の足Hとの距離の比を、離心率εと定義すると、
ε>1、ε=1、ε<1、は、それぞれ、双曲線、放物線、楕円、を表す
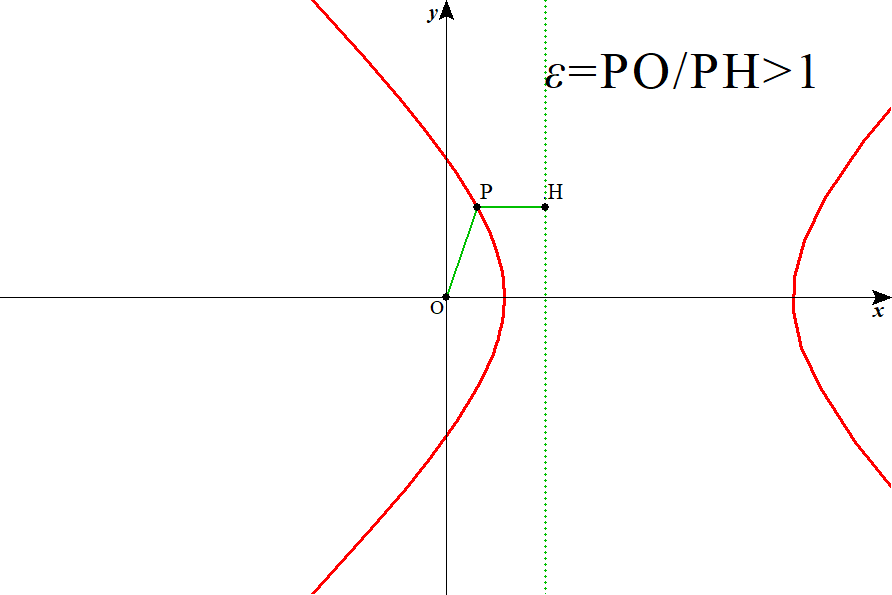

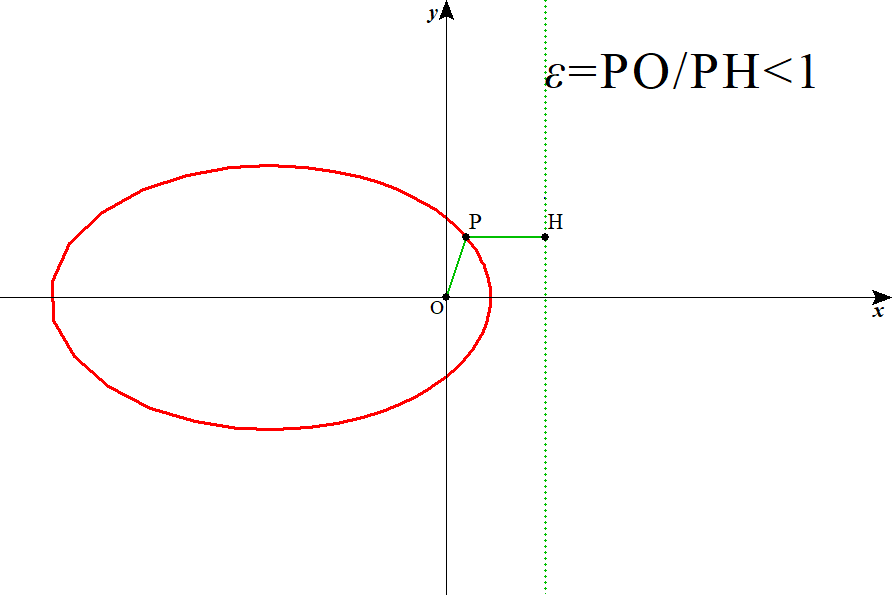
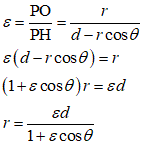
どうも、上の微分方程式から導いたものと、符号が一か所、合わないんだが(笑)、上の方は、分子のlは、角運動量h、万有引力定数G、2天体の質量M、mなどで出来ており、しかも2乗まで付いてる、疑いもなく正の値、分母の符号は、積分定数φの取り方如何で、何とでもなりそうだが、そうともいかない、グラフソフトに問い合わせてみると(笑)、どちらでも同じ絵を描いてくれるみたいだし、その、辻褄は、また後日、ということにして。
なんでこんな話が始まったか?先日の満月が、「スーパームーン」だと聞いたからだ。
月の地球に対する公転軌道は、かなり円に近いものの、万有引力を中心力とする運動方程式から導かれるように(笑)、地球を一方の「焦点」とする楕円軌道なのであって、となると、それら2天体間の距離は、周期的に増減を繰り返す、その最小と最大をもたらす地点を、「近地点・遠地点」、これは地球―月系だからこういう言い方なので、「近い」「地点」ではなく(笑)、「地球」に「近い」「点」なのだ、太陽―地球系では、「近日点・遠日点」という、その「近地点」と、「満月」が重なれば、一番近くて大きく見える満月、すなわち「スーパームーン」となる、ということであるらしい。
その楕円軌道の周期は、月の地球に対する公転周期、T1=27.32166181、単位は「日」、他方、月に満ちかけの周期は、平均朔望月、T2=29.53055556、約二日の誤差は、月が地球の周りを一周する間に、地球も太陽の周りを、移動するから、地球から月を見たときの明るい部分の大きさが同じになるには、やや多めに回らなければならない、からで、これは中学校の理科の教科書にさえ、書いてある、中学生としての記憶にあるのではなくて、ずっと後に大人になって、中学生に向かって、まるで昔から知っていたみたいな顔をして「教えた」ときに、初めて知ったのである(笑)。
ならば、これら二つの周期の異なる振動が、重なり合ったらどうなるか?を調べればよかろう、と素人は考えた、楕円の一方の焦点との距離が、正弦関数的に振動するわけではないから、もちろん、怪しいところは、ある、下のごとき美しいグラフを得て、あるとき、「満月」と「近地点」が重なったとすると、次は、この包絡線の表す振動の半周期、後にまた同じことが起こるであろう、つまり、「スーパームーン」の周期が得られるであろう、と考えたのだが、果たしてそれを計算してみると、365.2615033日、平均太陽年365.242日に極めて近い値が出て、何かすごい発見をしたかのように、躍り上がりかかったのだが(笑)、いや、少し待て、
うまくいきすぎる、ということには、「ウラがある」(笑)、と疑うべきだ、話が循環しているかも知れない、もともと、月の公転周期と、平均朔望月の差の中に、地球の太陽に対する公転周期に関する「情報」が含まれていた筈だからね、
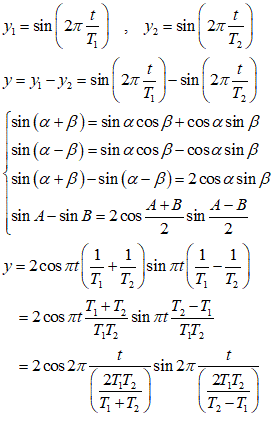

ちょうど一年経てば、「元に戻る」ことは疑いなかろう、それが「スーパームーン」の周期、と思ってしまったのだが、何か、考え違いだったかもしれない、いや、考え違いだったのだろう、某ペディアの記事は、なかなか不親切で要領を得ず(笑)、しかし、「スーパームーン」の周期が411.8日である、とだけは、断言されている、
はっきり覚えている「スーパームーン」、というか、その時はじめてこの言葉を聞いたのだが、あれは、2016年11月頃、ちょうど、「高江」の工事の頃、朝の五時頃とかから出かけて、N1ゲート前で座り込みをして、いっぱい空しい思いをして、疲れて、帰りに、読谷村の、道路脇から、確かに極端にでかく見えたその満月の写真を撮ったのと覚えている、調べてみると、それは、2016年11月14日、そして、今回のが、2020年5月7日、それぞれを、エクセル互換表計算ソフトの「日付シリアル値」に直すと、42688、43958、その差1270、なるほど、その411.8日なる周期で除してみると、3.08、なかなか整数に近い良い値を示している、というわけで、相変わらず、またしても「オチ」のない話だが、せっかく、半日以上、潰した作業なので(笑)、「成果」は、残しておくことにする。

今宵が満月であることは、もちろん把握していたが、大層珍しい「スーパームーン」とやらであることは、他人様に教えてもらわないと、知りようがなかったな。11/14(月)高江 からの帰路、読谷あたり。
もう一つ、潮汐表に記された、月の出月の入時刻から、「月の出ている時間」をプロットしてみたところ、これまた「閑人」らしい「発見」であるが、約27.5日周期で、変動していることは、前にお話しした、あるいは、これは、月の公転周期だったのだ、と考えれば、辻褄が合うようにも、いや、しかし、どうして辻褄が合うのかは、よくわからないような(笑)、感じがしたので、これまた、備忘として記しておく。
x-y座標系で、別の定義から、楕円の式を導く、x軸上に、原典を中心にして左右対称に、C1(c,0)、C2(-c,0)、をとる、この2点からの距離の和、が一定値、2a、であるような動点P(x,y)の軌跡を求めたい、
PC1+PC2=2a
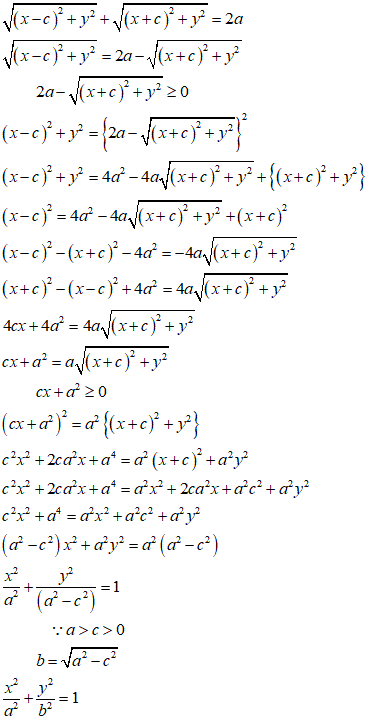
ここに、a、は「長半径」、b、は「短半径」、を表すことになる、なぜなら、
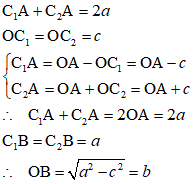
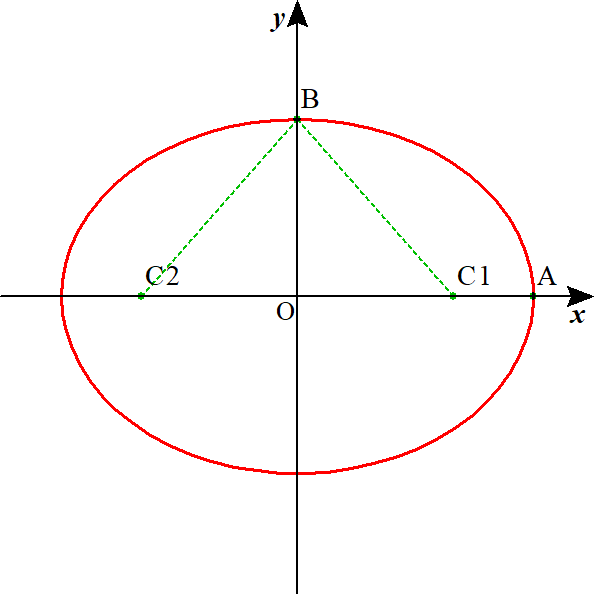
逆に焦点を、a、b、で表すと、
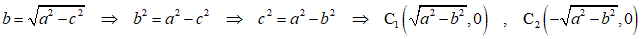
これと、上で得られた極座標表示のものとの対応をつけたいので、まず、C1が原点に重なるように平行移動すると、

x=rcosθ、y=rsinθ、を用いて、極座標に変換する、
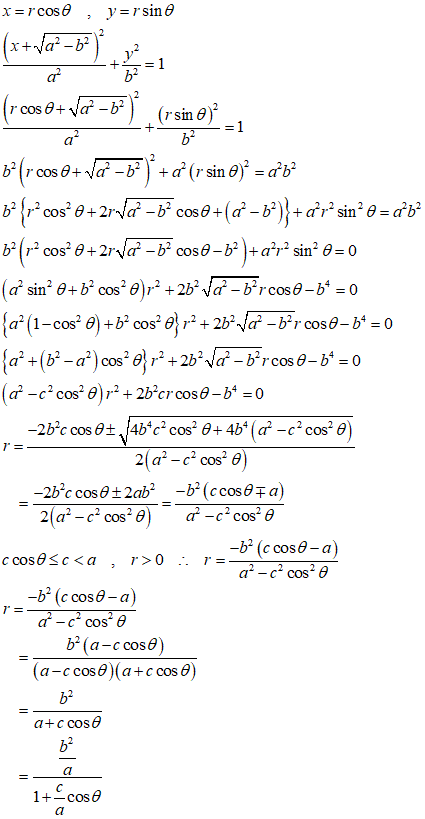
おや、うまくいくまいと、半ばあきらめてたのに、うまくいったよ(笑)、
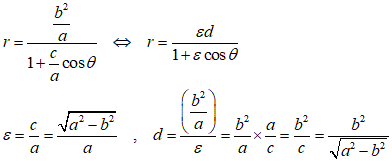
さて、ここで、某ペディアの「月」のページを開いてみると、
平均公転半径384400km
近地点距離363304km
遠地点距離405495km
離心率0.0548799
公転周期27日7時間43.193分
平均軌道速度1.022km/s
軌道傾斜角5.1454度
おそらく、「近地点距離」は、C1A=a-c、「遠地点距離」は、C2A=a+c、と読めるから、
これを材料にして、長半径a、焦点のx座標c、短半径b、長半径と短半径の平均、そして、上に掲げた式から、離心率ε、と、準線の位置d、を算出してみた、ご覧の通り、辻褄は合っている(笑)、これほど離心率が小さいと、普通の図面では(笑)、原点にほとんど重なる小さな小さな円になる、準線までの距離が、軌道半径の20倍近くあるので、縮尺を思いきり大きく、というべきなのかな、小さくというべきなのかな(笑)、とって描いてみたのがその下の図面、

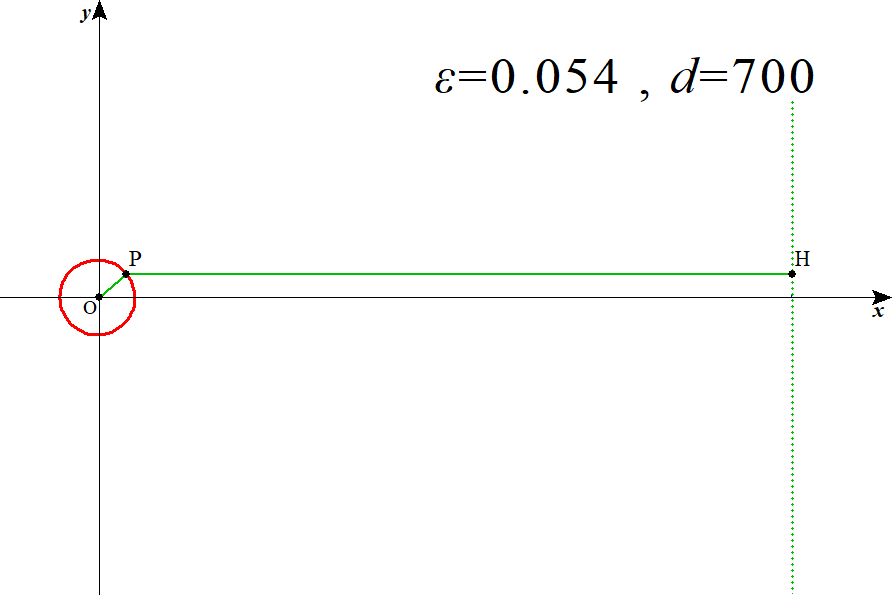
距離Lの彼方に、半径Hの円盤が浮かんでいるとしよう、人がこれを見る視角をαとすれば、
H=Ltanα
微小な角度については、tanα≒α、の近似がなりたつから、
H=Ltanα≒Lα
つまり、月の「客観的」な半径Hが不変であるなら、距離Lと視角αは反比例する、
「近地点」にいる最・も・大・き・く・見える満月、すなわち「スーパームーン」の、「遠地点」にある最・も・小・さ・く・見える満月、の半径の比は、「近地点距離」と「遠地点距離」の逆比、ということになろう、それが上の表に加えておいた、1.12という値、某ペディアの記事には、その値も乗っていたかも知れないが、もう、だいたい、興味も尽きてしまったので(笑)、もう、調べない、まずまず、そんなところなんだろう。
ところで、困ったことがひとつ(笑)、上に列挙した諸元の中に「軌道傾斜角」があるだろう、今まで、仰角の計算と称した図表を掲げたが、それ、全部(笑)、太陽と同じ、23.4度ぐらいだろ?と適当にやってたので、こんな小さいとは知らなかった(笑)、今までの表は、全部「没」になるんだが、もう、めんどくさいし、「老い先も短い」ってことで(笑)、直したりはしないことにする。
ケプラーの3法則
- 楕円軌道
- 面積速度一定
- 周期の2乗は、長半径の3乗に比例
円もまた、長半径と短半径が等しい、という特別な場合の楕円なわけだが、このとき、iiの、「面積速度一定」は、等速円運動、すなわち、角速度一定、に単純化される、実際の太陽―地球系も、地球―月系も、ほとんど、円に近似できるくらいの、つまり、離心率εが0に近く、したがって、準線への距離dがとても大きい、楕円であるから、そのように処理しても、そんなに不都合はないのだろう、高校の物理の教科書では、等速円運動への近似で論じてあるし、もとより(笑)「先生」たる私も、それしか知らなかったから、そうしてきた。
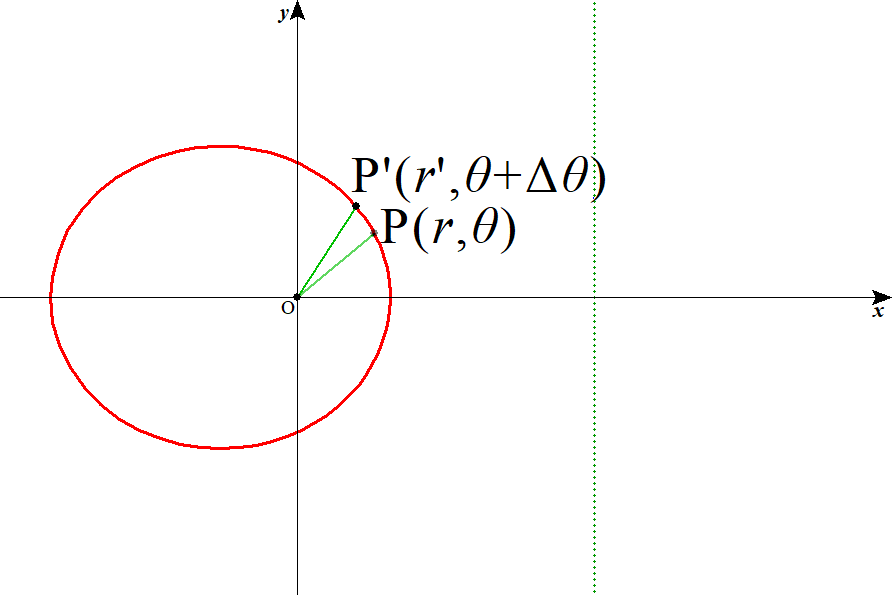
上図で、径OP、およびOP'、と楕円の弧PP'で囲まれる図形の面積は、Δθが十分小さければ、△OPP'で近似でき、その面積ΔSは、以下のように表せるだろう
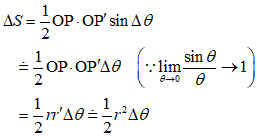
ならば、x軸、極座標では、「始線」と呼ぶのだったかな、偏角θの動径までの間に、囲まれる楕円の面積は、

と、計算できることになるが、この積分の方法を思いつかないのは、私が無能であるからなのか(笑)、あるいは、元来この積分が解析的に計算可能でないのか、そんなことも知らないほど(笑)、やはり無能であるか、どちらかなんだが、いずれにしても、一頓挫、だが、挫けず(笑)、「面積速度」とは、この、面積の、時間に対する変化率、dS/dt、の謂いであろう?それが、「一定」だというのなら、その一定値をば、cとでもおいて、それを用いて、角速度ω=dθ/dt、が、導かれるではないか?ただし、これは、dθ/dtが、他ならぬ、θの関数として得られたに過ぎず、これをtの関数にするには、私見では(笑)、以下のように、変数分離形の微分方程式を解かなければならないことになり、おや、それは、同じ形の、無理難題であることがわかり(笑)、元の木阿弥なのであった。「元の木阿弥」は、筒井順慶の「影武者」として、姿かたちのよく似た僧「木阿弥」が採用されていたが、捕縛されて発覚、元の、木阿弥に、戻ってしまった、という所以であったかと思う(笑)、筒井順慶は、本能寺の変の後、明智光秀側につくか、豊臣秀吉側につくか、決めかね、洞ヶ峠、これは、国道一号線の京都府大坂府の境あたりに、そんな名前の展望台があったからよく覚えている、で、「日和見」をしたことから、「日和見主義者oppotunist」の代表例みたいに扱われることになったのだ。

速度vは、角速度ωに動径rを乗ずることで得られるはずであろう、ならば、これは、以下のように、cosθのグラフを、上に平行移動しただけの、比較的簡単な形になるであろう、
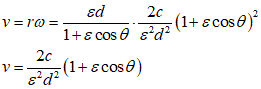
もとより、定数cなるものの値はよくわからないので、縦軸の目盛りがなにを表すかも不明であるが、
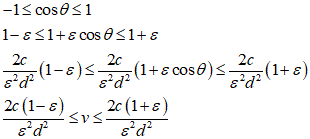
であるから、離心率εが1に比べて十分小さく、円軌道に近づけば、速度vもまた、一定値に近づくであろう、という、当たり前のこと(笑)、もわかった、
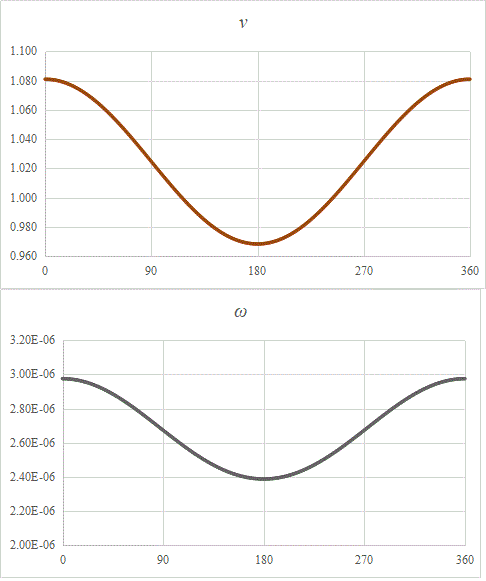
グラフ横軸はθを度数法で表したもの、ならば、θ=0、が「近地点」、θ=π、が「遠地点」、「面積速度一定」の下では、動径が短ければ、速度ないし角速度が大きく、動径が長ければ、小さくならねばならない、「近地点」では、速度、角速度ともに最大、「遠地点」では、逆に最小、という、別にこんな手間を掛けなくても(笑)、わかりきったことが、わかった段階で、ない「オチ」をつけて、中断、新しく引き入れた、子猫が、「かまってくれ!」と、とんでもなく喧しいし(笑)、・・・。
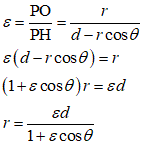
楕円の極座標形式の表式を導き、
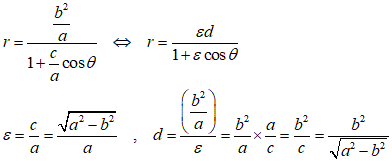
x-y座標形式のものとの比較から、これが得られたのであるが、よく考えて見ると(笑)、「準線」など、どこにあるのかよくわからないもの(笑)を考慮せずとも、「長さ」の次元を持ったものとして、たとえば「長半径」aのみ、あとは、「離心率」εを指定すれば、楕円の形状が確定するのであるな。

上で「面積速度一定」の法則から、その定数値をcなどと名付けてしまったが、これは、もっと上で、焦点のx座標として選んだものと混同してしまうから、気分がよくない(笑)ので、さっさと廃止しよう、楕円の面積を、極座標形式の成分によって得るのは、どうも無理であるらしいことが、「力学」の教科書の書きぶりから読み取れる、だが、楕円全体の面積は、もちろん、知られているのである。
半径1の円の面積は、π、楕円は、これを、x軸方向にa倍、y軸方向にb倍、不等拡大した図形、といえるから、面積は、これらの積をかけて、πab、
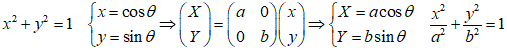
せっかくだから、閑だし(笑)、x-y座標形式での積分計算をお目に賭けよう、高校の数学III、でおなじみの論点である。
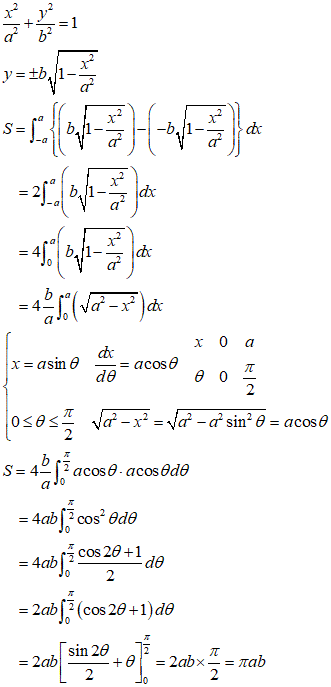
すると、楕円軌道の周期を、Tとすれば、その、一定なる面積速度を示す定数cは、これを用いて、表せることになる、すなわち
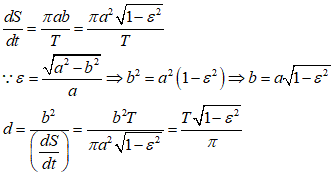
準線への距離dも、これで従属変数となる
こうして、たとえば、地球の周りをまわる月、というような楕円軌道についての諸元が、離心率ε、長半径a、周期T、の3つの数値データで、くまなく表せることがわかったのである、このうち、εは「無次元数」、aは「長さ」[km]、Tは「時間」[s]の次元を持つ
これらを用いて、上の速度vと角速度ωのグラフ、さっきは(笑)、縦軸の目盛りの意味、全然分からなかったのだけど、修正しておいた、速度vについては、これを、[km/s]の単位で読めばよろしい、某ペディアに掲げてある平均軌道速度1.022[km/s]と、なかなかよく一致しているではないか、角速度の方は、[(rad)/s]という次元なので依然として判りにくいものの、1日当たりの移動角度にすれば、13.18度、とのこと、依然として(笑)、よくわかったのやら、わからないのやら、わからない数値ではあるが(笑)。