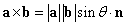
ただし、nは、
- aベクトルとbベクトルの始点をそろえ、
- aをbに重なるように回転したとき、
- その回転方向を右ねじの回転方向に見立てたならば、右ねじが進行する方向の単位ベクトル、
同一の点Oを原点とする2つの座標系S,S'があり、S'系はOを通る定軸の回りを角速度ωで、S系に対して相対的に回転している。
ここに「角速度ベクトル」ωは、
- その大きさがω、
- その回転方向を右ねじの回転方向に見立てたときに、右ねじの進行方向をその方向とする
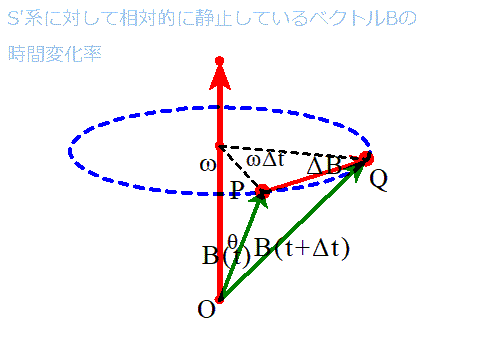 |  |
| S'系に対して相対的に静止している ベクトルBの時間的変化率dB/dt | 一般のベクトルAの時間的変化率dA/dt |
B(t+
 t)-B(t)=
t)-B(t)=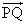
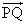 は半径Bsinθ、中心角ω
は半径Bsinθ、中心角ω tの扇形の「弦」であるが、
tの扇形の「弦」であるが、 tが十分小さいときは、「弧」に近似して差し支えない。
tが十分小さいときは、「弧」に近似して差し支えない。
したがって、
|
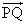 |=ωBsinθ
|=ωBsinθ t
t
また、
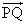 の方向は、角速度ベクトルωをBに重なるように回転したときに、右ねじの進む方向、であるから、「外積」の定義に従って、
の方向は、角速度ベクトルωをBに重なるように回転したときに、右ねじの進む方向、であるから、「外積」の定義に従って、
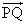 =ω×B
=ω×B t
t
すなわち、
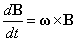
S系においては、
- 時刻tにおいてA(t)=
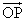
- 時刻t+
 tにおいてA(t+
tにおいてA(t+ t)=
t)=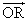
すなわち、
A(t+ t)-A(t)=
t)-A(t)=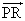
- A'(t)=

 tの間にPはQ間で移動するから、
tの間にPはQ間で移動するから、
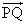 +
+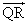 =
=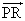
すなわち、
(ω×A) t+A'(t+
t+A'(t+ t)=A(t+
t)=A(t+ t)-A(t)
t)-A(t)
S系における変化量を A、S'系における変化量を
A、S'系における変化量を 'Aと書くと、
'Aと書くと、
(ω×A) t+
t+ 'A=
'A= A
A
よって、
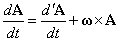 ・・・(1)
・・・(1)
 であるから、
であるから、
S系における時間変化率も、S'系における時間変化率も等しくなるので、下のような記号で定義する。
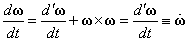 ・・・(2)
・・・(2)
- (1)の両辺をtで微分する。積の導関数(uv)'=u'v+uv'を用いて、
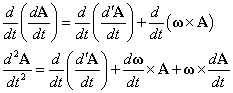
- 右辺第一項、第三項に(1)を適用して、
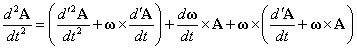
- (2)を用いてまとめると、
 ・・・(3)
・・・(3)
-
外力をFとすれば、
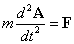 ・・・(4)
・・・(4)
-
(3)(4)より、
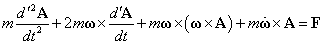
したがって、S'系における運動方程式の右辺には4つの項が現れることになる。
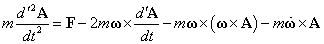 ・・・(5)
・・・(5)
- 一様な回転(ωは一定)であるから、
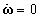 ・・・(6)
・・・(6)
- 重力mgと外力Fを受けているとして、S系での運動方程式を書くと、
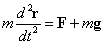
(5)の関係を用い、かつ(6)であるから、
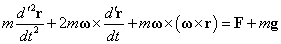
- したがって、S'系での運動方程式は、
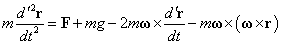
まとめると、
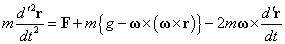 ・・・(7)
・・・(7)
右辺第2項は、「見かけの重力」であり、第3項が「コリオリの力」である。
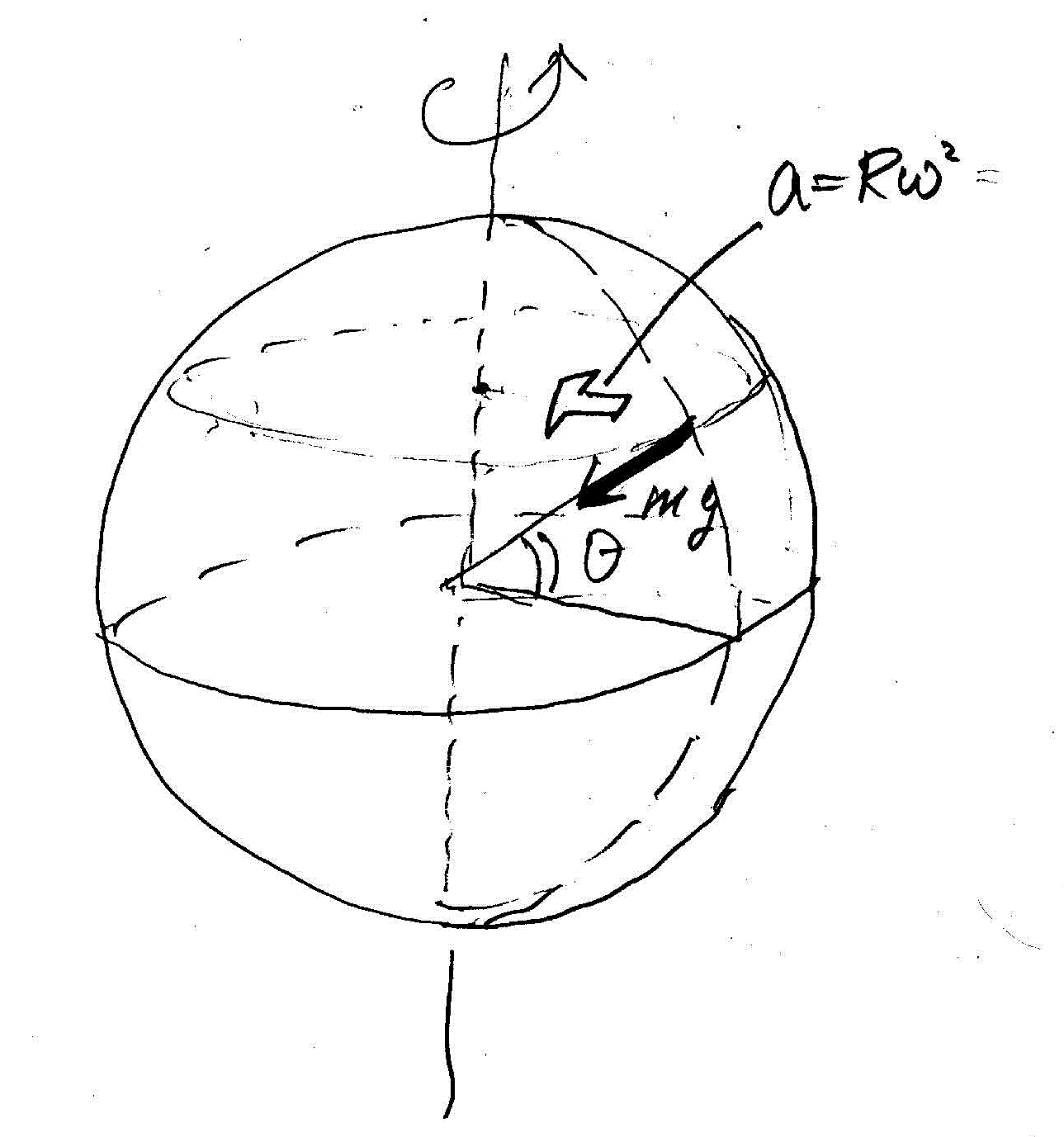 |  |  |
| 北緯θの地表面に静止している質量m質点には、地球の自転による「向心加速度」が生ずる。 | 地球の地軸に固定された観測者から見ると、この質点に作用する重力mgと、垂直抗力Nの合力が地軸に向かって垂直になっていなければならない。 | 地表面の観測者からみると、重力、遠心力、垂直抗力の3力がつりあっていなければならない。 |
| いずれにしても、垂直抗力は、地球の中心より、やや下方に向かうことになる。 | ||
 | 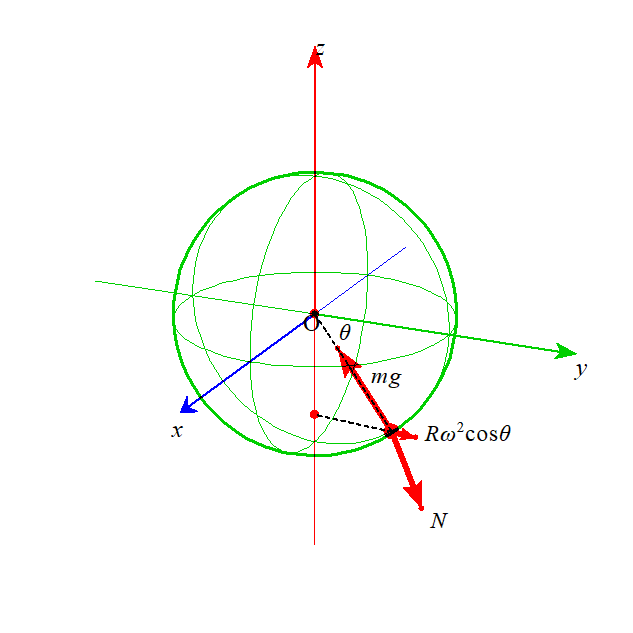 |
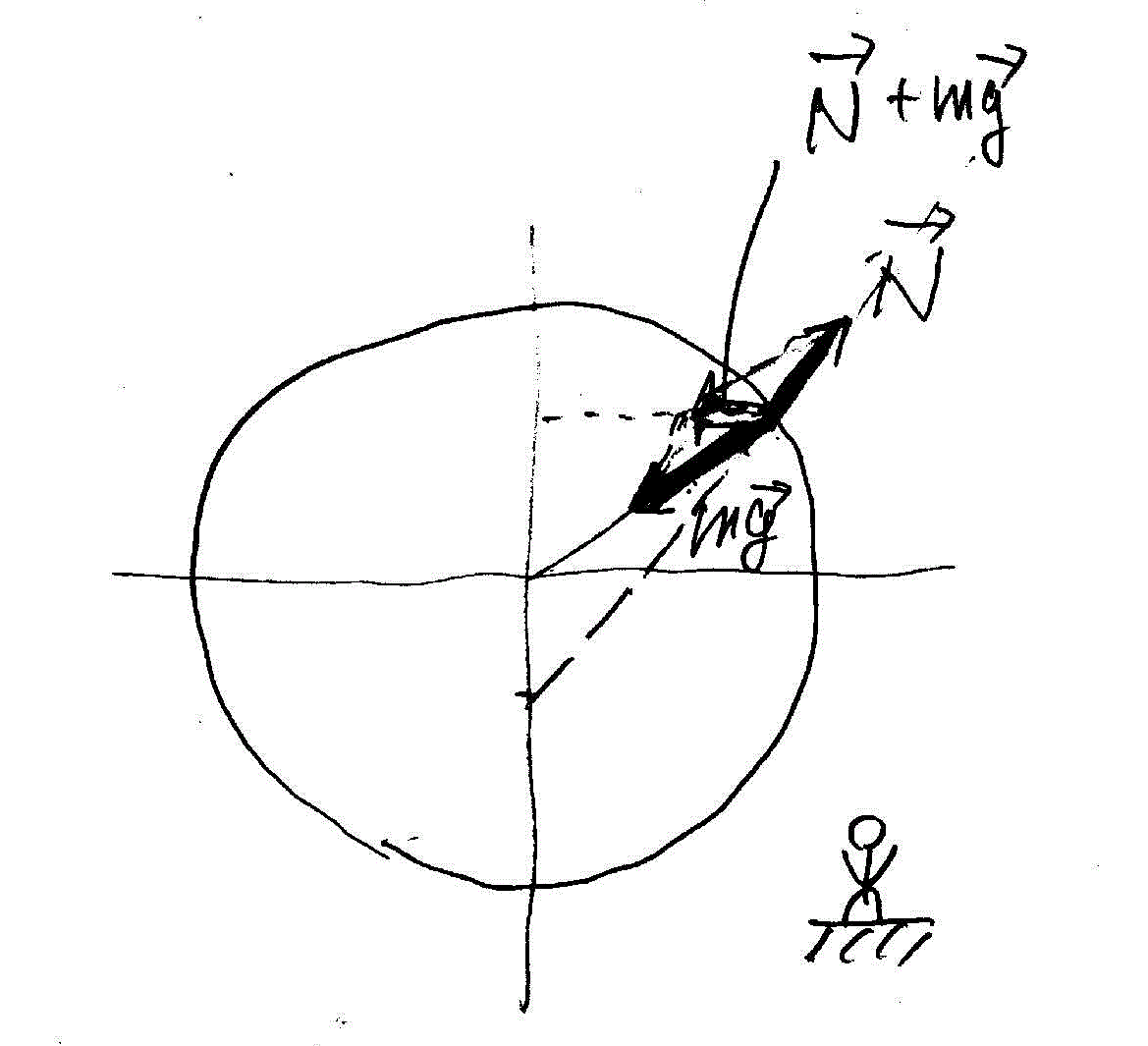
| 北緯θの地表面に静止している質量mの質点に作用する、重力mg、遠心力Rω2cosθ、これらと釣り合う垂直抗力N。 その根元は、地球中心より南極側にずれる。 |
南緯θの地表面に静止している質量mの質点に作用する、重力mg、遠心力Rω2cosθ、これらと釣り合う垂直抗力N。 その根元は、地球中心より北極側にずれる。 |
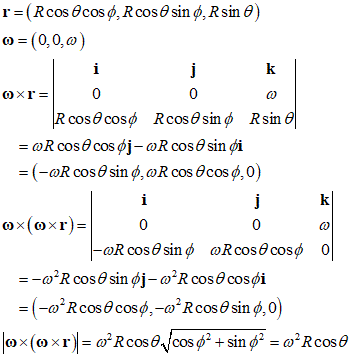

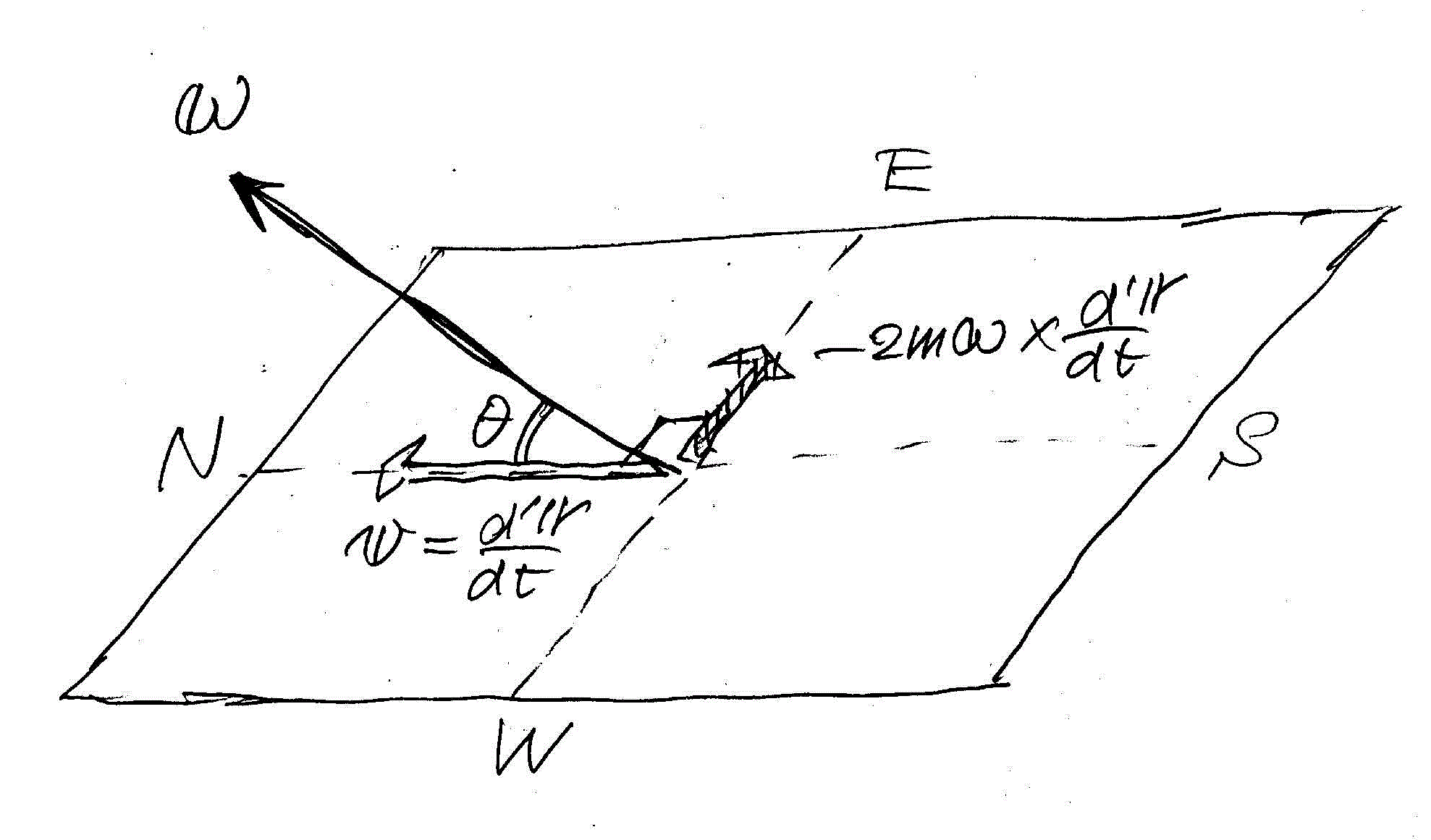
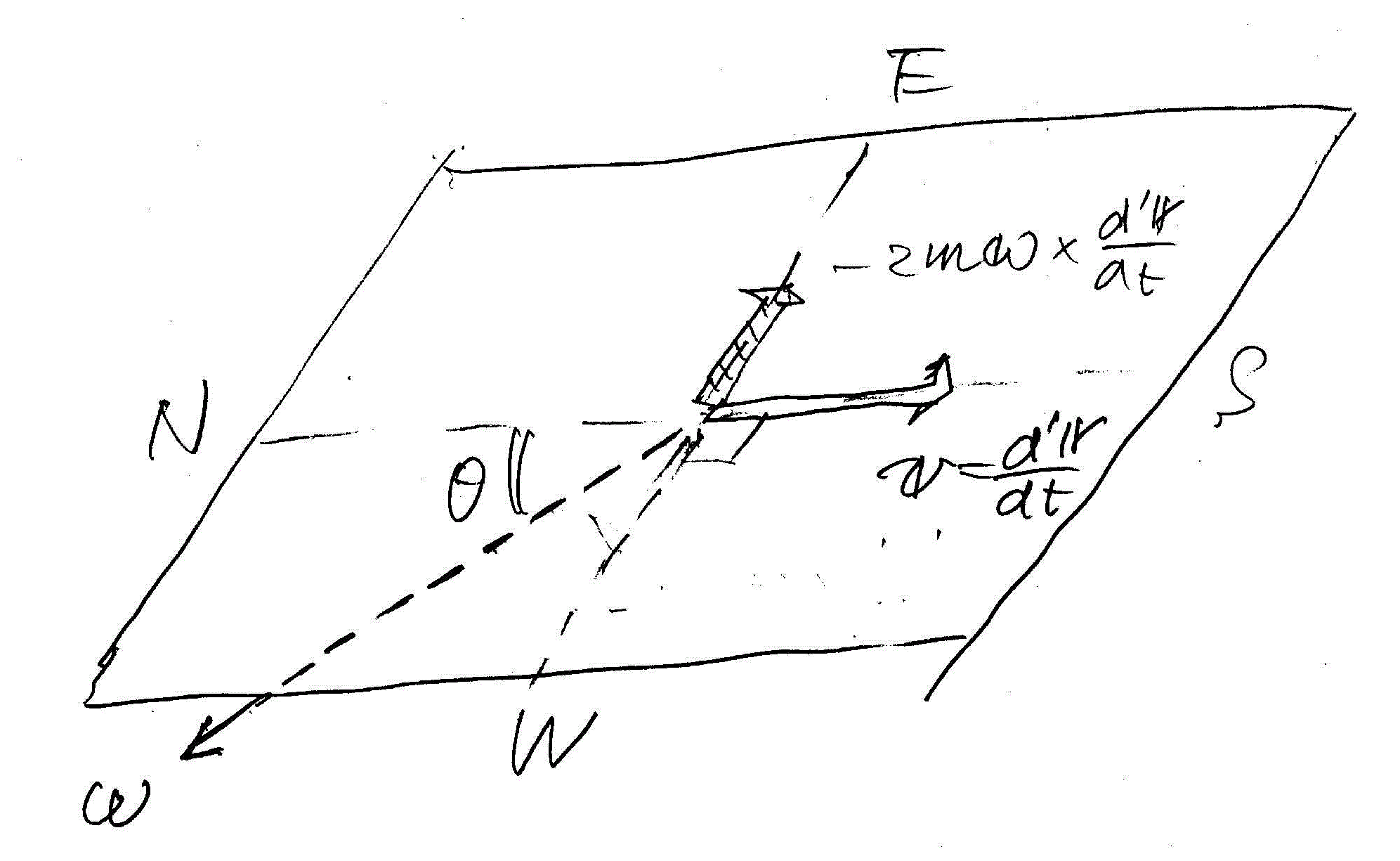
ベクトルの外積の定義に従えば、この力の方向は、
- 角速度ベクトルωを、地上の質点の移動速度ベクトルd'r/dtに重なるように回転したとき、右ねじの進む方向、
- の、反対方向、
 |  |
 |  |
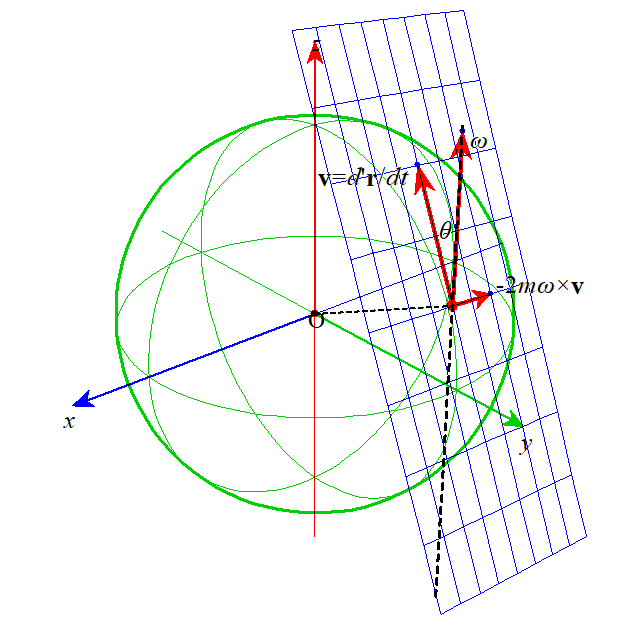 | 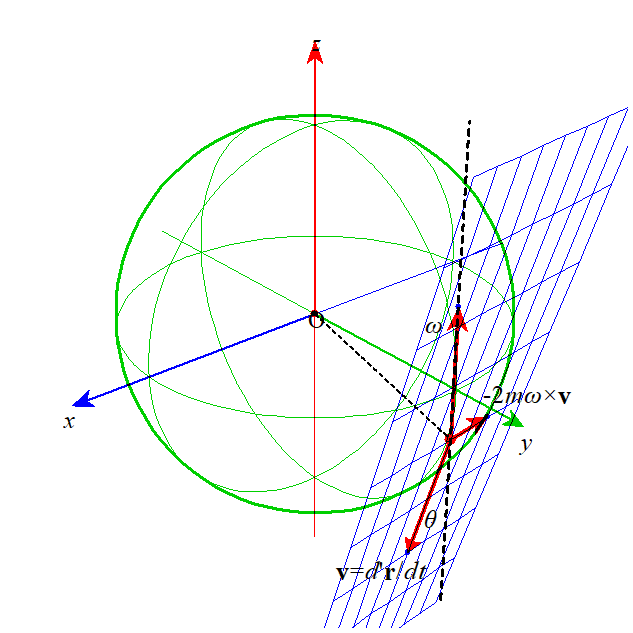 |
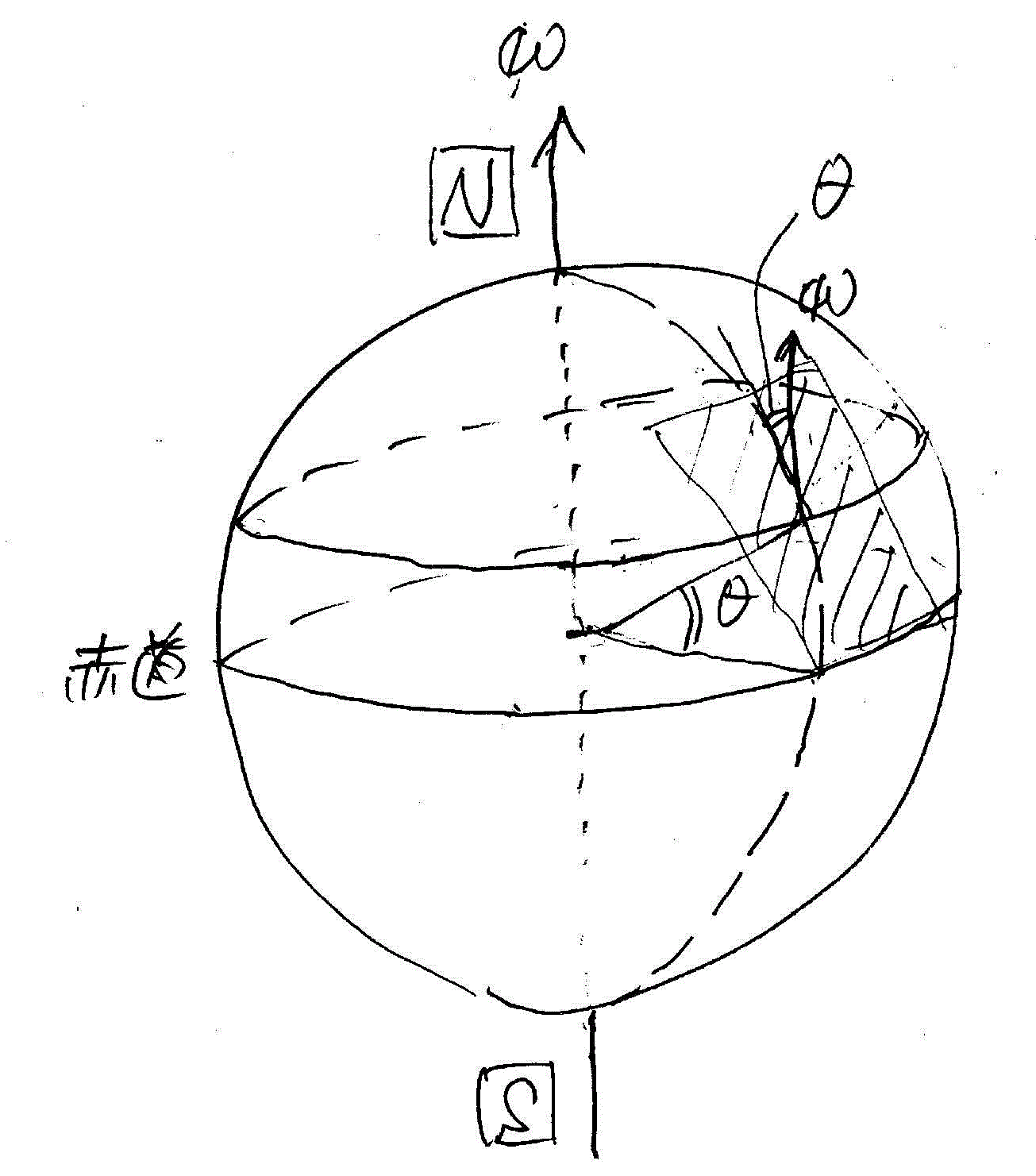
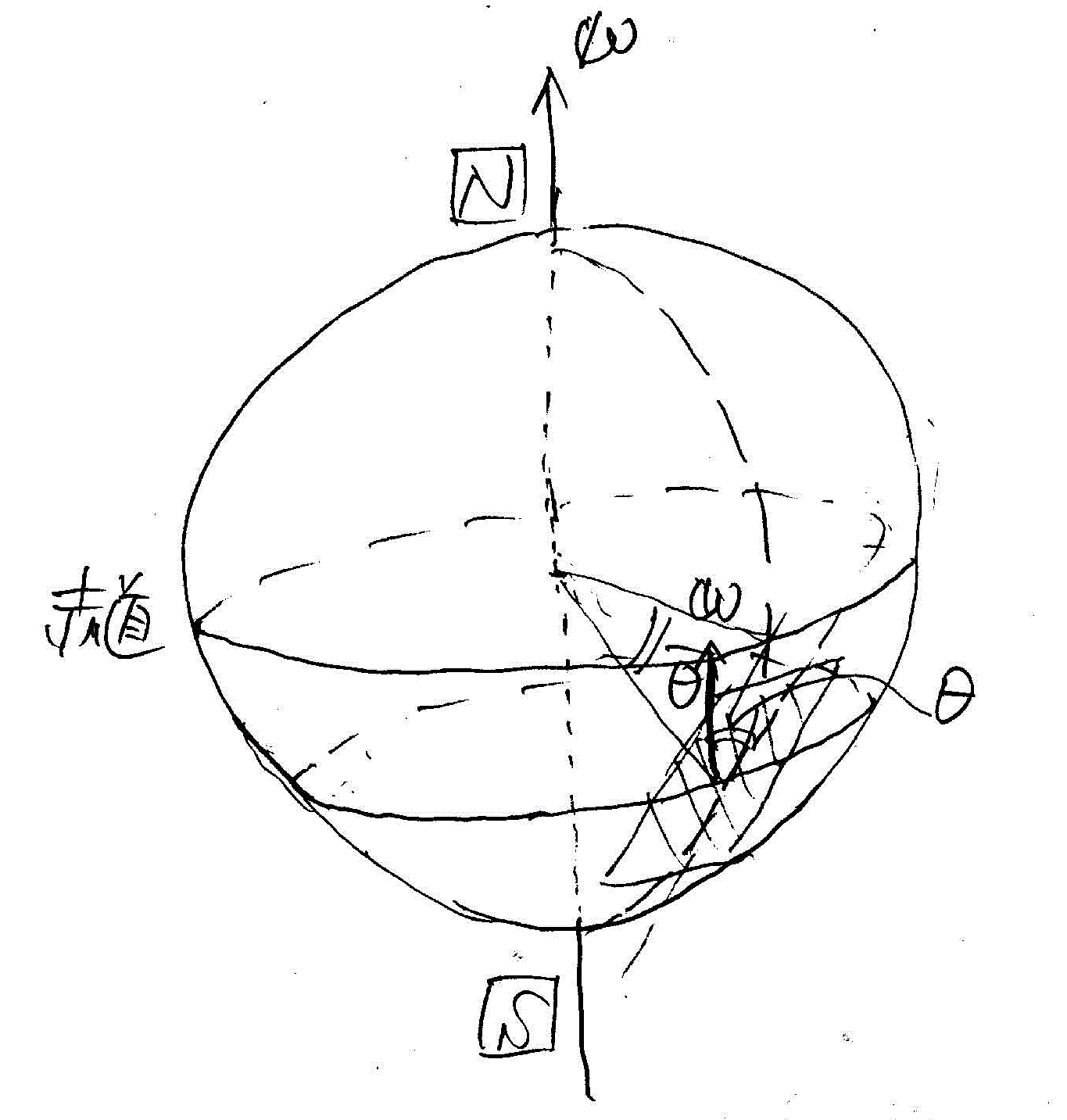
| 北緯θの地表面で、真北に向かって移動する質点には、東向きに、すなわち、進行方向に対して右に傾くように、「コリオリ力」が作用する。 | 南緯θの地表面で、真南に向かって移動する質点にも、やはり東向きに、すなわち、進行方向に対して左に傾くように、「コリオリ力」が作用する。 |