• 剛体の自由度 剛体の位置を特定するには、同一直線状にない3点、A,B,Cを指定する必要がある
  したがって、3点の座標を与える、合計9個の値が必要となるが、このうち3個は、
  これら3点から、任意の2点を選んで結んだ線分の長さが、剛体の位置にかかわらず一定であること、すなわち、
  (x_A-x_B)²+(y_A-y_B)²+(z_A-z_B)²=c_AB
  (x_B-x_C)²+(y_B-y_C)²+(z_B-z_C)²=c_BC
  (x_C-x_A)²+(y_C-y_A)²+(z_C-z_A)²=c_CA
  から決定されるから、独立な座標の個数は、6個となる
  したがって、剛体が何の拘束もなしに自由に動かしうる場合、その自由度は、6、ということになる
  剛体の1点が固定されている場合は、その1点を与える座標値3個が指定されるから、自由度は、3、となり、
  同様に、剛体がひとつの軸によって固定されている場合は、その軸まわりの回転角のみが独立、すなわち、自由度、1、となる
• 回転変位に関するオイラーの定理
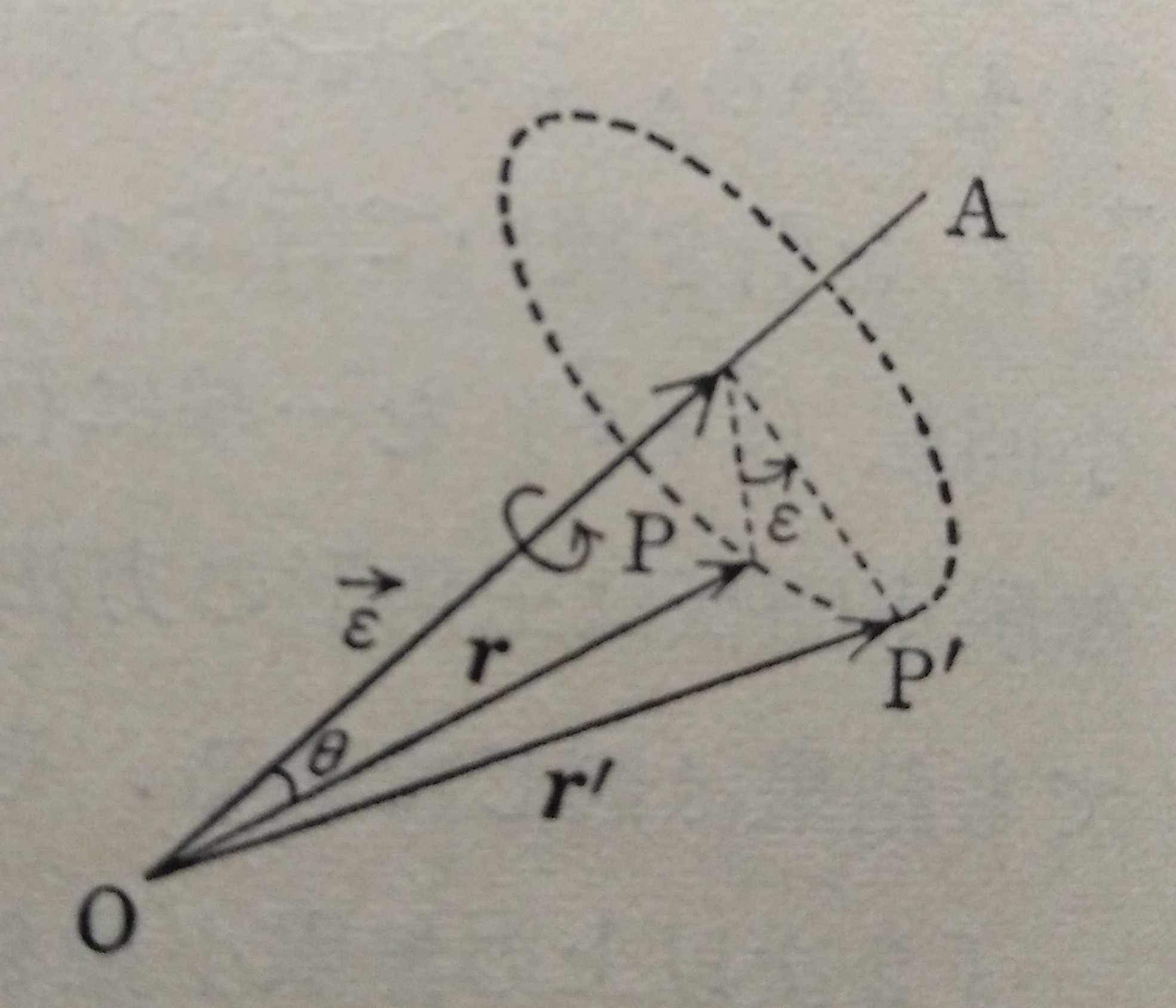
  点のまわりの回転変位は、その点を通る1つの軸のまわりの回転によって達せられる
  有限の大きさを持つ回転変位は、加法に関する交換法則が成り立たないため、ベクトルとは言えない
  しかし、無限小回転においては、近似的にベクトルと扱いうる
  
  
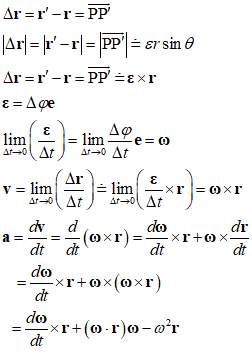
  ただし、ベクトル三重積は
  
• 運動量の法則（運動方程式）
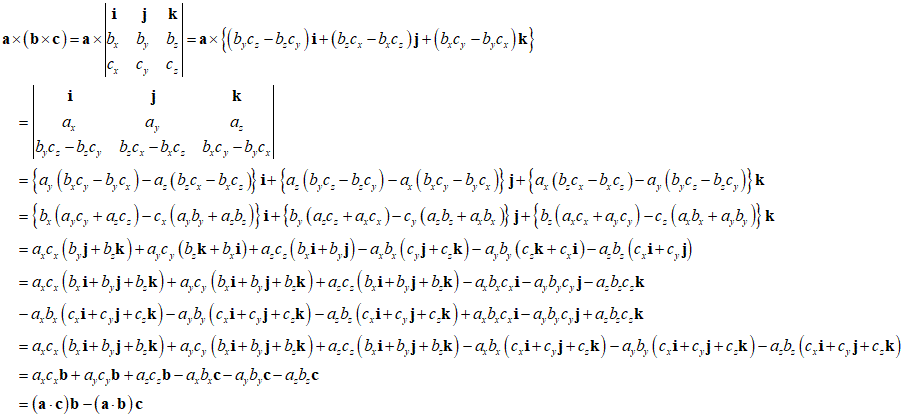
  角運動量の法則（ある時刻における質点の角運動量の時間的変化の割合は、その時刻に質点に作用する力の、原点に関するモーメントに等しい）
  
• 慣性モーメント、慣性乗積
  
• 剛体に固定され、その角速度ωで回転する座標系に対する時間微分をd'/dtで表す
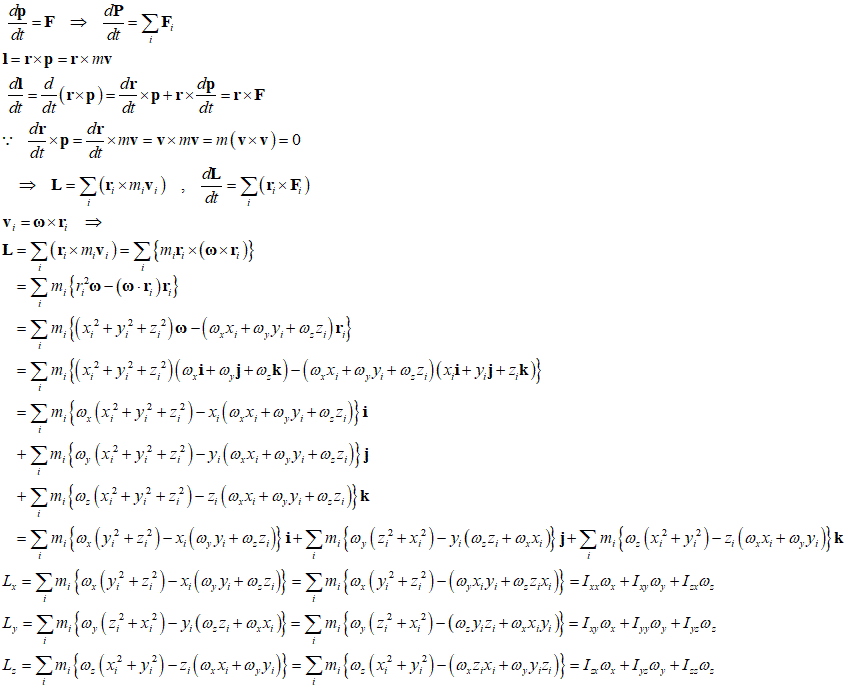
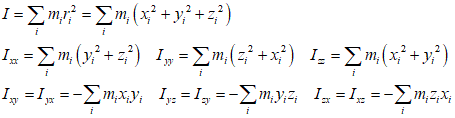
  さらに、「慣性主軸」を座標軸に取れば、慣性乗積はすべて0となるので、ここから「オイラーの運動方程式」が得られる
  
• 歳差運動
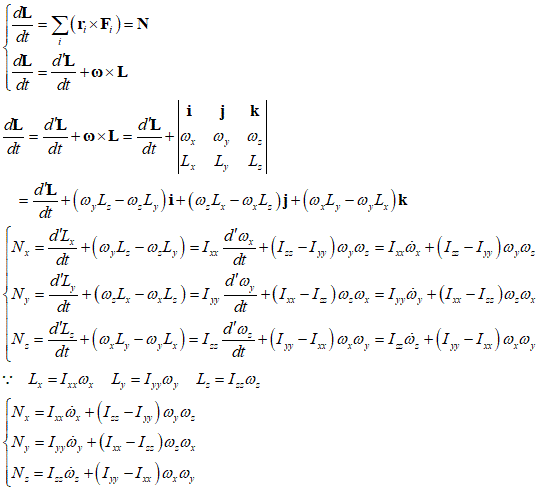
  対象軸上の固定点に関する外力のモーメントNが0である場合、かつ、剛体の対称軸をz軸にとれば、
  I_xx=I_yyである
  また、第3式から、ω_zが定数であることがわかるので、これをnとおき、また、βを次のように定めると、
  
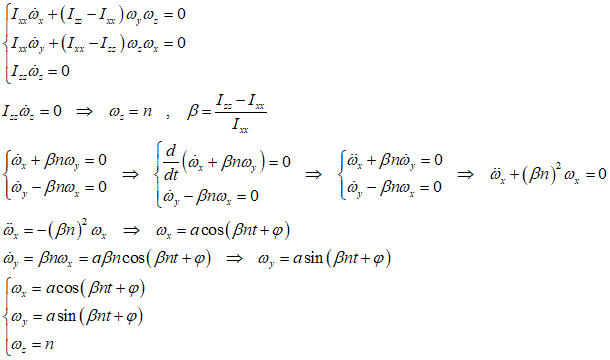
  すなわち、角速度ベクトルωの終点は、z軸に垂直な平面内の半径aの円周上を、一定の角速度βnで回転することがわかった、これを「歳差運動」と呼ぶ