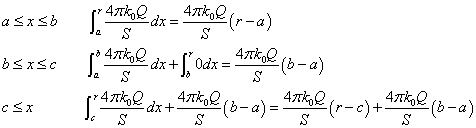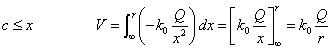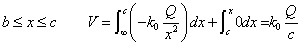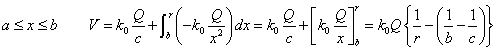• [問題]
  
• 正電荷は互いに反発するから、「導体球」の表面に等間隔に配置し、したがって球の表面に対して垂直に電気力線が
  4πk₀Q=Q/ε₀
  本が、導体球の「外」に向かって延びることになる。
  
• 「中空導体球」の内側表面には静電誘導により、負の電荷（自由電子）-Q[c]が集められ、 外側表面には、正の電荷（自由電子の不足）+Q[c]が集められ、
  内側の「導体球」から出た電気力線は、「中空導体球」内側の負電荷に「吸収」されたのち、「中空導体球」外側の正電荷から、ふたたび、同じ数だけ、発生することになる。
  これは、二つの球体の間の「真空」部分の存在にかかわらず、「同じ」電気力線が、延び続けている、と考えてもよいことを意味する。
  
• こうして、電気力線「総」本数は、r=a,r=b,r=cいずれの地点でも変わらないから、
  各地点での「電場」の強さは、電気力線「総」本数をその地点での表面積で割った、次の値になる。
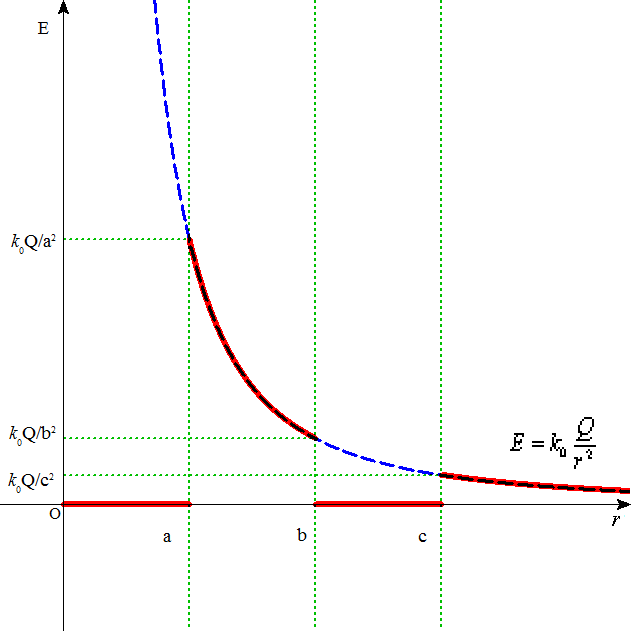
  • r=a地点・・・E=k₀Q/a²=Q/(4πε₀a²)[N/c=V/m]
  • r=b地点・・・E=k₀Q/b²=Q/(4πε₀b²)[N/c=V/m]
  • r=c地点・・・E=k₀Q/c²=Q/(4πε₀c²)[N/c=V/m]
  この計算は、中央の「導体球」の中心に+Q[c]の「点電荷」が置かれている場合とまったく同じである。
  ところが、同符号電荷はかならず金属表面に配置するから、電気力線は、金属表面の「負電荷」で終わり、金属表面の「正電荷」からふたたびはじまる。こうして、金属内部には、電気力線は発生しない、すなわち、金属内部には「電場」がないことが分かる。 。
  
  
  • 下のグラフの「破線」は、中央の球体の中心にQ[c]の「点電荷」が置かれている場合のまわりの空間の「電場」の様子を、
  • 下のグラフの「実線」は、金属内部に「電場」がないことを考慮した、まわりの空間の「電場」の様子を、
  それぞれ表している。
  
  
  
  
  
  
  
  
  
  
  
• 「電位」[V]は、「電場」[N/c=V/m]を基準面（無限遠点）からの距離で積分したもの、であるから、
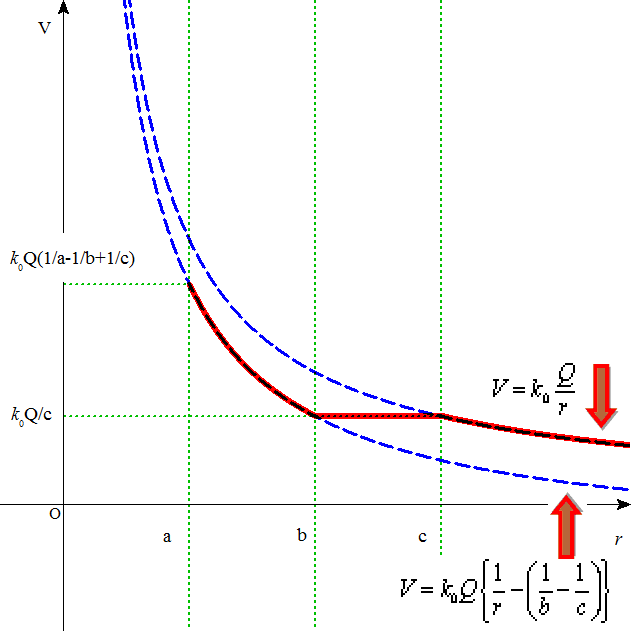
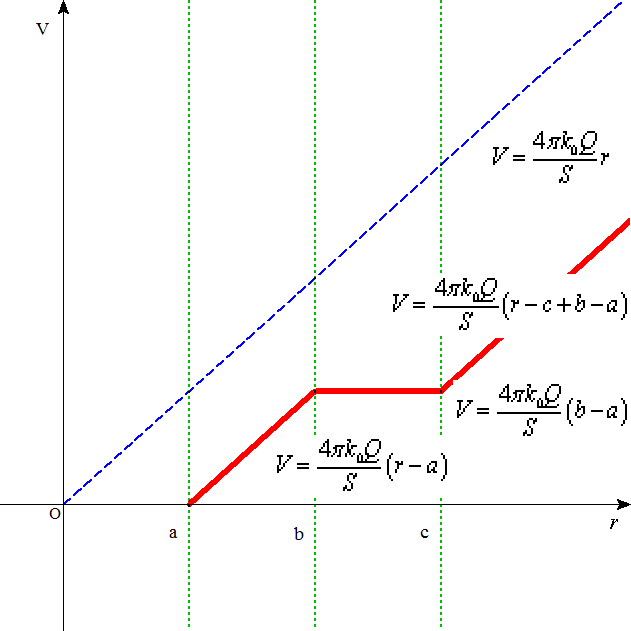
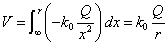  それぞれの領域での「電位」をあらわす式は、
  • 
  • 
  • 
  
  
  
  • 上のグラフの「破線」は、中央の球体の中心にQ[c]の「点電荷」が置かれている場合のまわりの空間の「電位」の様子を、
  • 上のグラフの「実線」は、金属内部に「電場」がないことを考慮した、まわりの空間の「電位」の様子を、
  それぞれ表している。
  
  
  
  
  
  
  
  
  
  
  
  
• 比較のために「一様電場」となる、別の例で考えてみよう。
  
  マイナス無限大からr=aまで、断面積S[m²]の金属柱、そのr=aの表面が+Q[c]の正電荷で帯電されており、
  プラス無限大地点にやはり断面積S[m²]の金属があって、それが-Q[c]の負電荷で帯電されていて、
  途中、r=bからr=cの区間に帯電されない、やはり断面積S[m²]の金属板が置かれている、としよう。
  
  
  
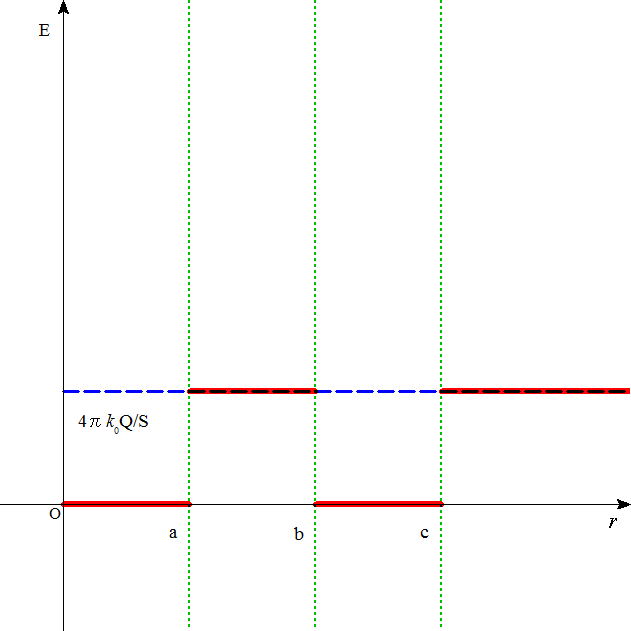
  • 断面積Sを貫く電気力線本数は、4πk₀Q本、
  • したがって、「電場」の大きさは、どこでも、E=4πk₀Q/S[N/c=V/m]
  • 上の場合と同様、金属内部には「電場」は、ない。
  
  
• これを、今度は基準面をx=0地点として、距離で積分していけば、「電位」が計算できることになる。