抵抗による減衰のある「LC振動回路」(20110820)

LC振動回路
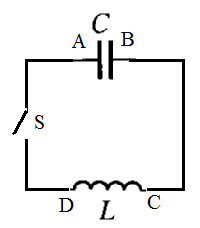
- 時刻t=0に、コンデンサのA極板に+Q₀[c]、B極板に-Q₀[c]、を蓄えてスイッチを入れる。
- 時刻tにおけるコンデンサのA極板の電荷をQ[c]、コイルをDからCに向かって流れる電流をI[A=c/s]とすると、 (電流は、正電荷が極板から「流出」する方向だから)
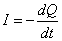  ・・・(1)
- コイルの長さl[m]、断面積S[m²]、単位長さ(1[m])当たり巻き数n₀とすると、
  - コイルが作る磁場H[N/wb]は、H=n₀I
  - コイルが作る磁束密度B[wb/m²]は、B=μ₀n₀I
  - コイル全体では、1本の磁束線がそれぞれn₀l回この磁場を横切ることになるから、コイルの全磁束Φ[wb]は、Φ=n₀lSB=μ₀n₀²lSI
  - こうしてコイルの作りだす磁束が電流に比例することから、その比例係数μ₀n₀²lSを「自己インダクタンス」Lと呼ぶことにした。
  - したがって、Φ=LI
- コイルの両端に生じる誘導起電力V_L[V](Dを基準にしたCの電位)は、
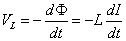  ・・・(2)
  (1)(2)より、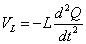
- キルヒホッフ第２法則より、V_C-V_L=0、すなわち、
  
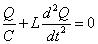
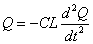  ・・・(3)
  こうして、時間の関数Qは、その2階微分が関数自身に比例し、符号が逆であるから、「単振動」を行うことがわかった。
- 時刻t=0で、Q=+Q₀であること(初期条件)から、
  Q=Q₀cosωt
  とおくことができる。これを2階微分すると、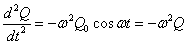
  
  であるから、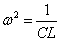   すなわち 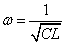     [(rad)/s]
  したがって、振動の周期は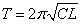   [s]である。
- よって、コンデンサのA極板の電荷Q[c]をあらわす式は、
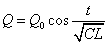     ・・・(4)
  
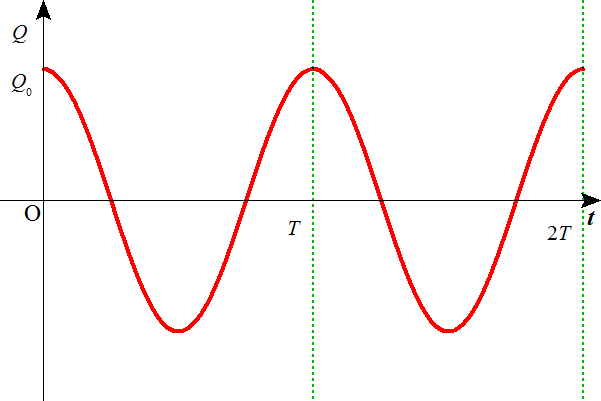
  また、コイルをDからCに向かって流れる電流I[A]をあらわす式は、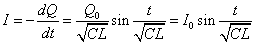
     ・・・(5)
  ただし、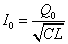
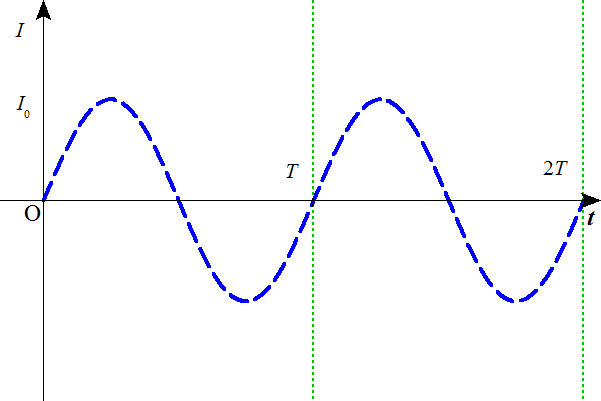
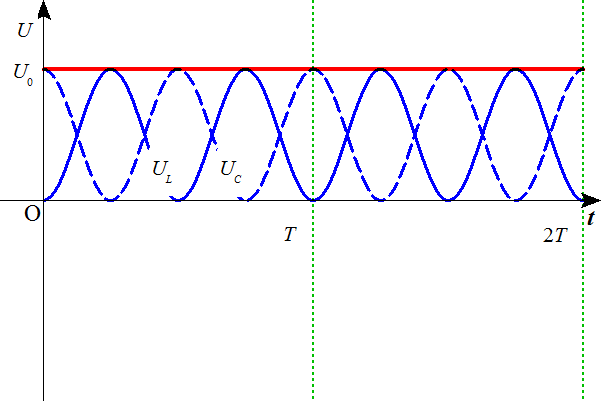
- 次に、コンデンサとコイルとのエネルギーのやり取りについて考える。
  コンデンサに蓄えられる静電エネルギーU_C[J]は、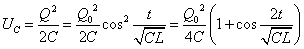
  
  t=0のとき、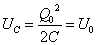   であるから、「エネルギー保存則」より、コイルが蓄えるエネルギーU_L[J]は、
  
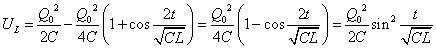
  ここで、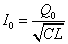   すなわち、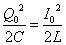   であるから、
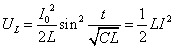
- コイルが蓄えるエネルギーU_L[J]の式は、別の方法でも導ける。
  [J=V・C=V・A・s]であるから、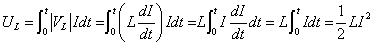
  
  最後の変形は、「置換積分」0tt→0IIを用いている。
- 以上から、「LC振動回路」のエネルギー保存の式は、
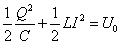  ・・・(6)
- ここに抵抗を接続すると、コンデンサ、コイル間の電荷の移動のたびごとに「ジュール熱」が発生し、これによって全エネルギーが減少するから、振幅が次第に小さくなる「減衰振動」となるはずである。
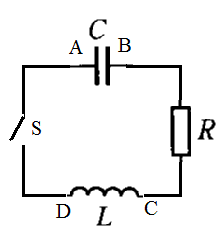
  - キルヒホッフ第2法則は  V_C-V_L-V_R=0  と変わり、
    
    
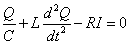
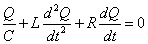
    この微分方程式を解くのは、困難であるから、以下では、1周期の間は振幅の減衰が生じず、各周期の初めに不連続的に減衰が起こると仮定する。
- 第n回めの振動の初めの電流Iの振幅がI_nであったとする。
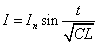     (n=0,1,2,・・・)
  この1周期に抵抗Rで消費されるエネルギーU_nは、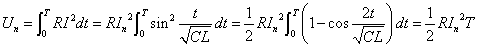
     ・・・(7)
  ただし、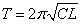
  こうして、抵抗によるエネルギー消費を考慮すると、(5)式は、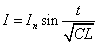
  
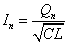     であるから、(4)式は、
  
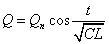
  さらに、全エネルギーをあらわす(6)式は、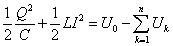
  
  となる。
- では次に、Q_n、I_nについての「漸化式」を求めてみよう。
  各周期のコンデンサ、コイルが蓄えるエネルギーの「最大値」はそれぞれ、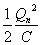
  
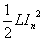
  であるから、次の周期ではこれらがそれぞれ、U_nだけ減少している。よって、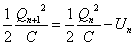
     ・・・(8)
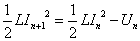     ・・・(9)
  (7)(8)より、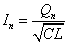   であるから、
  
  
  
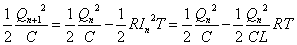
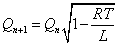
  (7)(9)より、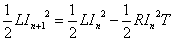
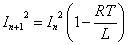
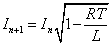
- このようにして、振幅が等比数列的に減少していく「減衰振動」であることが分かった。
  ここでは、1周期の間は振幅が変わらず、周期の変わり目で「不連続的」に減衰が生じるかのように扱った。もちろん本当は、「連続的」に変化する筈だ。
  「等比数列」を連続関数化すると、「指数関数」であることから、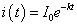
  
  とおき、
     ,
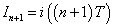
  を満たすように定数kを定めよう。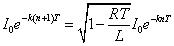
  
  
  
  
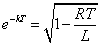
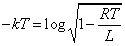
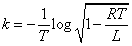
  よって、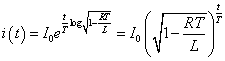
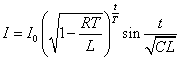
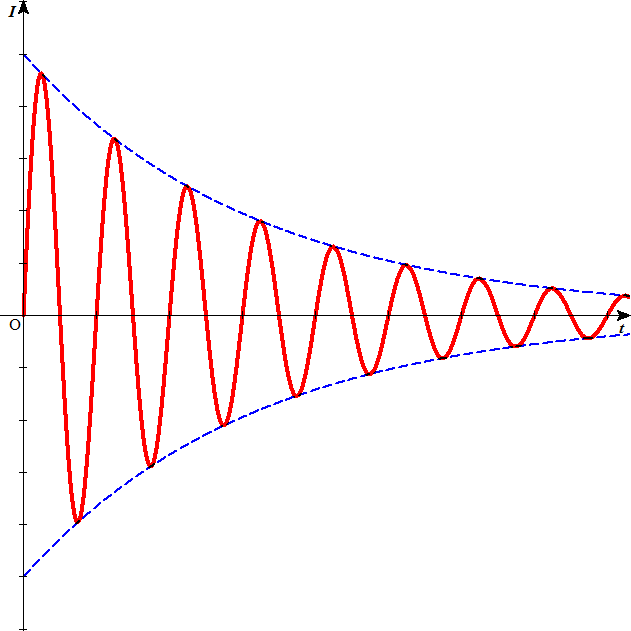
- このように、「減衰振動」とは、振幅が等比数列的に減少、すなわち、振動のグラフを包む線（「包絡線」という）が底が1より小さい指数関数であるような振動である。
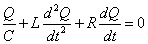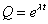【参考】この微分方程式（定数係数線形2階斉次微分方程式）を解いてみると・・・
・・・(*)
- と、解の形を仮定する。
- 1階微分、2階微分して、
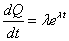
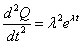
- (*)に代入すると、
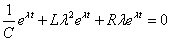
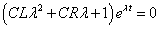
- e^λt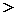0だから、
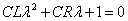
- 抵抗Rはそれほど大きくない、と思われるから、この2次方程式（特性方程式）の判別式は負になるとして、
  
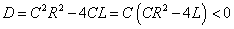
  したがってλは次のような共役複素数解となる。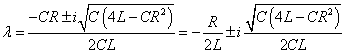
  
  これらを、λ₁  ,  λ₂とおくことにする。
- ところで、複素変数では、指数関数と三角関数との間に次のような重要な関係があることが知られている。
  
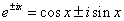
  これは、以下の「マクローリン展開」を、それぞれ指数関数、三角関数に適用してみると、理解できる。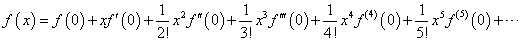
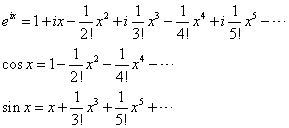
- したがって、
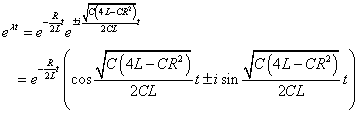
- e^λ₁t  ,  e^λ₂tが(*)の解であるならば、それらを定数倍して「重ね合わせ」たものも解であることが知られている。
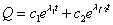
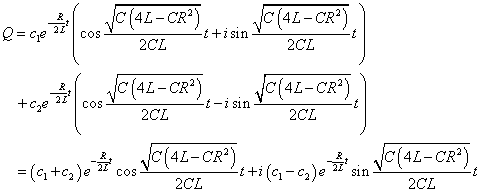
- c₁+c₁=Q₀  ,  c₁-c₁=0となるように、虚数部がゼロになるように、選ぶこともできるから、
  
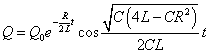
  こうして、抵抗による減衰のある単振動の式が得られた。抵抗の影響によって、周期は少し小さい値になっているが、時間の経過とともに、振幅が次第に小さくなっても、一定の周期であることに注目。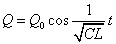
- 以下の図で破線は、抵抗による減衰のない場合、実線は、抵抗による減衰のある場合を示す。この図では周期の変化はほとんど検出できない。
  
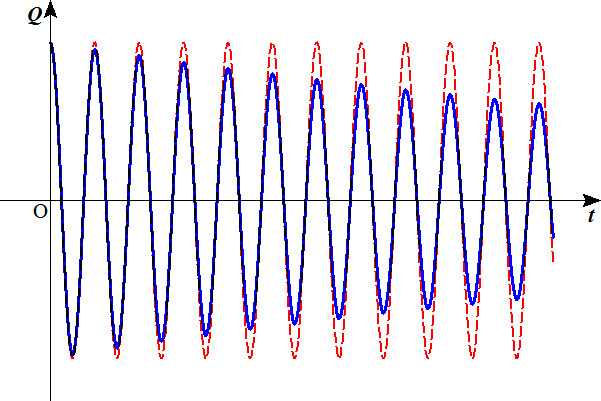
  抵抗が小さい場合
  
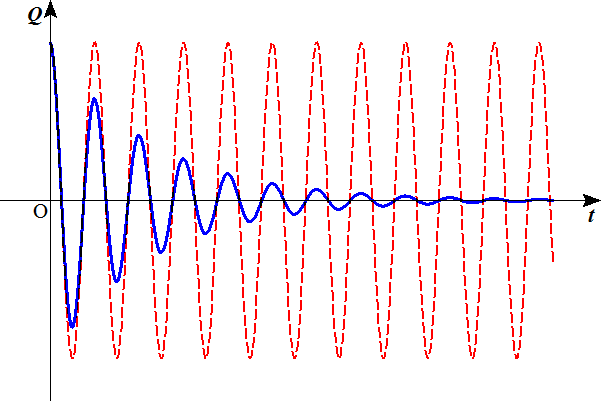
  抵抗が大きい場合

(2008)