(3)[エネルギー・熱の移動](2007本4c)一部
(3)[エネルギー・熱の移動](2007本4c)一部
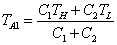

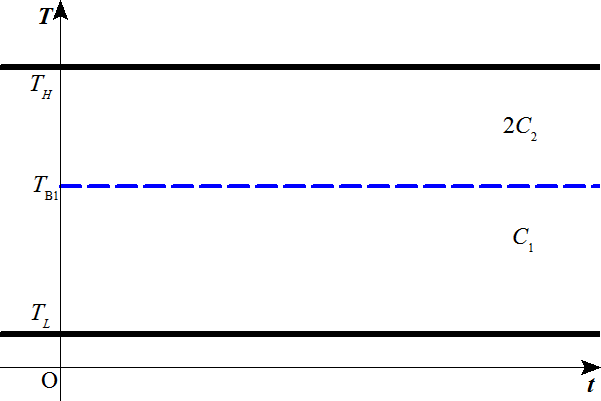
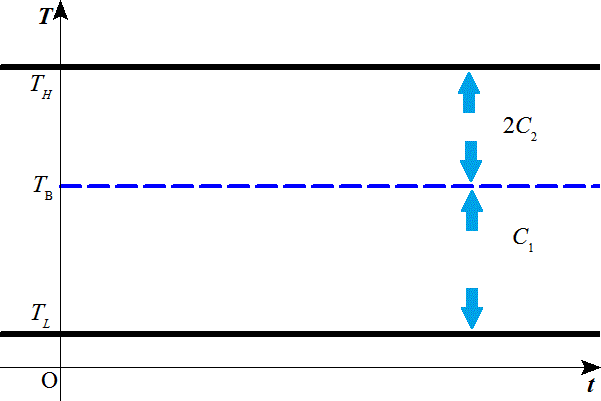
 C1(TH-TB1)=C2(TB1-TL)
C1(TH-TB1)=C2(TB1-TL)
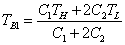
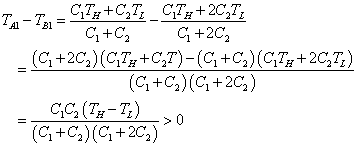
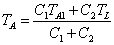
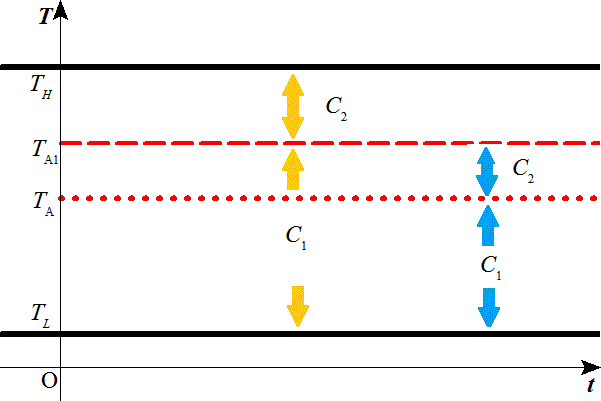
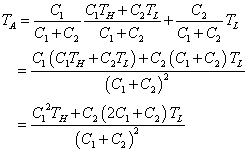
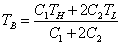
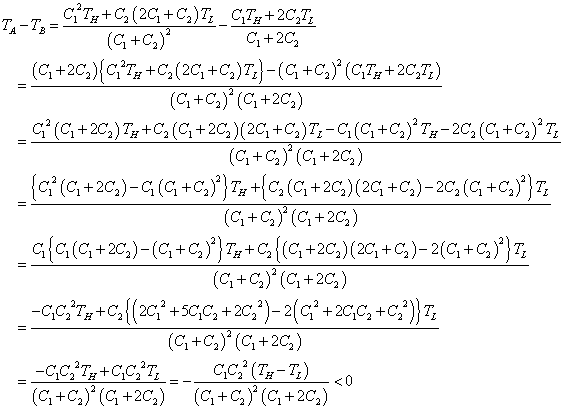

 T=TH-TL
T=TH-TL
 TA=TA-TL
TA=TA-TL
 TB=TB-TL
TB=TB-TL
 TAは、
TAは、 Tを
Tを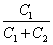 倍に縮小した後、再び、
倍に縮小した後、再び、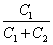 倍に縮小したもの
倍に縮小したもの
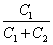 )2倍に縮小したものだ。
)2倍に縮小したものだ。
 TBは、
TBは、 Tを、ただ一度だけ、
Tを、ただ一度だけ、 倍に縮小したものだ。
倍に縮小したものだ。
 TA=(
TA=(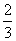 )2
)2 T=
T=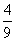
 T
T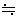 0.44
0.44 T
T
 TB=
TB=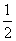
 T=0.5
T=0.5 T
T
 TA=(
TA=(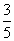 )2
)2 T=(9/25)
T=(9/25) T=0.36
T=0.36 T
T
 TB=
TB=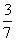
 T
T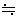 0.43
0.43 T
T
 TA=(
TA=(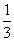 )2
)2 T=
T=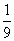
 T
T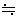 0.11
0.11 T
T
 TB=
TB=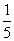
 T=0.2
T=0.2 T
T
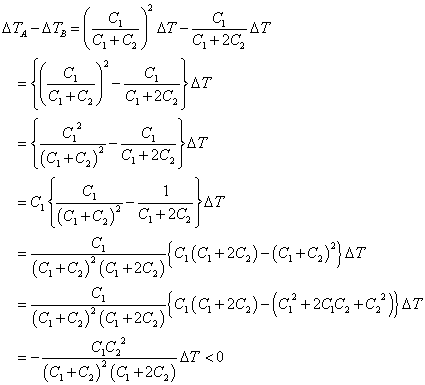


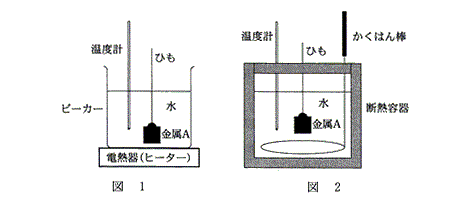
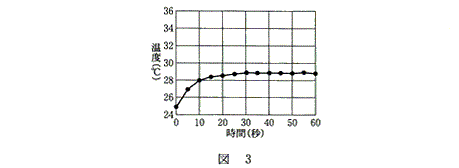

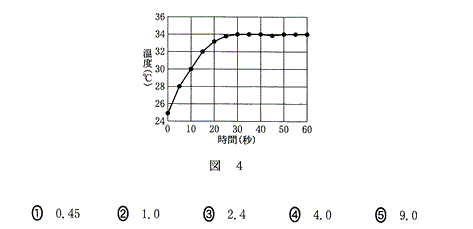
(3)(理科総合A・2009本試験第3問の一部)


