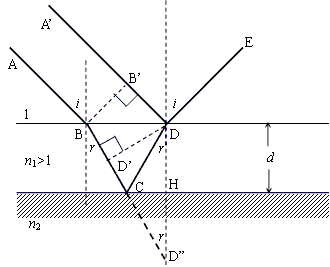
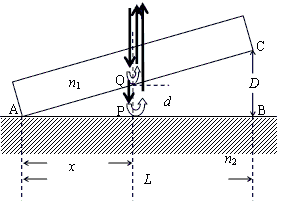
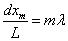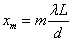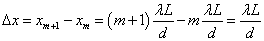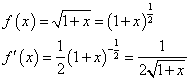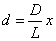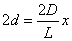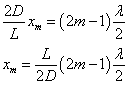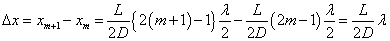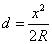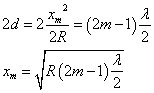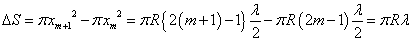- スカラー量:「大きさ」のみを問題にする量。ただし、「正負」はある。1次元の数直線に対応することができる量。
- ベクトル量:「大きさ」と「方向」を問題にする量。ただし、「位置」は問題にしない。平行移動して重なるものは、「同じ」ベクトルである。
| スカラー量 | ベクトル量 |
|
|
|
|
|
|
カッコが付けてあるのは、は物理Ⅱの内容
長さ[m]、質量[kg]、時間[s]、を3つの基本単位として、その他の単位はすべてこれらの「掛け算」または「割り算」として表現できる。3つの頭文字をとってMKS単位系と呼ぶ。電磁気学では、これに電流[A]を加える(MKSA単位系)。
例えば、「力」の単位[N]は、「運動方程式」 F=ma から
[N=kg・m/s2]
「仕事」の単位[J]は、「仕事の定義」 W=Fx から
[J=N・m=kg・m2/s2]
おもな物理法則は、「経験則」である。ほとんどが、「比例」または「反比例」という単純な数式になっている。別に不思議なことではなくて、人間はそれぐらいの単純な関係しか見抜けないからだ。
条件を変えて繰り返し実験してみたところ、ある量とある量に「比例関係」があることが「発見」された。
例えば「オームの法則」 V=IR 。電圧Vと電流Iに比例関係があるらしいことがわかった、とする。だから「比例定数」をRにした。この段階でRの「意味」はわからない。一定の電圧に対して、電流を妨げるはたらきをするようだから「抵抗」と名づけた。単位はどうするか?「比例定数」の単位には本来「意味」があるはずがない。式の両辺が「つじつまが合う」ように調整しただけだ。だから、Rの単位は、[V/A]でよかったのだが、これにこの重要な法則の発見者にあやかって新しい名前[Ω=V/A]をつけただけだ。
ところが、今度はこの「抵抗」の性質について詳しく調べていくと、同じ材質の金属を使った場合、長さl[m]に比例して、断面積S[m2]に反比例することがわかった。
そこでその「比例定数」をρとした。その単位は両辺の単位がそろうように、[Ω・m]となり、これには特に名前は付けなかった。この、オーム×メートルという単位をいくら眺めていても、この定数の「意味」は見えてこない。当たり前だ、単につじつま合わせしただけだから・・・。
さて、抵抗の持つ「属性」のうち、「長さ」でも「断面積」でもないものが、このρのなかにこめられている。それは、抵抗を作っている金属の種類、などの「材質」によるものだろう。だから、「材質」によって決まる「定数」として、「抵抗率」と呼ぶことにした。
こんな風にして「物理法則」はできていく。
「物理法則」が発見されるときは、一見全然性質が異なるものの間に「比例関係」が見つけられたりすることが多いから、「比例定数」の単位も複雑なものになる。
復元力に関する「フックの法則」
F=-kx
この場合のkの単位は
[N/m=(kg・m/s2)/m=kg/s2]
というわけのわからないものになる。
同じ性質のものの間の比例関係を扱った式では、比例係数に単位がないものもある。
動摩擦力[N]と垂直抗力[N]の比だから、動摩擦係数μ'には単位がない。
f=μ'N
では、「運動方程式」 F=ma はどうだろう?
これは、「外力と加速度は比例する、その比例係数が質量である」と、読めなくもないが、普通は、「外力」、「質量」、「加速度」という、いずれも実体のある3つの量の間の関係を表したものといえるだろう。すなわち、
「質量mの物体に外力Fが作用すると、これに比例した加速度aが発生する。」
となる。「比例係数」はどうなったのだろう?
あまりにも重要な「法則」だから、「比例係数」がなくてもすむように[N](ニュートン)という新しい「単位」を決めたのだ、ということになるだろう。
|
微分とは、『細かい割り算』のことである。
タテ軸の変量を横軸の変量で微分すると、グラフの接線の傾きが得られる。 タテ軸の変量が横軸の変量に『比例』しているという特別な場合は、別に微分と大げさに言わなくても、割り算すれば、その直線の傾きが得られる。 |
積分とは、『細かい掛け算の足し算』のことである。
タテ軸の変量を横軸の変量である区間について定積分すると、グラフより下にある部分の面積が求められる。 タテ軸の変量が定数であるという特別な場合には、別に積分と大げさに言わなくても、掛け算すれば長方形の面積が得られる。 |
|
|
|
|
『道のり』を『時間』で割れば、『速度』だ、と教えられた。
でも、正確に言うとそうではなくて、『変位』を『時間』で微分したものが、『速度』だ。 |
『仕事』は、『力』かける『移動距離』だ、と教えられた。
でも、正確に言うとそうではなくて、『力』を『変位』で積分したものが、『仕事』だ。 |
|
- [例1] 地上から真上(y方向)に質量の物体m[kg]を初速度v0[m]で投げ上げる。最高点に達する時間と、そのときの高さは?
運動方程式 -mg=ma ------------- ----------------- 加速度[m/s2] a=-g 順次tで積分すると次の式が得られる。
不定積分には「積分定数」が表れるが、
t=0のときの速度、変位の値がこれにあたる。速度[m/s] v=-gt+v0 変位[m] y=- gt2+v0t
「最高点」では、「速度」が0であることから、そのときのtを求めることができる。これを「変位」の式に代入すれば、そのときの高さがわかる。
- [例2] ばね定数kのばねに外力を加え、自然長からx0[m]まで引き伸ばした。このときばねに蓄えられた弾性力による位置エネルギーは?
ばねは、伸ばそうとすると縮み、縮めようとすると伸びる。外部から加えられた変形に対して、これを元に戻そうとする力を「復元力」という。
F=-kx (復元力に関するフックの法則:「変形を加えると、変形の大きさxに比例し、かつ、これと反対向きの力が発生する)
では、この力「弾性力」とちょうどつりあうような外力kxを加えながら、ばねの伸びが0からx0になるまで引っ張ったときに外力がする仕事は、[J]=[N・m]だから、「力」を「変位」で積分すればよい。
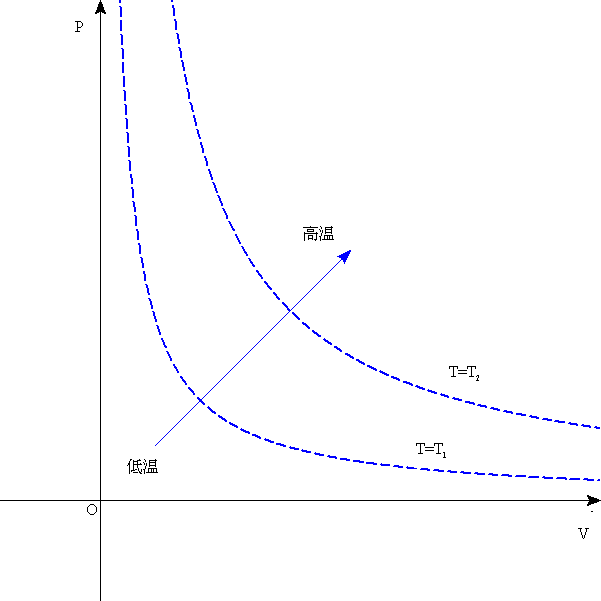
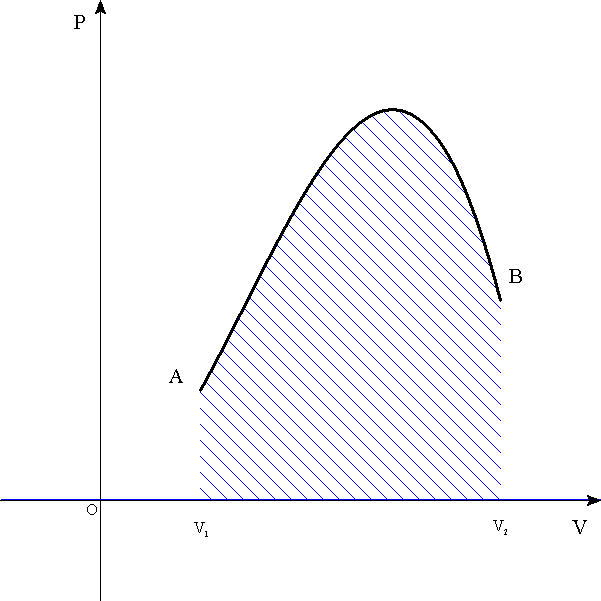
- [例3] 大気圧P0[Pa]とつねにつりあいながら滑らかに動くピストンの付いた容器に気体を閉じ込め、加熱して、体積をV1からV2に変化させた。このとき、気体が外部にした仕事は?
[J]=[N・m]=[Pa・m3] だから、気体がした仕事は、「圧力」を「体積」で積分すればよい。
ここでは「定積変化」だから、「圧力」は定数P0で、仕事は長方形の面積で表される。
| 内積(スカラー積) | 外積(ベクトル積) | |
| 定義 |
 ・ ・
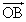 =| =| || ||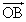 |cosθ |cosθ
ただし、θ= |
 × ×
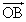 =| =| || ||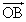 |sinθ・ |sinθ・
ただし、θ=  は、 は、 から から
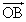 に向かって回転させたとき「右ねじの進む方向」と決める。 に向かって回転させたとき「右ねじの進む方向」と決める。
|
| 意味 |
「仕事」を定義するために考案された。
物体に力を加え移動させるとき、移動方向の力の成分しか仕事をしない。 W= 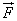 ・ ・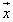 =| =|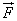 || ||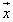 |cosθ |cosθ
|
OA,OBを隣り合う2辺とする平行四辺形の面積を表すベクトル量(面積ベクトル)。
垂直抗力NのAまわりモーメントは、 Nlsinθ=| 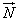 × ×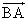 | |
|
| 例 | 仕事 | 力のモーメント、面積速度(万有引力)*、右ねじの法則(電流が作る磁場)*、フレミングの左手の法則(磁場の中の電流が受ける力)* (*は、物理Ⅱ) |
高校の数学では、「内積」しか学習しない。でも、こんな風に物理では「外積」がこっそり持ち込まれている。「数学」と「物理」は切り離すことができない。特に19世紀に進展した「線形代数学(ベクトル・行列)」は、物理学的な現象を、数式で表現するために考案されたものだ。
 t[m・s])
t[m・s])

 mv2[J]のエネルギーをもつ。
mv2[J]のエネルギーをもつ。
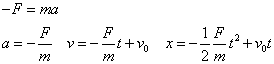
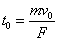
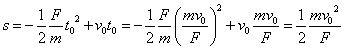
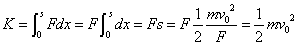
 lcosθ-N1lsinθ=0
lcosθ-N1lsinθ=0

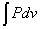
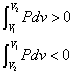
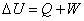
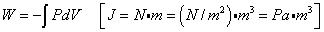
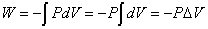
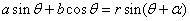
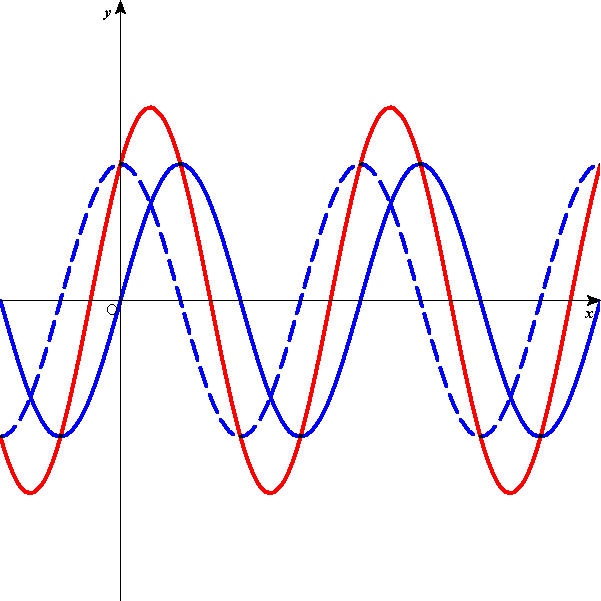
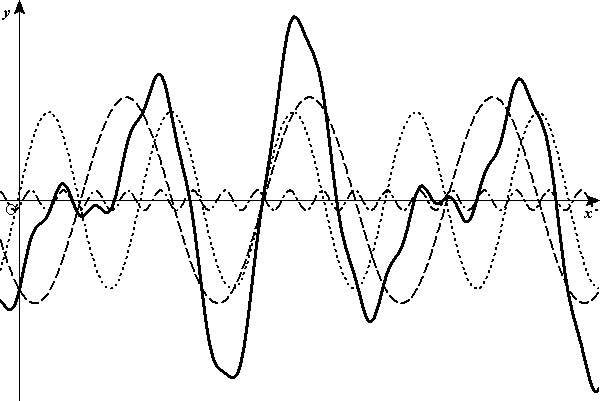
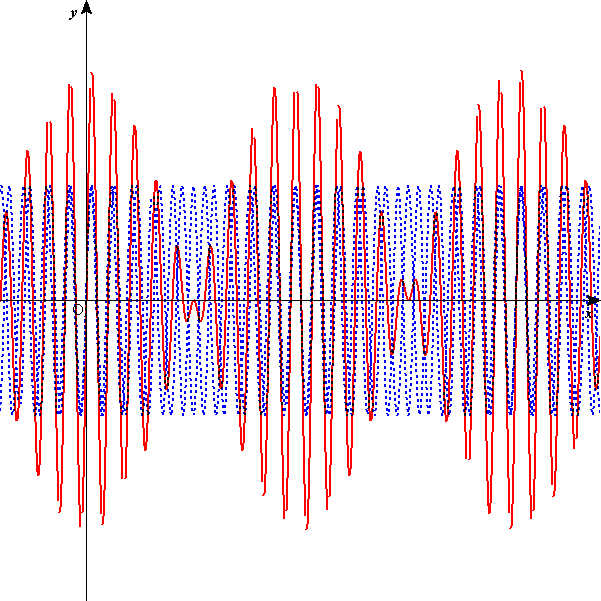
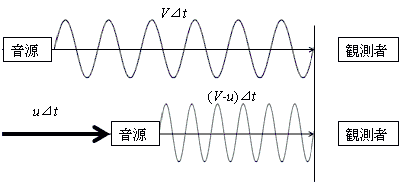
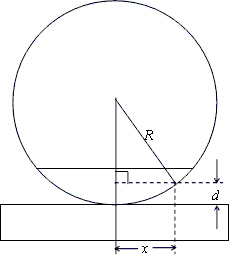
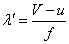 [m]
[m]
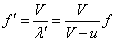 [Hz=1/s]
[Hz=1/s]
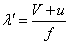 [m]
[m]
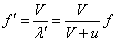 [Hz=1/s]
[Hz=1/s]
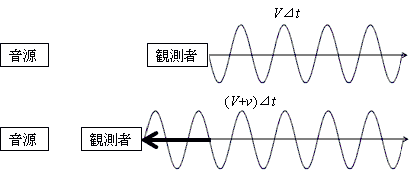
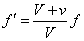 [Hz=1/s]
[Hz=1/s]
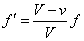 [Hz=1/s]
[Hz=1/s]
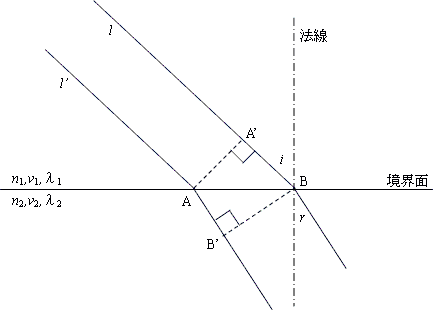
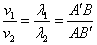
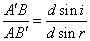
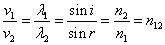
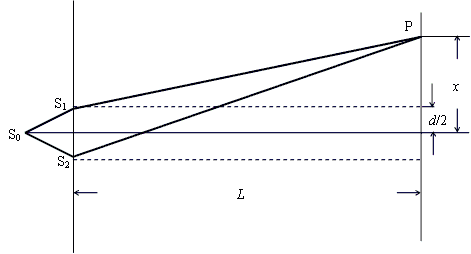
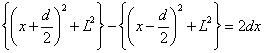
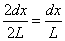
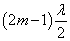 (m=1,2,3,・・・)
(m=1,2,3,・・・)