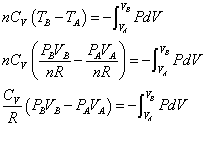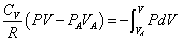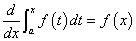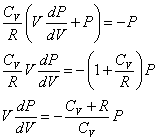一般に、「分子間力」は、分子間の距離が大きくなると、急速に小さくなる。
- 固体:分子間の距離がきわめて小さく、したがって、大きな分子間力によって相互に強く拘束されている。だから、各分子は、ほとんど動けない。
→固体には「形」が、ある。 - 液体:固体と気体の中間的な状態。
→液体の「形」は、容器の形で決まる。(容器の下に溜まるのは、重力の影響が及ぶ程度には、密度が高いからだ。) - 気体:分子間の距離がきわめて大きく、したがって、分子間力の影響がほとんど及ばない。だから、各分子は、ほぼ、「自由に」動き回ることができる。
→気体には「形」が、ない。
複雑な「分子間力」の影響を考慮せずに、比較的簡単な関係式(比例・反比例)で表現できるから、「熱力学」の研究には、「気体」が、選ばれた。
歴史的には、「産業革命」時の「蒸気機関の改良」という実用的な目的が大きかったが・・・。
- ボイルの法則
温度が一定であれば、気体の圧力と体積は、反比例する。
PV=c
- シャルルの法則
圧力が一定であれば、気体の占める体積は、温度が1 上昇するごとに、0
上昇するごとに、0 での体積を基準にして、その1/273だけ増加する。
での体積を基準にして、その1/273だけ増加する。
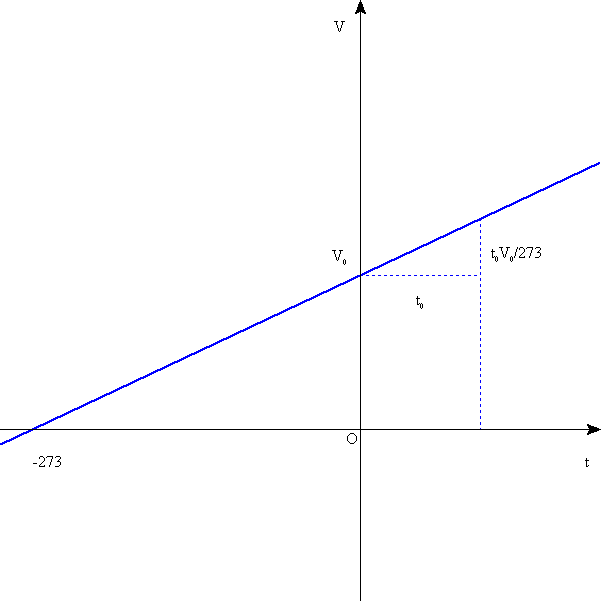
t における体積をv(t)とすると、以下のように書ける。この、原点を通らない1次関数は、何かと扱いにくいので、温度の定義を変え、これを平行移動して原点を通る比例関係にした。
における体積をv(t)とすると、以下のように書ける。この、原点を通らない1次関数は、何かと扱いにくいので、温度の定義を変え、これを平行移動して原点を通る比例関係にした。
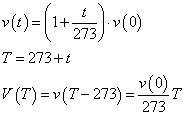
元来「摂氏・セルシウス」温度は、人間のもっとも身近に存在して、かつ容易に3態変化を示す「水」という物質の、沸点と凝固点を基準にして、これを便宜的に100等分して設定されたものである。
目盛りの幅はそのままに、摂氏マイナス273度をあらたに0度(絶対0度・単位[K]ケルビン)とすれば、
圧力が一定であれば、気体の圧力は、絶対温度に比例する、といえる。
V/T=c
従って、絶対0度では、気体は体積を持たない。もちろんこれは「理想気体」における想定であって、「実在気体」では、(1)気体分子に大きさがあり、(2)分子間力が作用するから、冷却しても、絶対0度になる以前に、「凝縮」して液化する。
- ボイル=シャルルの法則
温度が一定であれば、気体の圧力と体積は、反比例する。
圧力が一定であれば、気体の圧力は、絶対温度に比例する。
という二つの事実から、ただちに次のことが言える。
いかなる温度・圧力においても、圧力と体積の積を絶対温度で割った商の値は一定である。すなわち、

- 理想気体の状態方程式(物理II)
「アボガドロの法則」は「同温・同圧・同体積の気体には、同数の分子が存在する」ことを明らかにしている。
従って「ボイル=シャルルの法則」

の右辺は、気体の種類にかかわらず、「理想気体」の仮定から、その大きさ、形は無視しているものの、さらには気体分子の質量にも無関係に、一定の値をとることになる。
とすれば、「同数」の分子を選んでこの右辺の値を定数として定めれば便利であろう。これが「気体定数」である。
原子を構成する粒子は、陽子・中性子・電子であるが、陽子と中性子の質量はほぼ等しく、電子の質量の約1840倍である。従って原子の質量は、その陽子数と中性子数の和(これを質量数と呼ぶ)に、ほぼ比例する。
地球上に普遍的に存在する質量数12の炭素を基準として、その「原子量」を12と定めた。これを、通常の質量の単位である「グラム」と関連付けたのが、「モル」の概念である。
質量数12の炭素原子が、いくつ集まれば、ちょうど12グラムになるか?その答が、「6かける10の23乗(アボガドロ数)」であり、アボガドロ数個の粒子の集団を「モル」と呼ぶようになった。
気体の種類によらず、1モルの理想気体についてPV/Tの値が気体定数Rとして定められた。気体の分子の数がn倍になれば、たとえば体積・温度を一定に保てば、壁面に衝突する頻度もn倍になる。気体の圧力は、気体分子が単位時間に壁面の単位面積に衝突して加えた力積と考えられるから、やはり圧力もn倍になる。こうして一般にnモルの気体についての状態方程式PV=nRTが得られた。
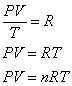
[Pa・m3]=[(N/m2)・m3]=[N・m]=[J]
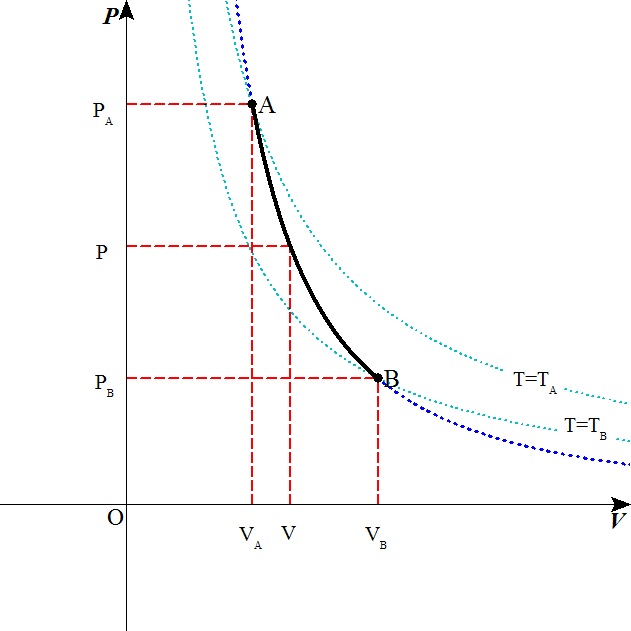
- P-Vグラフの見方
- もう一つの変数Tはどこに表されているか?
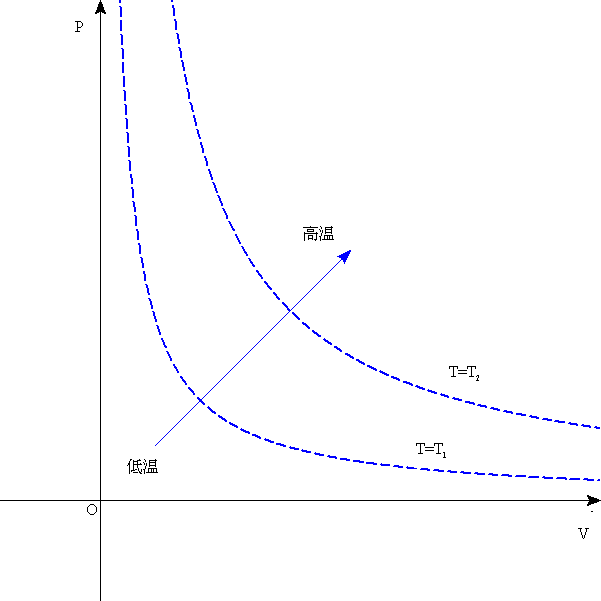
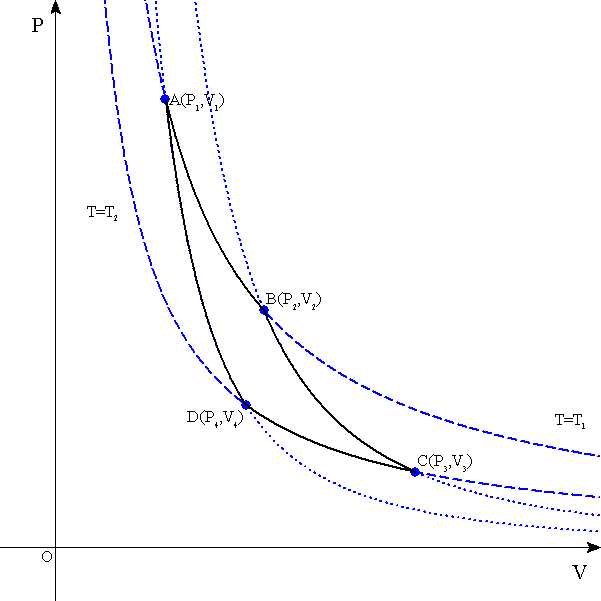
ボイル・シャルルの法則より、一定温度の理想気体の圧力と体積は、反比例する。したがって、縦軸に圧力P、横軸に体積VをとったP-Vグラフ上では、同じ温度を結んだ「等温線」は反比例のグラフ(直角双曲線)として表される。
状態方程式を見れば明らかなように、PVの積に比例して、Tも大きくなるから、「等温線」は座標軸から離れるほど、高温を表していることになる。
- 気体がする仕事
[J]=[N・m]=[(N/m2)・m3]=[Pa・m3]であるから、気体が外部に対してする仕事は、
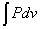
で表される。
dv>0すなわち「膨張」のとき、「正の仕事」
dv<0すなわち「圧縮」のとき、「負の仕事」
であり、これは、P-Vグラフ上の曲線下の面積で表される。
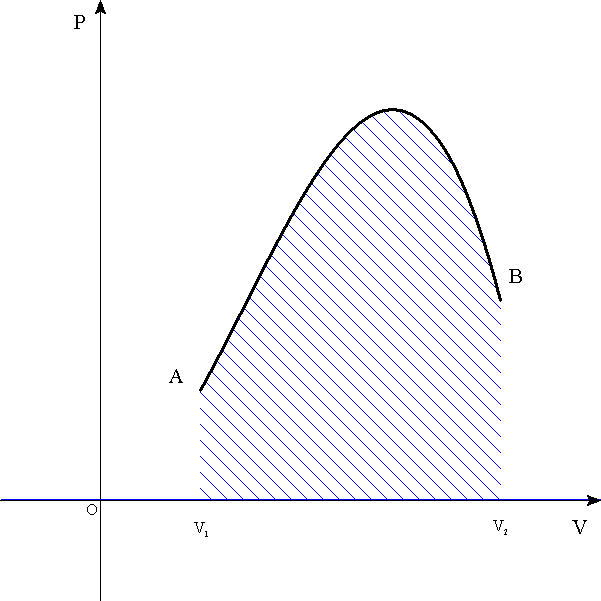
AからBへ(膨張)
BからAへ(圧縮)
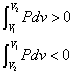
- もう一つの変数Tはどこに表されているか?
気体の状態を記述する変数は、圧力P[Pa=N/m2]、体積V[m3]、温度T[K]の3つである。それらの相互関係を明らかにしたのが、以下の法則である。
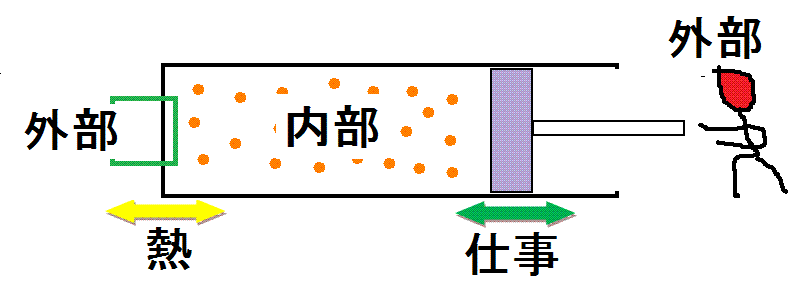
「熱力学第一法則」が考える「モデル」
- 完全な断熱材で出来た容器、摩擦が一切ないピストン、そこに閉じ込められた「理想気体」(分子間力・分子の大きさがない)。
- 容器に閉じ込められた「気体」を「内部」と呼び、「第一法則」では、これを主語として、「内部」の立場に立って、ものごとを考える。
- 吸熱:「内部」が、「外部(高温物体)」から、熱を受け取った。「外部」は、熱を失った。
- 放熱:「内部」が、「外部(低温物体)」に、熱を奪われた。「外部」は、熱を受け取った。
- 圧縮:「内部」が、「外部(ピストンを押す人)」から、仕事を受け取った。「外部」は、正の仕事をした。
- 膨張:「内部」が、「外部(ピストンを支える人)」を押し返し、仕事を与えた。「外部」は、負の仕事をした。
「内部」が「外部」から「受け取った」ものが「プラス」であり、「内部」が「外部」に「与えた」ものが「マイナス」である。 - 「外部」との「エネルギー」のやり取りをする「窓口」は、ただ二つだけ用意されている。
- ピストンの移動に伴って、「仕事」がやりとりされる。
- 熱交換器(「内部」の気体より「高温」または「低温」の物体との接触)によって、「熱」がやりとりされる。
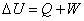
 U:内部エネルギーの増加量[J]
U:内部エネルギーの増加量[J]
言葉の定義上、「増加」したとき「プラス」、「減少」したとき「マイナス」の値をとる。
「内部エネルギー」は「絶対温度」のみの関数であり、「絶対温度」に比例するから、「増加」は「温度上昇」、「減少」は「温度下降」に対応する。
- Q:外部から受け取った熱[J]
「吸熱」・「熱を(外部から)受け取った」とき「プラス」、「放熱」・「熱を(外部に)与えた」とき「マイナス」。
- W:外部から受け取った仕事[J]
「圧縮」すなわち「外部」が「気体」に対して「正」の仕事をしたとき「プラス」、「膨張」すなわち「気体」が「外部」に対して「正」の仕事をしたとき、言いかえれば、「外部」が「気体」に対して「負」の仕事をしたとき、「マイナス」
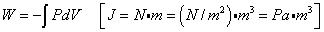
「気体」が「外部」から受け取る仕事は、上の式で表される。
マイナスがついているのは、「体積増加量」dVがプラスのときは、「気体」が「外部」に対して「正」の仕事をした、すなわち「膨張」に当たるからだ。
以上から、「熱力学第1法則」は、次のように「読む」ことができる。すなわち、
| 気体の「内部エネルギー」が増加したとすれば、その原因は、外部から「熱」を受け取ったか、もしくは、外部から「仕事」を受け取ったか、に限られる。 |
- 定積変化(dV=0すなわちW=0)
体積の変化がないから、気体は仕事をしない。従って、「熱力学第1法則」の式は以下のようになる。
 U=Q
U=Q
- 定圧変化
定圧変化では、「熱力学第1法則」の3項のうち、いずれも0とはならない。しかし、仕事Wは、圧力Pが体積Vにかかわらず一定であることから、積分記号の外に出すことができ、次のように書ける。
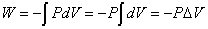
従って、「熱力学第1法則」の式は以下のようになる。
 U=Q-P
U=Q-P V
V
- 等温変化(
 T=0すなわち
T=0すなわち U=0)
U=0)
内部エネルギーは絶対温度のみの関数であり、従って「等温変化」においては、内部エネルギー増加量 Uはゼロである。
Uはゼロである。
従って、「熱力学第1法則」の式は以下のようになる。
0=Q+W
- 断熱変化(Q=0)
断熱変化においては、熱の出入りがないので、「熱力学第1法則」の式は以下のようになる。
 U=W
U=W
では、「断熱変化」のグラフはどんなグラフだろう?
「断熱膨張」をおこなったとしよう。「熱力学第1法則」の右辺はWのみであり、「膨張」においては「気体」が「外部」に「正」の仕事をしているから、「気体」は「外部」から「負」の仕事を受け取ったことになり、右辺は「負」である。
左辺は「内部エネルギー増加量」であるから、これが「負」であるなら、減少したことになる。内部エネルギーは絶対温度のみの関数であり、これに比例するから、温度が下がったことになる。すなわち、「断熱膨張により、温度は下がる」、まったく逆の推論をおこなえば、「断熱圧縮により、温度は上がる」
ボイルの法則で、Tが一定ならば、PとVは反比例の関係に立つ。縦軸P横軸VのP-Vグラフを描けば、直角双曲線となるが、一定値Tが大きくなればなるほど、つまり高温になるほど、この双曲線は座標軸から離れる。
「断熱膨張」においては、横軸V、体積増加とともに、温度が下降し、より座標軸に近い等温線に、乗り移る。
「断熱圧縮」においては、横軸V、体積減少とともに、温度が上昇し、より座標軸に遠い等温線に、乗り移る。
「断熱膨張により、温度は下がる」例 「断熱圧縮により、温度は上がる」例 - 低気圧にはまわりから空気が吹き込むから、内部では上昇気流が生じる。
- 海上で十分に水蒸気を含んだ空気塊が、急速に上昇する。
- 高度が高くなると、気圧が低いので、空気塊は急速に膨張する。
これはほぼ断熱過程とみなしうる。 - 温度が下がって、水蒸気が凝縮し、雨滴となる。
- 空気ポンプで自転車のタイヤに勢いよく空気を送り込む。
- 短い時間の間に圧縮するので、ほぼ断熱過程とみなしうる。
- チューブの先端の金具が熱くなるのは、空気の温度が上がったためである。
P-Vグラフから
- 温度が上がったか?、下がったか?→
 Uの正負がわかる。
Uの正負がわかる。
- 「外部」から仕事を受け取ったか?、「外部」に仕事をしたか?→Wの正負がわかる。
- その結果から、はじめて、Qの正負がわかる。
- ただし、断熱変化では、仕事の正負から、温度が上がったか?、下がったか?を判断しなければならない。
| 定積変化 | 定圧変化 |
| 過程 |  U U | = | Q | + | W | |
| A→B | 定積 | 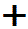 (温度上昇) (温度上昇) | = | 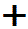 (吸熱) (吸熱) | + | 0 |
| B→A | 定積 | 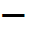 (温度下降) (温度下降) | = | 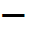 (放熱) (放熱) | + | 0 |
| A→C | 定圧 | 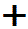 (温度上昇) (温度上昇) | = | 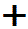 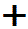 (吸熱) (吸熱) | + | 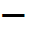 (膨張) (膨張) |
| C→A | 定圧 | 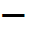 (温度下降) (温度下降) | = | 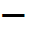 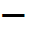 (放熱) (放熱) | + | 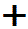 (圧縮) (圧縮) |
| 等温変化 | 断熱変化 |
| 過程 |  U U | = | Q | + | W | |
| B→C | 等温 | 0 | = | 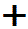 (吸熱) (吸熱) | + | 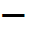 (膨張) (膨張) |
| C→B | 等温 | 0 | = | 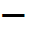 (放熱) (放熱) | + | 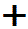 (圧縮) (圧縮) |
| B→D | 断熱 | 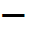 (温度下降) (温度下降) | = | 0 | + | 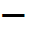 (膨張) (膨張) |
| D→B | 断熱 | 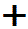 (温度上昇) (温度上昇) | = | 0 | + | 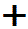 (圧縮) (圧縮) |
- P-Vグラフ上を、
- 「時計回り」に閉曲線を描くと、囲まれた部分の面積に当たる「仕事」が、「外部」に残されたことになる。
上側の「正」の面積から、下側の「負」の面積を引くことになるからだ。 - 「反時計回り」に閉曲線を描くと、囲まれた部分の面積に当たる「仕事」が、「内部」に残されたことになる。
上側の「負」の面積の方が、下側の「正」の面積より大きく、気体が「外部」にした仕事は合計で「負」となるからだ。
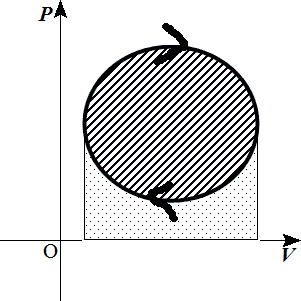
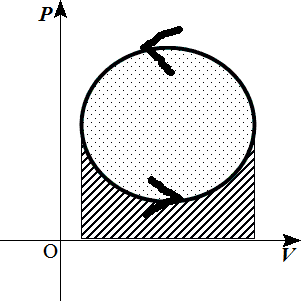
時計回り 反時計回り
- 「時計回り」に閉曲線を描くと、囲まれた部分の面積に当たる「仕事」が、「外部」に残されたことになる。
- 「時計回り」に回した場合、これは、「熱」を加えて「仕事」を取り出す、「熱機関」とみなすことができる。
- 「熱」(input)に対する「仕事」(output)の割合を、「効率」と呼ぶ。
- 「外部」に対してした「仕事」(output):「プラス」、「マイナス」とも考慮した、「正味」の値を用いる。
これは、P-Vグラフ上の閉曲線で囲まれた面積に当たる。 - 「外部」から受け取った「熱」(input):こちらは、「受け取った」を文字どおりに解釈して、「吸熱」のみを加算する。
まわりの空気を暖めて、「散逸」してしまった「熱」をふたたび集めて「仕事」に変換することは不可能だ(熱力学第二法則)という、「熱」というエネルギーの形態の、特殊性をあらわしている。
熱機関の「効率」e= 「熱機関」が「外部」へなした「正味の」「仕事」(プラスもマイナスも) 






「熱機関」が「外部」から受け取った「熱」(プラスのみ)
- 「外部」に対してした「仕事」(output):「プラス」、「マイナス」とも考慮した、「正味」の値を用いる。
- 熱機関の「効率」の計算例
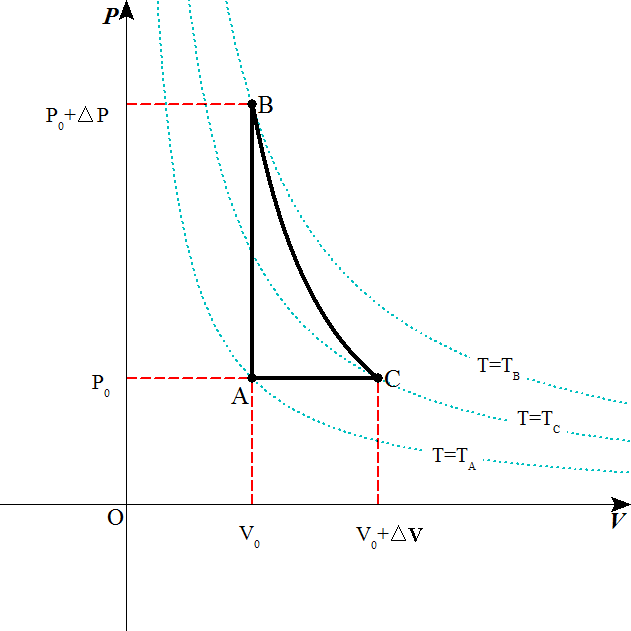
状態A,B,Cでの、状態方程式 - [A] P0V0=nRTA
- [B] (P0+
 P)V0=nRTB
P)V0=nRTB
- [C] P0(V0+
 V)=nRTC
V)=nRTC
→ 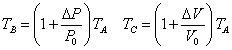
| 過程 |  U U | = | Q | + | W | |
| A→B | 定積 | 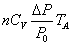 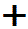 | = | 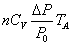 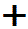 | 0 | |
| B→C | 断熱 | 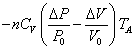 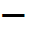 | = | 0 | + | 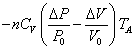  |
| C→D | 定圧 | 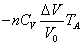 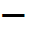 | = |  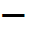 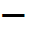 | + | 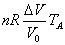 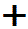 |
-
したがって、「効率」は、
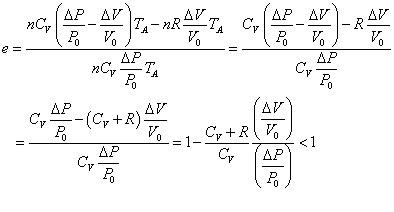
- 定積変化
QV=nCV定積変化  U
U= QV + 0  T
T
であるから、
 U=nCV
U=nCV T・・・(1)
T・・・(1)
すなわち、
U=nCVT :「内部エネルギー」は「絶対温度」のみの関数であり、これに比例する
「単原子分子理想気体」では、CV=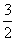 R
R
- 定圧変化
QP=nCP定圧変化  U
U= QP - P  V
V T
T
である。
また、状態方程式PV=nRTで、P一定だから、
P V=nR
V=nR T・・・(2)
T・・・(2)
したがって、
QP= U+P
U+P V
V
(1)(2)より、
QP=nCV T+nR
T+nR T=n(CV+R)
T=n(CV+R) T
T
- 以上から、
CP=CV+R
「単原子分子理想気体」では、CP=CV+R=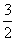 R+R==
R+R==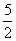 R
R
- 断熱膨張A→Bについて、熱力学第一法則を書くと、
過程  U
U= Q + W A→B nCv(TB-TA) = 0 - 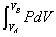
|
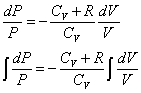
その解は、 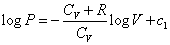 (ただし、c1は積分定数) (ただし、c1は積分定数)
すなわち、 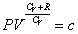
|
1辺の長さl[m]の立方体中にN[(個)]の単原子分子・理想気体の分子が入っているとする。分子同士の衝突は無視し、分子と壁面との衝突は、「完全弾性衝突」であるとする。
(「単原子分子」という仮定は、分子の回転にともなう運動エネルギーを無視するという意味である。)
|
x軸に垂直な壁面のみを考える
1回の衝突による1分子の運動量[kg・m/s]変化 |
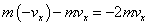
|
| 1回の衝突によって壁面が受ける力積[N・s] |
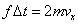
|
| 同じ分子が再び壁面に衝突するまでに要する時間[s] |
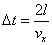
|
| 壁面がこの時間の間に平均的に受ける力[N] |
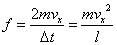
|
| この力をN個の分子について合算[N] |
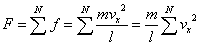
|
| N個の分子のx方向速度成分の「2乗平均」を用いて[N] |
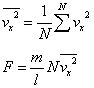
|
|
壁面の受ける圧力[Pa]
立方体の体積をV[m3]とすると |
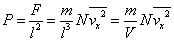
|
|
空間の「等方性」の仮定と
速度ベクトルの大きさの「2乗平均」 |
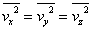
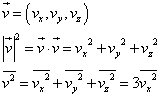
|
| これらを用いて、壁面の受ける圧力[Pa] |
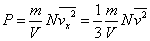
|
|
両辺にVをかけ、 気体分子の平均的運動エネルギーを用いて[J] |
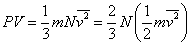
|
|
気体がn[mol]であったとすると、 アボガドロ数NAを用いて |
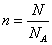
|
| 状態方程式と比較して、 |
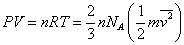
|
|
気体分子の平均運動エネルギーと絶対温度の関係[J] k=R/NA:ボルツマン定数 |
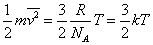
|
|
結論 気体の内部エネルギーは絶対温度のみの関数であり、 これに比例する |
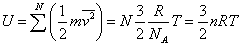
|
|
1[mol]についての内部エネルギーから、 定積モル比熱CV・定圧モル比熱CPを求めると[J/K・mol] |
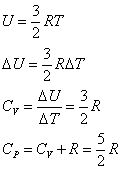
|
| 過程 |  U U | = | Q | + | W | |
| A→B | 等温 | 0 | = | nRT1log(V2/V1) | -nRT1log(V2/V1) | |
| B→C | 断熱 | -nCV(T1-T2) | = | 0 | + | nCV(T1-T2) |
| C→D | 等温 | 0 | = | -nRT2log(V3/V4) | + | nRT2log(V3/V4) |
| D→A | 断熱 | nCV(T1-T2) | = | 0 | -nCV(T1-T2) | |
- たとえば、等温膨張A→Bで、気体が外部にした仕事は、以下の式で計算できる。
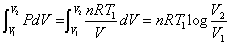
- この循環過程「カルノー・サイクル」の効率は、
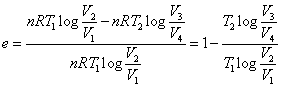
- ここで、以下の関係を用いると、(ただし、γ=CP/CV:「比熱比」とする)
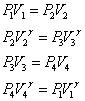
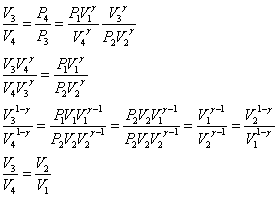
- したがって「カルノー・サイクル」の効率は
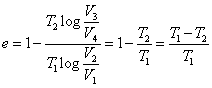
となり、- 高温物体の温度T1を限りなく高くするか、
- 低温物体の温度T2を限りなく絶対零度に近付けるか、
- 「熱機関」の効率を1にすること、つまり、「熱」をすべて「仕事」に変えることは、不可能であること、
- 絶対零度を実現することは不可能であること、
- 「熱」と「仕事」が、同じ単位ではかることのできる同質なものであることを示したのが、熱力学第一法則、であり、
- 「熱」は必ず高温物体から低温物体に向かって移動するしかない、という「熱」というエネルギーの特殊性を示したのが、熱力学第二法則、であると言える。