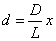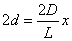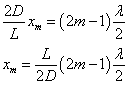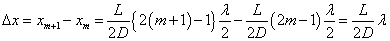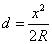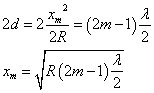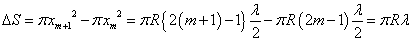「波」は、1点における振動が、まわりの空間を満たしている「媒質」によって、いくらかの時間的な「遅れ」をともなって、他の場所に「伝播」していく現象である。
座標原点において、y軸方向に質点が単振動を行っていたとする。「単振動」とは「等速円運動」の正射影であり、横軸に「時間」をとるとsinまたはcosの曲線で表すことができる。質点のまわりの空間は、空気・水などの媒質で満たされており、これらの媒質は「粘性」を持つから、質点の運動によってもたらされた媒質分子の元の位置からの「ずれ」が、隣接する媒質分子にも「ずれ」を引き起こし、原点での振動が、距離に比例した時間的な遅れをともなって、まわりの空間に伝えられていく。その空間的な広がりも、たとえばx軸方向の「ずれ」の分布もまた、sinまたはcosの曲線で表されることになる。
この「波動」という現象を記述する数式は、従って、xという空間的な「場所」を表す変数と、tという「時刻」を表す変数を含んでいる。
「時刻」tにおける、「場所」xでの、y軸方向の「変位」y(x,t)をxおよびtの関数として記述することが、ここでの目的である。
「場所」x=0(原点)において、質点が次の式で表される単振動を行っていたとする。
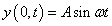
- A:振幅(y軸方向の変位が最大値または最小値を示すときの、原点からの隔たり[m])
- ω:「角速度」または「角振動数」(等速円運動の角速度[(rad)/s])
- T=2π/ω:「周期」(等速円運動をする点が1回転するのに要する時間[s])
と表される。
原点からx[m]だけ離れた場所には、この振動はどのように伝えられるだろうか?
波の「伝播速度」をv[m/s]とすれば、場所x[m]において時刻t[s]に生じている現象は、原点からそこに到達するのに(x/v)[s]かかっているから、原点においてすでにその(x/v)[s]前に起こった現象と同じはずである。
従って、
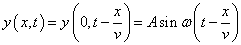
ここで、T=2π/ωの関係から、
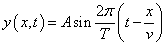
またここで、周期T[s]は、波が1波長分の長さだけ進行するのに必要な時間だから、
T=λ/v
この関係を用いて、
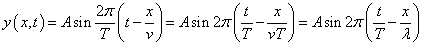
こうして波の「基本式」が得られた。右辺の最後の式の中括弧の中の第1項は、波を「時間」の関数としてとらえるとき、その『尺度』は周期Tであり、第2項は、波を「場所」の関数としてとらえるとき、その『尺度』は波長λであることを表している。
上の議論では、波がx軸の正方向に進行することを前提としていた。x軸の負の方向に進行する波の場合、場所x[m]において時刻t[s]に生じている現象は、原点には、そこに到達するのに(x/v)[s]かかるはずだから、原点においてその(x/v)[s]後に起こる現象と同じである。
従って、
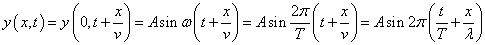
| 波の基本式 | |
| 右向き(x軸の正方向)進行波: | 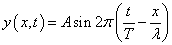 |
| 左向き(x軸の負方向)進行波: | 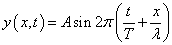 |
| |
これらの二つの波が、同時に発生したとき生じる現象について検討したい。その前に、「重ね合わせの原理」について述べる。
複数の波源で発生している波が、ある一つの場所に同時に到達したとき、その変位はそれぞれの波の持つ変位の、単なる算術的な加算によって表されることが知られている。これを「重ね合わせの原理」という。
この「原理」を拡張して考えると、時刻tにおける任意の「波形」が、次のようなシンプルな単振動の和として表現できることがわかる。
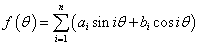
これを「フーリエ級数展開」と呼ぶが、これは時々刻々変化する波動のある特定の一瞬の「形」を、原理的には「無限個」であるが、近似的には「有限個」のan,bnの数値の「セット」として把握できることを意味する。 これが「デジタル」技術の根幹である。
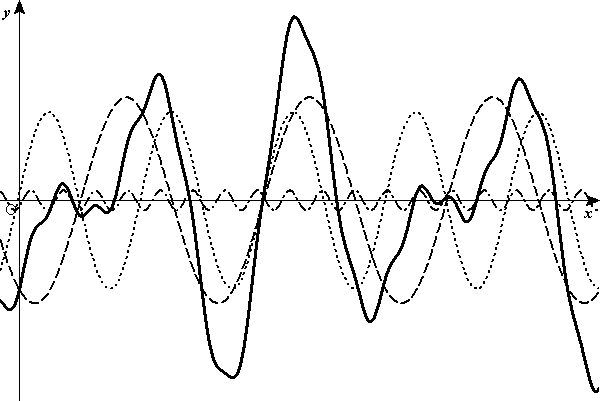
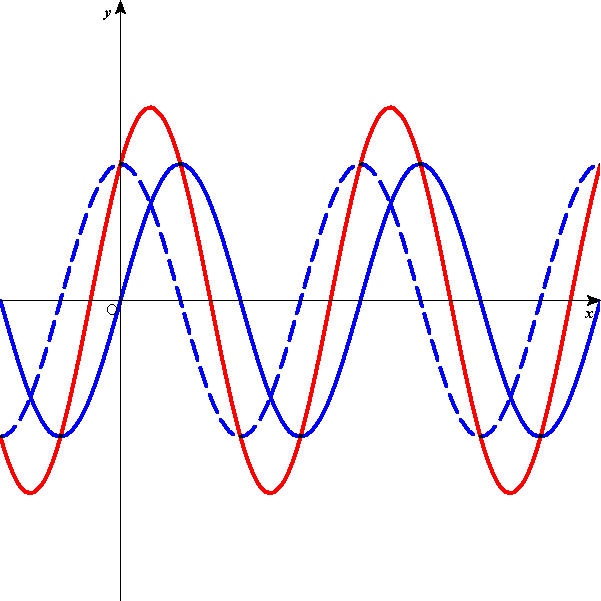
n=3程度でも、波長の異なる波を重ね合わせると、さまざまな形の波が得られる。2つほどサンプルを挙げる。図の中の破線、点線で表された3つの波を重ね合わせると、実線であらわされた波形になる。
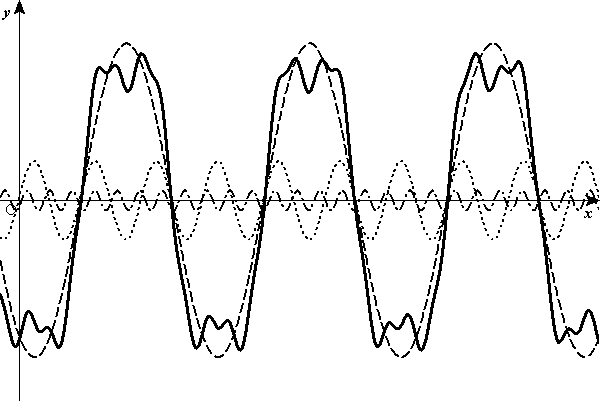 | 
|
三角関数の「加法定理」のうち、sinに関する2式
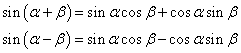
の両辺を加えると、
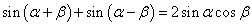
ここで、α+β=A,α-β=Bとおけば、α=(A+B)/2,β=(A-B)/2となるから、
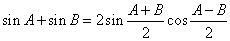
また、両辺の引き算を行うと、
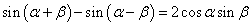
同様に、
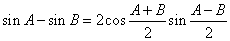
これらを用いて「定常波」の発生が説明できる。
振幅A、波長λ、伝播速度vの右向き進行波
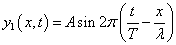
と、同じく振幅A、波長λ、伝播速度vの左向き進行波
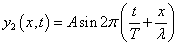
が、「重なり合う」と、
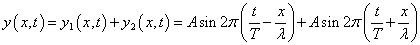
上の「和積の公式」を用いて、
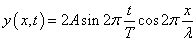
この式の特徴は、「時刻」に関する(t/T)の部分と、「場所」に関する(x/λ)の部分が、独立に、掛け算の形をとっていることにある。
「場所」を固定して考える。すなわち「場所」x=x0では、
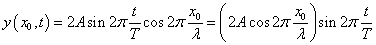
とかけるから、一定の振幅{2Acos2π(x0/λ)}で、単振動を行っていることがわかる。
「時刻」を固定して考える。すなわち「時刻」t=t0では、
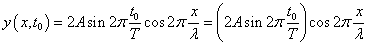
となり、この波は、時刻によってその最大値最小値は変えるものの、常に同じcosの「形」をした波、決して「進行」しない波を表していることがわかる。これが「定常波」であり、
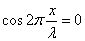
となる点、すなわち、任意の整数nに対して、
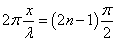 となる点が「節」であり、
となる点が「節」であり、
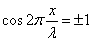
となる点、すなわち、任意の整数nに対して、
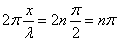 となる点が「腹」である。
となる点が「腹」である。
弦楽器の弦のように、振動する媒質の一端が「固定」されているものを「固定端」と呼び、ロープの一端を持って上下に振動させたときのように震動する媒質の一端が固定されていないものを「自由端」と呼ぶ。
進行する波が、性質の異なる媒質との境界面で「反射」を行う際、「固定端反射」、「自由端反射」と呼ばれる、2種類の異なった様式をとることが知られている。
- 「固定端反射」の条件
反射を行う端点において、入射波と反射波の合成波の振幅が0であること。入射波と反射波によって「定常波」が作られた場合、端点は「節」となる。
- 「自由端反射」の条件
反射を行う端点において、入射波と反射波の合成波の振幅が等しいこと。入射波と反射波によって「定常波」が作られた場合、端点は「腹」となる。
これらを数式によって確認する。
x軸上の定点x=lの地点に壁面があるとする。
この地点に、以下の式で表される「右向き」進行波が到達した。
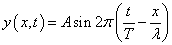
この波の壁面x=lにおける変位をy1とすると、

この壁面で発生する「反射波」の変位をy2とすると、
- 固定端反射の場合、
y1+y2=0であるから、
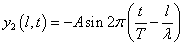
これを「波源」として、左向き(x軸方向負の向き)に進行する波を考える。
「場所」xにこの波は、(l-x)/v秒後に到達する。従って、反射波y'(x,t)は、
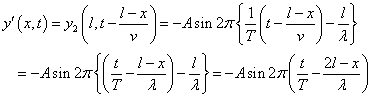
ここで、sin(π+θ)=-sinθであるから、
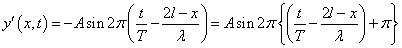
これをもって、「固定端反射」においては「位相がπずれる」といわれる。
固定端反射では、入射波と反射波は、点(l,0)に関して、点対象である。
合成波はY(x,t)=y(x,t)+y'(x,t)であらわされるから、
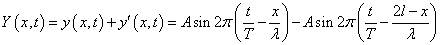
ここで、
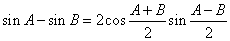
を用いて、
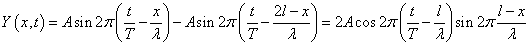
Y(l,t)=0であるから、反射点は「節」である。
- 自由端反射の場合、
y1=y2であるから、
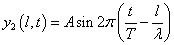
これを「波源」として、左向き(x軸方向負の向き)に進行する波を考える。
「場所」xにこの波は、(l-x)/v秒後に到達する。従って、反射波y'(x,t)は、
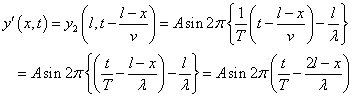
これをもって、「自由端反射」においては「位相がずれない」といわれる。
自由端反射では、入射波と反射波は、直線x=lに関して、軸対象である。
合成波はY(x,t)=y(x,t)+y'(x,t)であらわされるから、
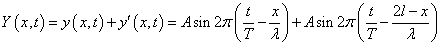
ここで、
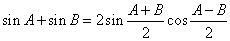
を用いて、
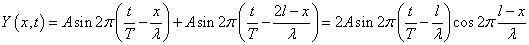
x=lにおいて、振幅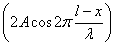 は最大値2Aをとるから、
反射点は「腹」である。
は最大値2Aをとるから、
反射点は「腹」である。
- 波の基本式、初期位相、振動速度分布、y-tグラフとy-tグラフ
上で、「波の基本式」を導いたが、これはいずれもsinの形を前提としていた。時刻t=0のとき、変位yが0であると決めていたからだ。もっと一般的に考えるために、時刻t=0のとき、変位yが0でない場合も含めて、「初期位相」という概念を導入する。
波の基本式 右向き(x軸の正方向)進行波: 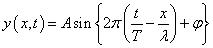
左向き(x軸の負方向)進行波: 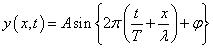
- y(x,t):場所x[m]、時刻t[s]におけるy方向の変位[m]
- A:振幅[m]
- T:周期[s]
- λ:波長[m]
- φ:初期位相[(rad)]
φにさまざまな値を代入することで、時刻t=0のとき、変位yが0でない場合も表現することができる。
次に、波はy軸方向のみを考えると「単振動」なのだが、その振動の速度vyが、波のそれぞれの場所で、どのような分布をとっているのかを調べたい。右向きの進行波について考える。
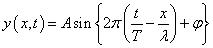
vyは、y方向の速度であるから、dy/dtである。
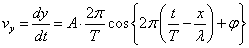
前にも述べたように、「波」という現象は、時刻tにおいて、xという場所で、どのような変位yをとるか?ということを問題にするため、どうしても「3次元」が必要になる。しかし、人間は、紙の上では、2次元しか認識できないから、「独立変数」t,xのいずれかを、「定数」に固定しなければグラフが描けない。
以下に、初期位相φとして、φ=0,φ=π/2,φ=π,φ=3π/2、という代表的な4つの場合について、- 時刻t=0のときの、y-xグラフ(これは「波形」を表す)
- 時刻t=0のときの、vy-xグラフ(これは、場所ごとの「振動速度分布」を表す)
- 場所x=0における、y-tグラフ(原点における「単振動」による、変位の時間的変化)
φ=0 y-xグラフ(t=0) 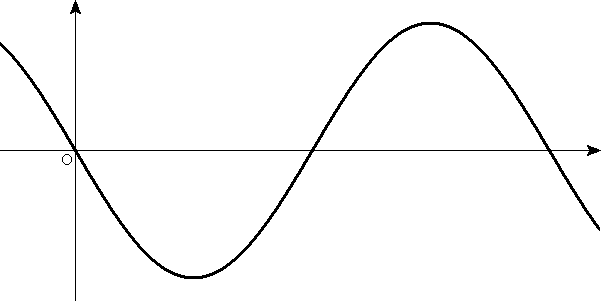
vy-xグラフ(t=0) 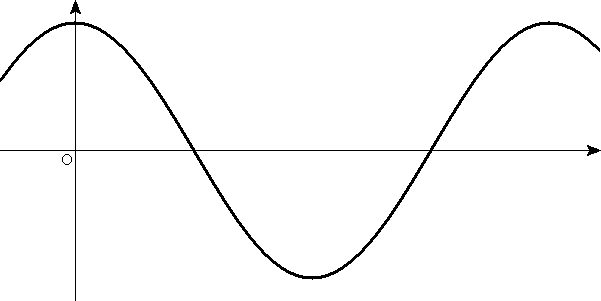
y-tグラフ(x=0) 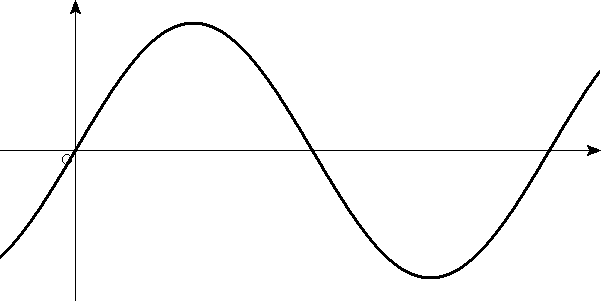
φ=π/2 y-xグラフ(t=0) 
vy-xグラフ(t=0) 
y-tグラフ(x=0) 
φ=π y-xグラフ(t=0) 
vy-xグラフ(t=0) 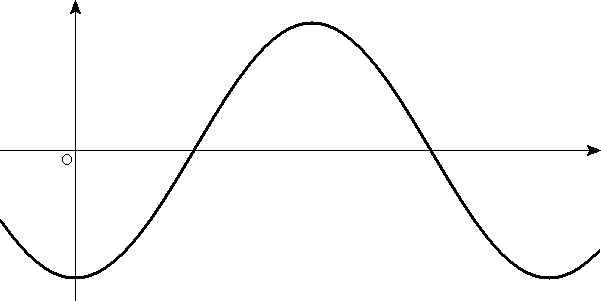
y-tグラフ(x=0) 
φ=3π/2 y-xグラフ(t=0) 
vy-xグラフ(t=0) 
y-tグラフ(x=0) 
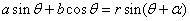
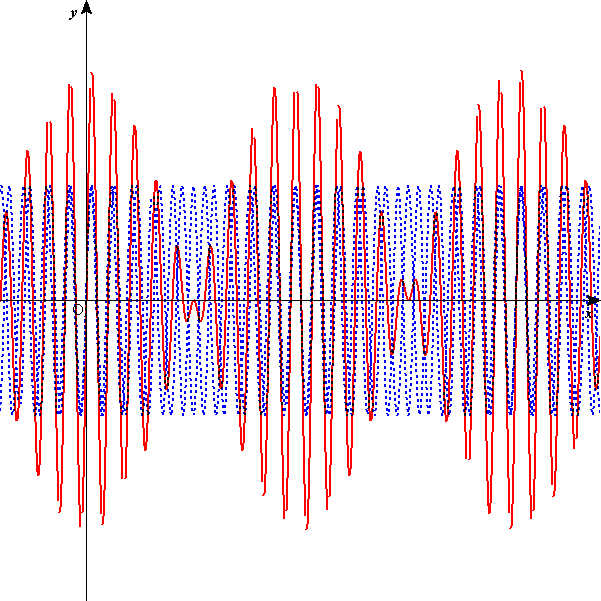
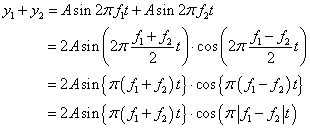
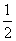 (f1+f2)、ということは、元の波とほとんど変わらないsin型の波と、
(f1+f2)、ということは、元の波とほとんど変わらないsin型の波と、
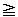 nλ (n=0,1,2,・・・)
nλ (n=0,1,2,・・・)
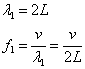
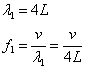
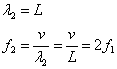

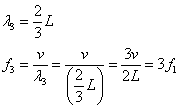
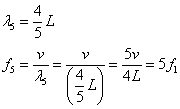
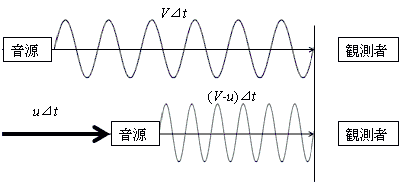
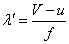 [m]
[m]
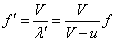 [Hz=1/s]
[Hz=1/s]
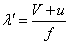 [m]
[m]
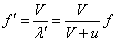 [Hz=1/s]
[Hz=1/s]
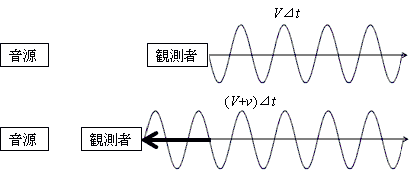
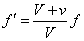 [Hz=1/s]
[Hz=1/s]
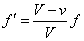 [Hz=1/s]
[Hz=1/s]
 短(高エネルギー)
短(高エネルギー)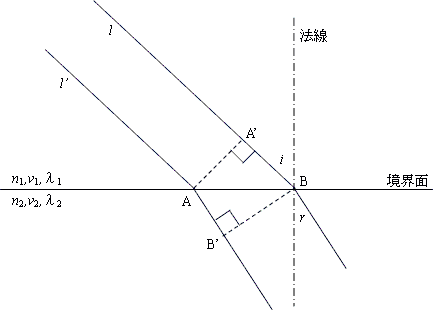
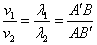
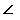 A'AB=i,
A'AB=i,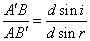
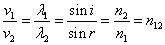
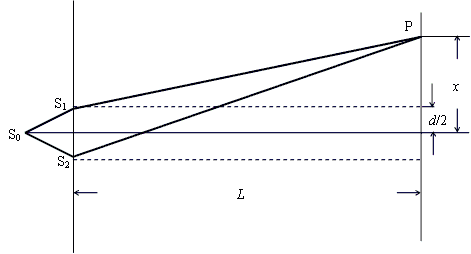
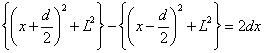
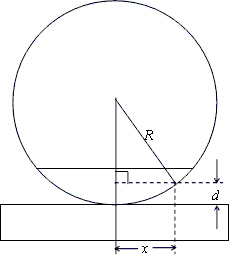
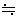 2Lと近似すると、
2Lと近似すると、
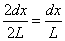
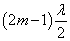 (m=1,2,3,・・・)
(m=1,2,3,・・・)
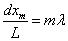
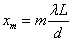
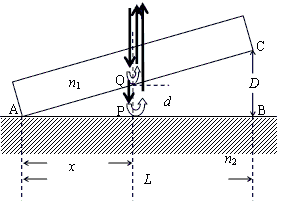
 xは、
xは、
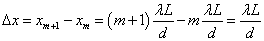
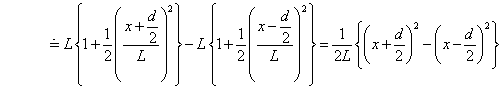
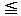 θ
θ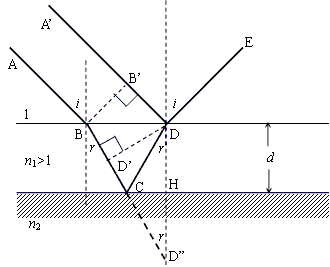
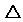 CHD
CHD