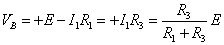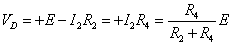- 力の「近接作用説」と「遠隔作用説」
- 近接作用説:力は、その物体と直接触れ合っているものからしか伝わるはずがない。
- 遠隔作用説:しかし、それでは、重力や静電気力はどうするのだ?これらの力は「真空」中でも伝わっているではないか?
- もし、「遠隔作用説」を否定するとすれば、重力や静電気力のもととなっているものから、まわりの空間に向かって「じわじわ」と「波動」のようなものが伝わっている、と仮定しなければならない。
- ただし、それは、通常考えられる「波」とも違うはずだ。振動すべき「媒質」がないのだから・・・。しかし、「波」の性質を備えた「光」は、真空中でも伝わるではないか?
- 今、この瞬間、太陽が消滅したとしよう。そのことによって、地球や地上の物体に作用する力は激変を受けるに違いないが、それは、一体、いつのことだ?
- 今、この瞬間、なのか?それとも、
- 「今、太陽が消滅した」という「情報」が、たとえば「光」の速度で地球に伝えられる、何年も後のことなのか?・・・
- 力学理論を「近接作用説」で統一しようとすれば、空気などの「媒質」のあるなしにかかわらず、その「作用」をじわじわと伝達させる「空間」自体の性質を問題にする必要が生じる。
そのような「空間」の性質が「場」と呼ばれる。- たとえば、「太陽」がそこにあることで、そこになかったときとは違った状態が、まわりの空間に生じている。これを「重力場」と呼ぼう。
- たとえば、「荷電粒子」がそこにあることで、そこになかったときとは違った状態が、まわりの空間に生じている。これを「電場」と呼ぼう。
- たとえば、「磁石」がそこにあることで、そこになかったときとは違った状態が、まわりの空間に生じている。これを「磁場」と呼ぼう。
「場」の中のどこかある場所に、なにか「試験体」になるものを、置いてみればよい。- 「重力場」のどこかに、質量m[kg]の物体を置いてみると、たしかにその物体に「力」[N](ベクトル量)が作用している!
だから、「そこ」は「重力場」である! - 「電場」のどこかに、
 1[C]の荷電粒子を置いてみると、たしかにその物体に「力」[N](ベクトル量)が作用している!
1[C]の荷電粒子を置いてみると、たしかにその物体に「力」[N](ベクトル量)が作用している!
だから、「そこ」は「電場」である! - 「磁場」のどこかに、1[wb]の磁石のN極を置いてみると、たしかにその物体に「力」[N](ベクトル量)が作用している!
だから、「そこ」は「磁場」である!
- 「電場」、「磁場」の定義
電場 磁場  1[C]の大きさのない荷電粒子(点電荷)を置いたとき、それにはたらく「力」(ベクトル量)をその場所における「電場」と呼ぶ。
1[C]の大きさのない荷電粒子(点電荷)を置いたとき、それにはたらく「力」(ベクトル量)をその場所における「電場」と呼ぶ。
- 「電場」もまた、(1)大きさと(2)方向をもつ「ベクトル量」である。
- 「電場」の大きさの単位は[N/C]である。
- 1[wb]の強さをもつ磁石のN極を置いたとき、それにはたらく「力」(ベクトル量)をその場所における「磁場」と呼ぶ。
- 「磁場」もまた、(1)大きさと(2)方向をもつ「ベクトル量」である。
- 「磁場」の大きさの単位は[N/wb]である。
- 「磁石」はどんなに小さく砕いても、その両端が必ずN極S極の対をなし、一方の極だけを取り出すことができない。
- 「重力場」についても、質量1[kg]の質点を置いたとき、それにはたらく「力」を「重力場」と呼ぶことにしてもよい。
1[c]あたりの力[N]だから、「電場」は[N/C]、1[wb]あたりの力[N]だから、「磁場」は[N/wb]、
そして、1[kg]あたりの力[N]だから、「重力場」の大きさは、[N/kg=m/s2]、つまり「重力加速度」だ!
- ここでも、まずたとえ話として「重力場」について考えてみよう。
- 地球表面近傍で観測される「重力」は、地球との「万有引力」であるから、地球の中心からr[m]離れた場所に置かれた質量m[kg]の物体には、
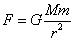 ・・・(1)
・・・(1)
という、距離の2乗の反比例した大きさの力が作用する。
したがって、地球の周りの「重力場」も、距離の2乗に反比例し、離れるに従って次第に弱まる「場」の形をもっている。 - ところが、地球の半径に比して、私たちが通常問題にする「長さ」は、余りにも小さいから、地球の中心から離れるに従って重力が小さくなる度合いは無視でき、
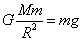
であらわされる一定の大きさの力が作用していると考えることができた。また、力の作用する方向も、すべて地球の中心に向かう方向であるから、これまた、私たちが問題にする狭い空間の中では、つねに同じ「下」の方を向いている、と考えてよかった。
だから、ここで考えている「重力場」は、同じ質量の物体に対しては、それをどこにおいても常に同じ大きさの力が同じ方向に作用する「一様」な「場」の形をとっている。
- 地球表面近傍で観測される「重力」は、地球との「万有引力」であるから、地球の中心からr[m]離れた場所に置かれた質量m[kg]の物体には、
- すべての「重力場」の在り方は、万有引力のもととなる複数の物体の広がりに応じて、(1)式を「足し算/積分」すれば得られるのだが、物事のもっとも単純な両極端として、上の二つ、すなわち、
- 距離の2乗に反比例し、離れるに従って次第に弱まる「場」
- どこにおいても常に同じ大きさの力が同じ方向に作用する「一様」な「場」
- 距離の2乗に反比例し、離れるに従って次第に弱まる「場」
・・・ 「1個の点電荷が作る電場」 - どこにおいても常に同じ大きさの力が同じ方向に作用する「一様」な「場」
・・・ 「コンデンサ内部の一様電場」
- 静電気力に関するクーロンの法則は、
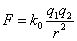
と、万有引力とまったく同じ形(逆二乗法則)をしている。
二つの電荷が同符号のとき「斥力」、異符号のとき「引力」という風に方向が逆転するところだけが、異なる。- したがって、「電場」の定義を適用すると、
「Q[C]の電荷をもつ、たった1個の点電荷しか存在しない空間」を考えたとき、その点電荷のまわりの空間には、 [N/C]の大きさをもつ、点電荷からの距離の二乗に反比例する「電場」が発生することになる。
[N/C]の大きさをもつ、点電荷からの距離の二乗に反比例する「電場」が発生することになる。
- その方向は、
- Qが正であるとき、点電荷から離れる方向、
- Qが負であるとき、点電荷に近付く方向、
- 空間内に二つ以上の電荷が存在するならば、そのまわりのある点における「電場」は、それぞれの電荷が作る「電場」を、ベクトル的に足し算することになる。
- したがって、「電場」の定義を適用すると、
- 金属板上に「無数」の「点電荷」が並んだコンデンサの極板のまわりの「電場」も、本来、このようにして、計算できるはずだ。
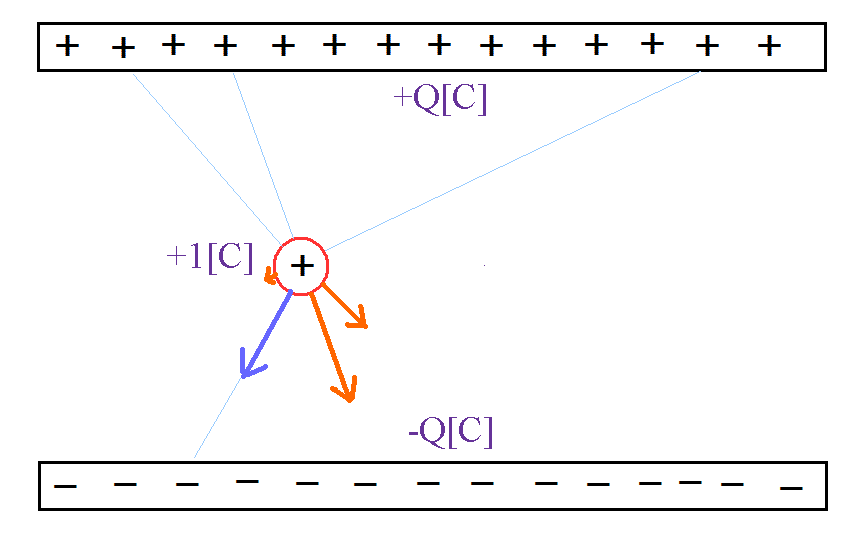
この簡単な絵からも、コンデンサ内部の「電場」が、(極板の端の方の影響を無視すれば)、- どこではかっても同じ大きさの、
- つねにプラスの極板から、マイナスの極板に向かう方向の、
その大きさを計算によって求めるには、かなり大変な「積分」を行わねばならないはずだが、それを避けるために「電気力線」というとても便利な考え方を用いる。
| とても単純な、二つの「電場」の形 | |
| 「1個の点電荷が作る電場」 | 「コンデンサ内部の一様電場」 |
|
|
U字型磁石の内部の空間などは、II型の「一様磁場」といえる。
- 「逆二乗法則」に従うものが自然界には大変多いのだが、それは何故だろう?
たとえば、点光源から発した光、煙突の先端から一定の速さで流れだす煙、・・・。
どこか一点から発した「もの」が、四方八方に「広がって」行くありさまを考えると、「遠ざかる」のにしたがって「弱まって」行くのは、それが通過するする面積が大きくなっているからではないか?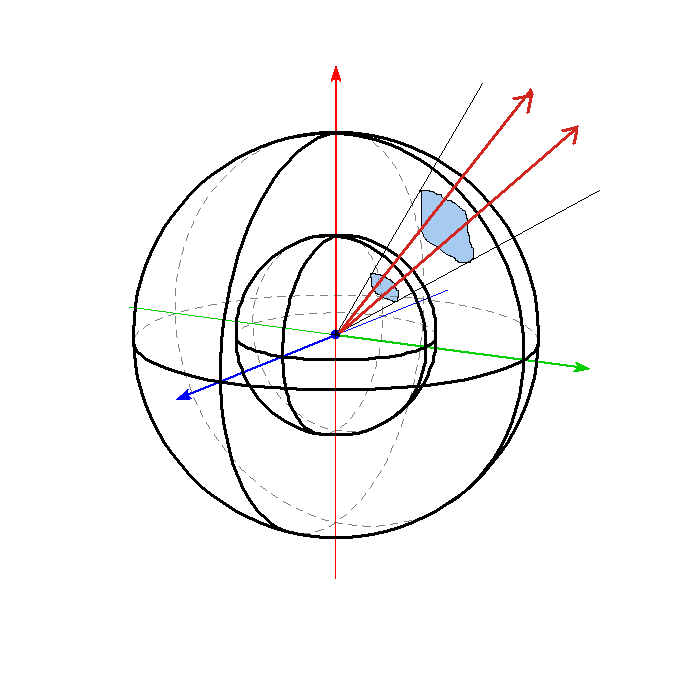
「源」となる一点を囲む「球」を考えてみよう。- 半径がa倍になれば、その表面積はa2倍になる。
- 「源」から一定の割合で出る「もの」を何本かの「矢印」で表したとすれば、その本数は、遠く離れても決して変わらない。
- 「源」からの距離がa倍になれば、「密度」はa2分の1に減る、
- こうして、一般に、
- 「湧き出し口」(source)から現れると、
- 「吸い込み口」(sink)に入るまで、
そして、いったん約束事を決めてしさえすれば、今度は、必ずしも「点」状の「源」でない「場」についても、この「流束」の考え方を押し広げて推測できるのだ。- 正電荷を「湧き出し口」(source)、負電荷を「吸い込み口」(sink)とするものが、「電気力線」、
- N極を「湧き出し口」(source)、S極を「吸い込み口」(sink)とするものが、「磁力線」、または、単位は異なるが、「磁束線」
- 「電気力線」についての約束事
- 「電気力線」などというものは、現実には存在していないのだから、それを何本引こうが、自由であろう。だから、「説明」が簡単になるように、「本数」を決めればよいが、一度決めればもちろん厳格に守らなければならない。
そこで、このように決められた。- 単位面積を垂直に横切る電気力線の本数が、
- その場所における「電場」の大きさをあらわすように決める。
そうすれば、もし、ある空間に「電気力線」を残らず描き込むことができたとしたら(!)
という大変便利なことになるはずだ。「電場」ベクトルの、 - 大きさは、単位面積を垂直に横切る電気力線の本数、
- 方向は、電気力線そのもの(正確にはその「接線」)の方向、
- 上の約束事からの帰結として、
となるのだが、これを確かめてみよう。 q[C]の点電荷から出る、「電気力線」の本数は、4πk0q(本)
q[C]の点電荷から出る、「電気力線」の本数は、4πk0q(本)
 q[C]の点電荷に入る、「電気力線」の本数は、4πk0q(本)
q[C]の点電荷に入る、「電気力線」の本数は、4πk0q(本)

 q[C]の点電荷を、点電荷の場所を中心とする半径r[m]の球面で囲む。
q[C]の点電荷を、点電荷の場所を中心とする半径r[m]の球面で囲む。
- 球の表面1[m2]を貫いて出てきた「電気力線」の本数が、その場、すなわち点電荷からr[m]離れた場所の「電場」の大きさを示していなければならないから、
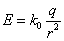
単位は本来、[N/C]であるが、これを、[(本)/m2]と読み替える。 - 1[m2]あたりで、
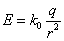 本、なのならば、「源」の点電荷から出たすべての「電気力線」本数を知るには、これに、球の表面積4πr2[m2]をかければよい。
本、なのならば、「源」の点電荷から出たすべての「電気力線」本数を知るには、これに、球の表面積4πr2[m2]をかければよい。
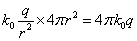
- 「電気力線」などというものは、現実には存在していないのだから、それを何本引こうが、自由であろう。だから、「説明」が簡単になるように、「本数」を決めればよいが、一度決めればもちろん厳格に守らなければならない。
- 上の約束事は「点電荷」についてのものだが、少し大雑把に、形や大きさのある「帯電体」についても適用できるとしよう。
 Q[C]に帯電した面積S[m2]の薄い金属板を考える。
Q[C]に帯電した面積S[m2]の薄い金属板を考える。
「薄い」というのは、厚さがないということ、つまり、側面からは「電気力線」が出ない(!)ということだ。
すると、この金属板からは、その上面と下面から、各2πk0Q本、合計4πk0Q本、の「電気力線」が出る。- 同様に、
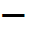 Q[C]に帯電した金属板には
Q[C]に帯電した金属板には
その上面へと下面へと、各2πk0Q本、合計4πk0Q本、の「電気力線」が入る。

- これら二枚の金属板を向い合せに、平行に、距離d[m]だけ隔てて並べよう。「電気力線」はどうなるだろうか?金属板を「越えて」延び続けるのだろうか?
- 帯電していない金属板の近くに正電荷を置けば、正電荷に面した側に「自由電子」が集められ、反対側には「自由電子」が不足した状態になるだろう。
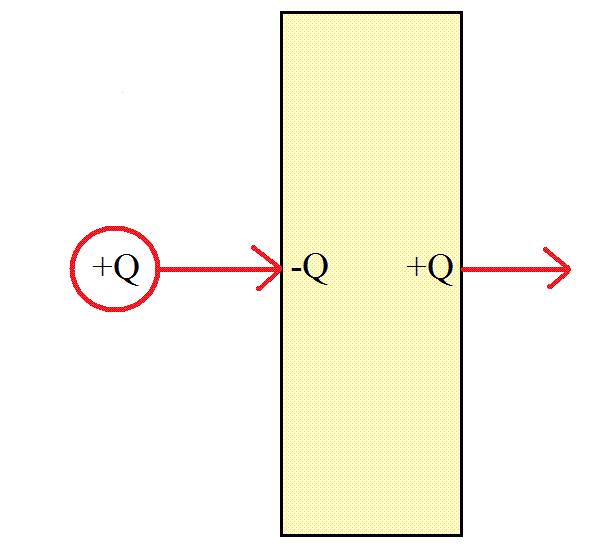
これはつまり、外部の正電荷(湧き出し口)から出た「電気力線」が一度は、金属板上の負電荷(吸い込み口)に入り、ふたたびちょうど反対側の正電荷(湧き出し口)から、出ていく、ことを意味している。
金属板自体が帯電していない、つまり、「自由電子」の負電荷と「原子核」の正電荷がつりあっている限り、入ってくる本数と、出ていく本数は、正確に同じである。
これを、「電気力線」が、通り抜けた、といってもよいだろう。 - こうして正に帯電した極板から出た「電気力線」は負に帯電した極板を通り抜けて延び続け(下図左実線)、
負に帯電した極板に入る「電気力線」も正に帯電した極板を通り抜けてその向こうからやってくる(下図左破線)ことになるはずだ。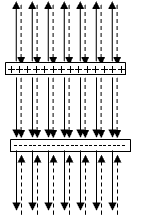
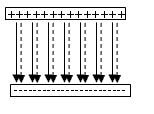
- 両極板の「外側」では、互いに反対を向いた「電気力線」が同数、並んでいる。「電気力線」密度が「電場」をあらわしていたことを考えれば、この空間ではベクトル量である「電場」が消えてしまった、ことになるだろう。
- 両極板の「内側」では、正の極板から負の極板へ向かう、同じ方向を向いた「電気力線」が並び、2πk0Q本と2πk0Q本、合計4πk0Q本、に重ね合わされている。
- 帯電していない金属板の近くに正電荷を置けば、正電荷に面した側に「自由電子」が集められ、反対側には「自由電子」が不足した状態になるだろう。
- こうして、コンデンサ内部の空間の「一様電場」が説明できた。
- どうして「一様」といえるのか?
- 金属板の中で、動くことのできる「電荷」は、「自由電子」のみである。
正に帯電、とは「自由電子」の不足状態、
正に帯電、とは「自由電子」の過剰状態、
のことである。
同符号の電荷は互いに反発し合うから、「自由電子」も、金属板上で等間隔に広がるはずだ。
だから、「電気力線」の出る場所も、入る場所も、やはり金属板上で等間隔に並んでいる。 - 「電気力線」は、金属板の表面から、その法線方向、つまり表面に垂直に、延びる。
物体の表面から何かが外に向かって放射されるときは必ずそうなのだが、これは、
もし、てんでバラバラの方向に延びるのだとしたら、局所的な不均等ができてしまうではないか(!)、と「背理法」的に納得することもできるだろう。
- 正の極板から負の極板に向かって、
- 極板に垂直に、
- 等間隔に、
その1[m2]当たりの本数はどこでも、同じ、すなわち、
「電場」ベクトルの、大きさも、方向も、つねに、一定、
である。 - 金属板の中で、動くことのできる「電荷」は、「自由電子」のみである。
- では、「電場」の大きさは?・・・単位面積を横切る「電気力線本数」であるから、
 [N/C]
[N/C]
- どうして「一様」といえるのか?
- その力のする仕事が、径路によらないものを「保存力」と呼ぶ。
【例1】 【例2】 - 上の図の【例1】の場合、質量mの物体が摩擦のない斜面の下まで滑り降りたとすると、
- 重力の斜面に垂直な成分は、垂直抗力とつりあっていて、この方向に物体は動かなかったから、これらは仕事をしない。
- 重力の斜面に平行な成分mgsinθのみが仕事をした。
斜面の下までの距離をlとすると、その仕事は、mglsinθ
lsinθ=hであるから、結局mgh
- 【例2】の場合はθの値が時々刻々変化するから、計算は複雑であろうが、
- 重力のその時々の斜面に垂直な成分、垂直抗力が仕事をしない。
- 重力のその時々の斜面に平行な成分のみが仕事をした。
という事情は同じであるから、その大きさはやはりmghになるだろう。
- 「保存力」に対しては、「位置エネルギー」を定義することができ、したがって、「エネルギー保存則」が成立する。
「エネルギー保存則」が成立するからこそ「保存力」なのだが、「エネルギー保存則」が成り立つような力が「保存力」なのだ、と定義してしまうと、「循環論法」になってしまう。-
「●●力」が作用する「場」において、「●●力」とちょうどつりあう外力によって、基準面から、質量m[kg]の質点を運んでくるときに必要な仕事を、「●●力」による「位置エネルギー」と呼ぶ。
- 上の図の【例1】の場合、質量mの物体が摩擦のない斜面の下まで滑り降りたとすると、
- 上に述べた「重力場」の二つの「形」に対応して、それぞれの「位置エネルギー(ポテンシャル)」を計算すると、
二つの「重力場」の「ポテンシャル」 万有引力 (地表面付近の)重力 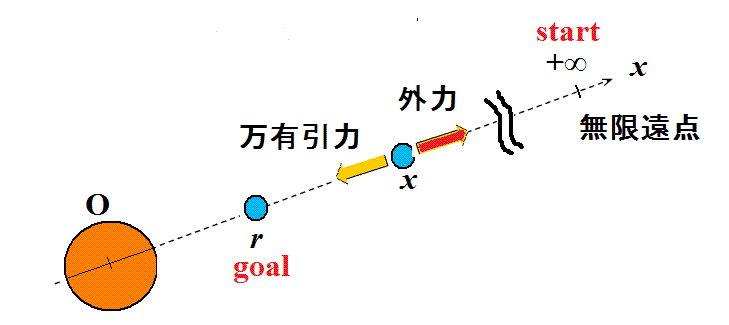
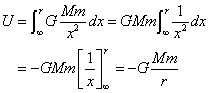


- 静電気力(クーロン力)もまた「保存力」であるから、同じように「位置エネルギー」を定義できる。
ただ、静電気力には重力と異なって「斥力」、「引力」の二種があり、これらをはっきりさせるためにも、
外力によって運ぶべき「もの」を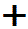 1[C]の点電荷(単位正電荷)に定め、
1[C]の点電荷(単位正電荷)に定め、
したがってその単位も、1[C]あたりの仕事[J]、すなわち[V=J/C]となっている。 - もちろん、「仕事」は「力」ベクトルと、「変位」ベクトルの「内積」であるから、大きさのみあって方向をもたないスカラー量であり、
したがって、1[C]あたりの仕事[J]である「電位」もまた、スカラー量である。 - 上に述べた代表的な二つの「電場」の形に対応して、それぞれの「電位」を計算してみる。
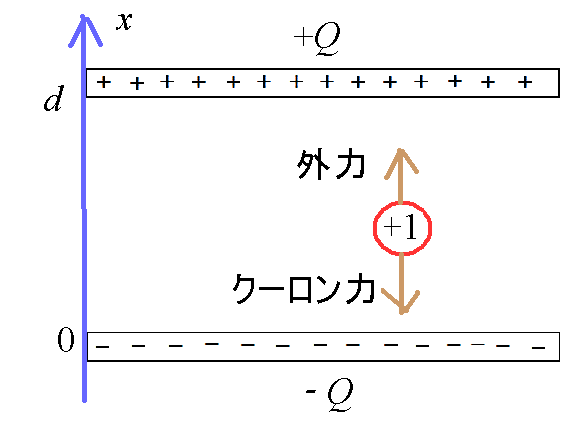
二つの「電場」における「電位」 一個の点電荷が作る「電場」 コンデンサ内部の「一様電場」 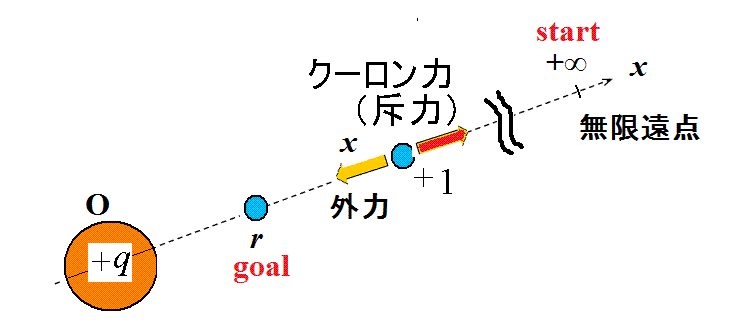
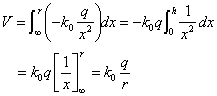
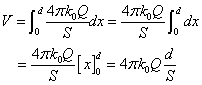
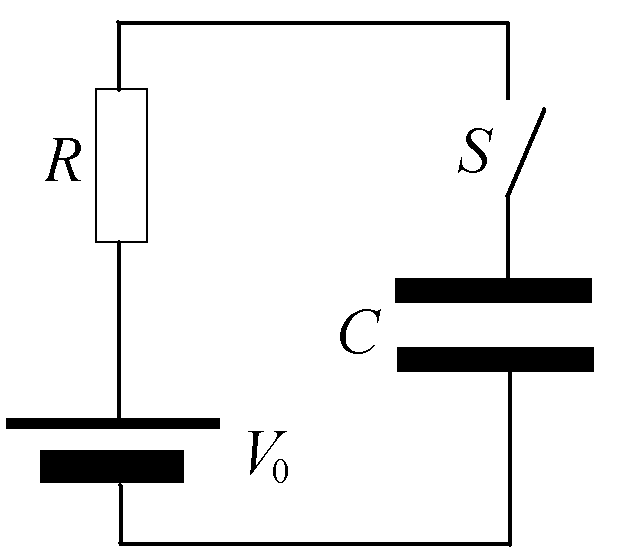
- コンデンサの基本的性質についての実験式
- 面積S[m2]の二枚の金属板を平行にd[m]だけ隔てて向かい合わせる。
- 起電力V0[V]の電池と抵抗R[Ω]とを、これと直列に接続し、スイッチを入れる。
- 電池の「負極」からは「自由電子」が流出し、同時に、電池の「正極」は「自由電子」を受け入れる。
この結果、- 下側の金属板は「自由電子」過剰、すなわち「負」に帯電、
- 上側の金属板は「自由電子」不足、すなわち「正」に帯電、
- 両極板間では、正電荷と負電荷が互いに引き合ったまま動けない状態だから、極板を挟む空間には、「電場」が生じ、極板間には「電位差」が生じる。
- その「電位差」が電池の起電力V0[V]より小さい間は、まだ電荷の移動が続くが、極板に蓄えられた正負の電荷の量が増えるほど「電位差」も大きくなり、いずれは、V0[V]と等しくなるだろう。
- そうなると、今度は抵抗Rの両端にかかる「電位差」が0[V]となってしまうから、電流の流れが止まる。
Q=CV
であり、この「比例係数」をコンデンサの「電気容量」と呼ぶ。 - 「電気容量」とは何か?
- 上の「電位」の計算例から、実は、もうわかっている。
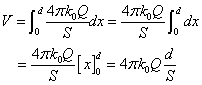
この式を書き直して、Qについて解くと、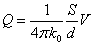
すなわち、「電気容量」Cとは、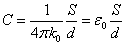
であった。 - 「電気容量」は、
- Sに比例して、
- dに反比例する、
- 同じ電位差に対してより多くの電荷を蓄えることのできるコンデンサが「優れた」コンデンサであろうから、この比例係数「電気容量」は、コンデンサの「能力」の指標である。
大きいほど「よい」コンデンサであるといえる。上の式から、「よい」コンデンサの条件は、- 金属板の面積Sが大きいこと、
- 向かい合わせた金属板の間隔dが小さいこと、
他にはないのだろうか?
- 上の「電位」の計算例から、実は、もうわかっている。
- 誘電体の挿入
- コンデンサの「電気容量」は、
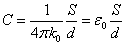
であるから、コンデンサの能力を高めるのに、- 金属板の面積Sを大きくすること、
- 向かい合わせた金属板の間隔dを小さくすること、
- 極板間の空間に、「誘電体(すなわち、不導体)」を充填することで、「誘電率ε」の値を大きくすることができる。
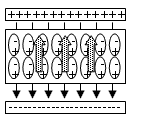
- 「不導体」であるからもちろん、自由電子はもたない。
しかし、分子結晶で出来た化合物を例にとると、どんな分子でもそれを構成する原子の「陰性(電子を引きつける性質)」に差があるから、分子内に多少の電荷の偏りを生じているものである(これを「極性」という)。 - また、固体では分子は結晶格子の間に閉じ込められていて、「自由に」動くことはできない。
- ただ、まわりの空間に強力な「電場」があれば、このように電荷の偏りのある分子は、結晶格子の定位置を中心に少し回転して位置をずらすことは考えられる。
- 周りに「電場」がないときには、分子はランダムにいろいろな方向を向いていたため、電荷の偏りにともなう微小な「電場」は打ち消されていた。
ところが、これが強力な「電場」の中で、一斉に向きを変えると(上図参照)、- 誘電体の上面、コンデンサの正の極板に近い側、には、負の電荷が、
- 誘電体の下面、コンデンサの負の極板に近い側、には、正の電荷が、
- コンデンサの作る外部の「電場」とは、逆向きの「電場」が、誘電体内部に形成されることになる。
- つまり、こうして、コンデンサの作る外部の「電場」は、誘電体内部の存在によって、弱められることになる。
- 「電場」が弱められると、どうして、コンデンサの能力が高まるのだ?
- 「電場」が弱まれば、極板間の「電位差」も小さくなる。
- より小さな「電位差」で、同じ量の電荷を蓄えることができるから、「よい」コンデンサなのである。
- 「誘電体」の物質ごとに決まる「誘電率」をε、その「誘電率ε」と「真空の誘電率ε0」との比を「比誘電率」εrという。
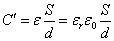
「比誘電率」εrはかならず1より大きい数値である。- 極板に蓄えられた電荷Q[C]に対して、極板間を横切る「電気力線本数」は、4πk0Q(本)すなわち、Q/ε0(本)
- したがって、極板間の空間の「電場」は大きさ
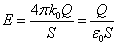 [N/C]
[N/C]
の「一様電場」、 - これが、「誘電体」の挿入によって、「誘電分極」のために逆向きの「電場」が形成され、
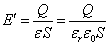 [N/C]
[N/C]
と、εr分の1に減少したのである。
- 「不導体」であるからもちろん、自由電子はもたない。
- コンデンサの「電気容量」は、
- コンデンサの蓄えるエネルギー(静電エネルギー)
- コンデンサは両極板に一定量の電荷を蓄えることができ、これをたとえば抵抗と接続すれば、熱や光を発生させることができるのだから、当然に、エネルギーをもっている筈だ。
- これは、次のように計算することができる。
- 電位の定義は、
「単位正電荷を、電場の力とちょうどつりあう外力で、基準面からその場所に、運ぶのに要する仕事」
すなわち、[V=J/C]であった。
エネルギーの単位[J]の様々な形 [ J = N・m = Pa・m3 = V・C ]
「力学」「熱力学」「電磁気学」 - つまり[J=V・C]、「エネルギー」を計算するには、
- 「電位差V」を「電荷Q」で積分する、または、
- 「電荷Q」を「電位差V」で積分する、
- ところでコンデンサに関しては、これら二つの量、「電荷Q」と「電位差V」の間には、
Q=CV
という関係が成り立つ。 - したがって、
- 「電位差V」を「電荷Q」で積分する
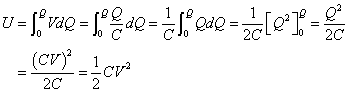
- 「電荷Q」を「電位差V」で積分する
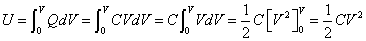
- 「電位差V」を「電荷Q」で積分する
- 電位の定義は、
- コンデンサの極板同士が、引く力
- コンデンサの二枚の金属板には、異符号の電荷が蓄えられているのだから、静電引力によって相互に引き合うことになる。
これをどのように計算すればよいだろうか? - クーロンの法則
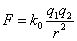
はあくまでも、たった二つの、しかも、大きさのない「点電荷」の間に作用する力についてしか教えてくれない。
極板上に並んだ「無数」の「点電荷」同士の膨大な数の組み合わせ(!)についての計算結果を加算すること、数学的にはそれは「積分」になるが、は、大変な作業なので、 - ここではいわば「どんぶり勘定」、
- その「力」に逆らって「微小な長さ」だけ極板を引き離したとき、「外力」がどれだけの仕事をするか?、
- 以下の手順で求める。
- コンデンサを電池につなぎ、充電する。
- スイッチを切った後、外力を加え、極板間隔を
 xだけ引き伸ばした。
xだけ引き伸ばした。
- スイッチを切るのは、電源からのエネルギー供給がないようにするためである。
- 本来極板間隔が変わればそれを引く力の大きさも変わるはずだ。ただし、微小な長さなので、その間は一定の力だとみなしうる、とする。
- はじめの状態の、コンデンサが蓄えるエネルギーUは、
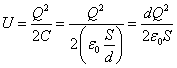
 xだけ引き伸ばした後の、コンデンサが蓄えるエネルギーU'は、
xだけ引き伸ばした後の、コンデンサが蓄えるエネルギーU'は、
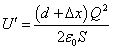
したがって、その差 U、外力が仕事を加えることによって増加したエネルギーは、
U、外力が仕事を加えることによって増加したエネルギーは、
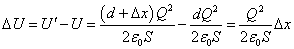
これが一定の外力外力Fがした仕事、F xに等しいとして、
xに等しいとして、
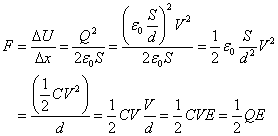
- コンデンサの二枚の金属板には、異符号の電荷が蓄えられているのだから、静電引力によって相互に引き合うことになる。
- 誘電体の挿入のエネルギー収支
- 【例題1】コンデンサを電池で充電したのち、スイッチを切ってから、極板間を比誘電率εrの誘電体でみたした。
誘電体を挿入するために、外力のした仕事を計算せよ。 - 【例題2】コンデンサを電池で充電したのち、スイッチをつないだまま、極板間を比誘電率εrの誘電体でみたした。
誘電体を挿入するために、外力のした仕事を計算せよ。
- 【例題1】
誘電体挿入前 誘電体挿入後 電荷Q[C] Q Q 電場E[N/C] 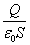
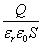
電位差V[V] 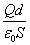
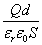
静電
エネルギー
U[J]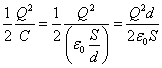
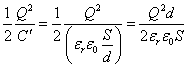
- 外力がした仕事をWとすると、U+W=U'であるから、

したがって、外力は「負の仕事」をしたことになる。つまり、誘電体は、近づけると自然に引きこまれる!
- 外力がした仕事をWとすると、U+W=U'であるから、
- 【例題2】
誘電体挿入前 誘電体挿入後 電位差V[V] V0 V0 電荷Q[C] 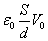
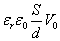
静電
エネルギー
U[J]
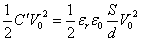
- ここでは、電池がした仕事(電池が供給したエネルギー)を考慮しなければならない
- [J=V・C]であるから、「エネルギー」を計算するには、
- 「電位差V」を「電荷Q」で積分する、または、
- 「電荷Q」を「電位差V」で積分する、
- ところで、電池というのは、つねに一定の「電位差」でエネルギーを供給する装置である。すなわち、V:一定、である。
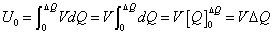
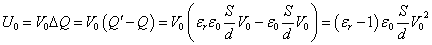
- [J=V・C]であるから、「エネルギー」を計算するには、
- 外力がした仕事W、電池が供給したエネルギーU0とすると、
U+W+U0=U'
であるから、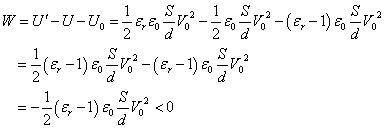
となり、やはり、外力は「負の仕事」をしたことになる。つまり、誘電体は、近づけると自然に引きこまれる!
- ここでは、電池がした仕事(電池が供給したエネルギー)を考慮しなければならない
- 【例題1】コンデンサを電池で充電したのち、スイッチを切ってから、極板間を比誘電率εrの誘電体でみたした。
- 複数のコンデンサの接続
- コンデンサの「電気容量」
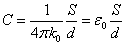
は、- 金属板の面積Sに比例し、
- 極板間隔dに反比例、
- 等しい面積S[m2]、極板間隔d[m]のコンデンサをn個用意する
- これを「並列」に接続すると、
- 極板間隔dは変わらず、
- 面積Sがn倍されたことになり、これに比例して、電気容量もn倍され、
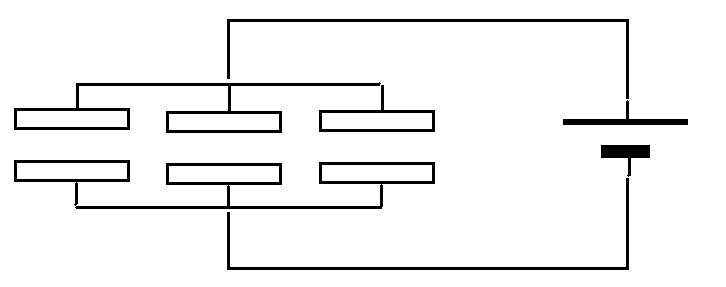
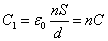
- これを「直列」に接続すると、
- 面積Sは変わらず、
- 極板間隔間隔dがn倍されたことになり、これに反比例して、電気容量もn分の1になる。
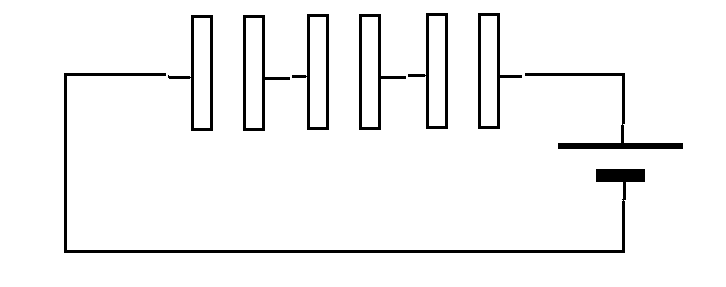
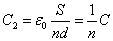
- また、ここから、コンデンサの極板間に、帯電していない薄い「導体」を挿入した場合についても類推できる。
- コンデンサの作る電場の内部におかれた「導体」、すなわち金属板には、「誘電体」の場合と異なって「自由電子」が存在するから、
- コンデンサの正極板に近い表面に、等しい量の負の電荷、
- コンデンサの負極板に近い表面に、等しい量の正の電荷、

- 「導体」表面の負の電荷に入り、
- 「導体」表面、反対側の正の電荷から、ふたたび等しい本数だけ、
「導体」表面にあらわれる電荷の量は、必ず、コンデンサの蓄える電荷の量に等しいから、「導体」内部では、- 外部の電場と大きさが等しい反対向きの電場があらわれ、
- これが、打ち消し合って、「導体」内部の電場がなくなった、
- コンデンサの作る電場の内部におかれた「導体」、すなわち金属板には、「誘電体」の場合と異なって「自由電子」が存在するから、
- これを「並列」に接続すると、
- 「並列」、「直列」の公式の導出
- 上で簡単に検討した、複数のコンデンサの「並列」接続、「直列」接続については、それらを一つのコンデンサで置き換えたとしたときに得られる電気容量、「合成容量」を求める公式があるが、これを導くには、
コンデンサ回路の計算の手順 - 未知数は
- 各コンデンサの蓄える電荷Q1,Q2,・・・Qn,
- 極板間の電位差V1,V2,・・・Vn,
- 各コンデンサについて、Q=CVが成立する・・・(条件式n個)
- 電荷保存の式
・・・電源と接続されていない、外部との「電荷」のやり取りがない、孤立した部分のうち独立なものについて - キルヒホッフ第2法則(閉回路を一周して各区間の「電位差」を加算すると、合計ゼロである)
・・・独立な閉回路について
・・・(3と4で合計、条件式n個)
- 未知数は
- 「並列」

- Q1=C1V1・・・(1)
Q2=C2V2・・・(2) - 電荷保存の式・・・(なし)
- キルヒホッフ第2法則
- 閉回路(V0-C1-V0)について : +V0-V1=0・・・(3)
- 閉回路(V0-C2-V0)について : +V0-V2=0・・・(4)
- 閉回路(C1-C2-C1)について : +V1-V2=0・・・これは(3)(4)に「従属」なので不要
- (3)(4)より、
V1=V0
V2=V0 - (1)(2)より、
Q1=C1V0
Q2=C2V0 - C1.C1を一つのコンデンサに置き換えると、
合計Q1+Q2の電荷が、電位差V0によって得られたから、合成容量Cは、
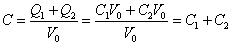
- 結論・・・面積が広がったとみなすことができ、「合成容量」は、いずれのコンデンサの単独の「容量」より大きい。
- Q1=C1V1・・・(1)
- 「直列」
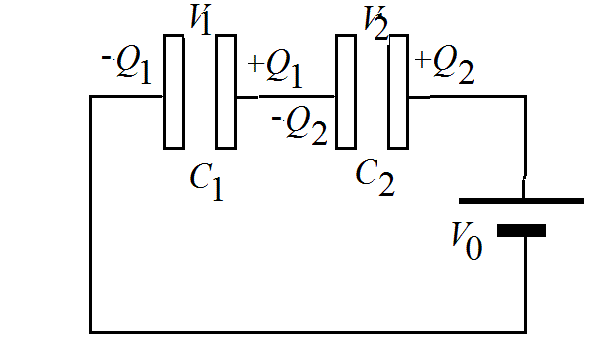
- Q1=C1V1・・・(1)
Q2=C2V2・・・(2) - 電荷保存の式
+Q1-Q2=0・・・(3) - キルヒホッフ第2法則(閉回路は一つしかない)
+V0-V1-V2=0・・・(4)
- (1)(2)(3)より、
C1V1=C2V2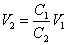
- (4)より、
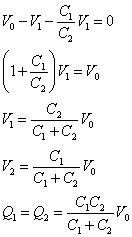
- C1.C1を一つのコンデンサに置き換えると、
全体でQ1=Q2の電荷が、電位差V0によって得られたから、合成容量Cは、
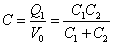
- 結論・・・極板間隔がが長くなったとみなすことができ、「合成容量」は、いずれのコンデンサの単独の「容量」より小さい。
- Q1=C1V1・・・(1)
- 上で簡単に検討した、複数のコンデンサの「並列」接続、「直列」接続については、それらを一つのコンデンサで置き換えたとしたときに得られる電気容量、「合成容量」を求める公式があるが、これを導くには、
- コンデンサの「電気容量」
- コンデンサのつなぎ換え
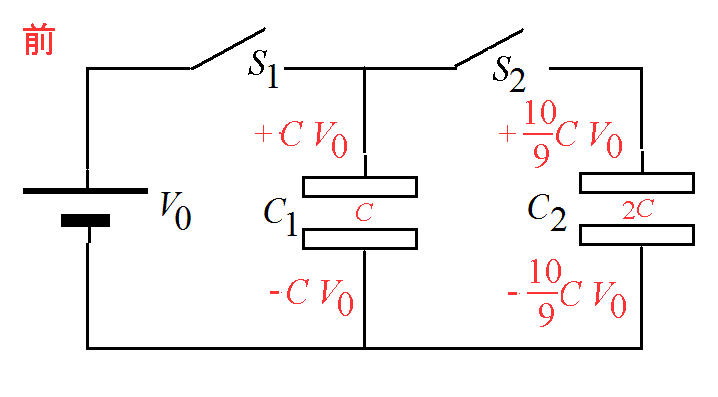
【例題】下図の回路でコンデンサC1の電気容量はC、C1の電気容量は2Cとする。- はじめいずれのコンデンサにも電荷は蓄えられておらず、スイッチも共に開いている。
- スイッチS1を閉じる。
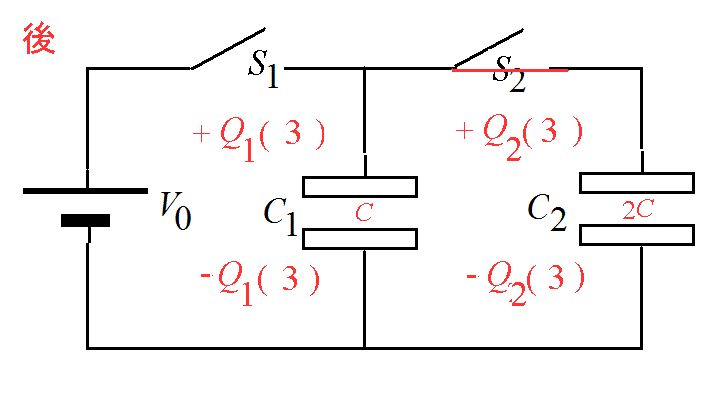
- 十分時間が経過したのち、S1を開き、続いてS2を閉じる。
- ふたたび十分時間が経過したのち、S2を開く。
- 以下、サイクルi〜iiiを繰り返す。
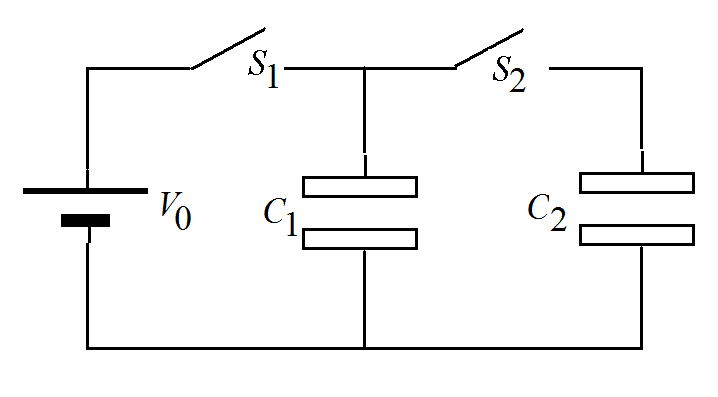
問- 一回目のサイクル終了後、
- コンデンサC1に蓄えられている電荷Q1(1)
- コンデンサC2に蓄えられている電荷Q2(1)
- 二回目のサイクル終了後、
- コンデンサC1に蓄えられている電荷Q1(2)
- コンデンサC2に蓄えられている電荷Q2(2)
- 三回目のサイクル終了後、
- コンデンサC1に蓄えられている電荷Q1(3)
- コンデンサC2に蓄えられている電荷Q2(3)
- n回目のサイクル終了後、
- コンデンサC1に蓄えられている電荷Q1(n)
- コンデンサC2に蓄えられている電荷Q2(n)
- このサイクルを無限に繰り返したとき、Q2(n)はどんな値に近づくか。
- 未知数は、Q1(1),Q2(1),V1(1),V2(1)
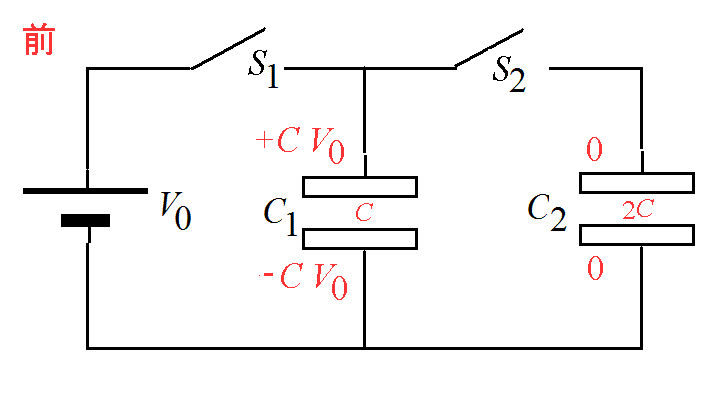

- Q1(1)=CV1(1)・・・(ア)
- Q2(1)=2CV2(1)・・・(イ)
- 電荷保存の式:+CV0+0=+Q1(1)+Q2(1)・・・(ウ)
- キルヒホッフ第2法則:+V1(1)-V2(1)=0・・・(エ)
(ア)(イ)(ウ)より:CV1(1)+2CV2(1)=CV0
すなわち、V1(1)+2V2(1)=V0
(エ)より:V1(1)=V2(1)=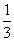 V0
V0
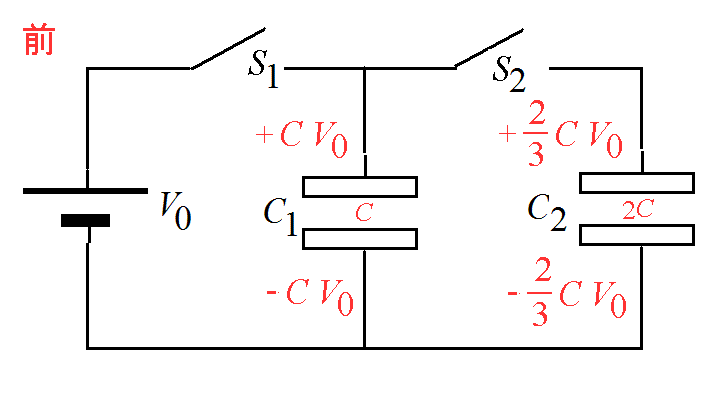
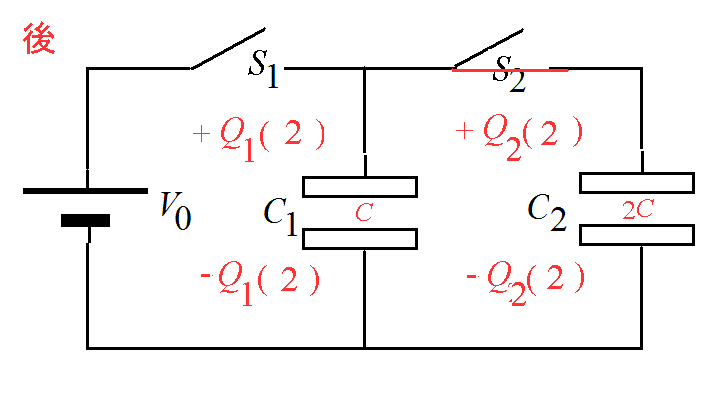
ふたたび(ア)(イ)より:Q1(1)=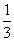 CV0 , Q2(1)=
CV0 , Q2(1)=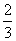 CV0
CV0
- 未知数は、Q1(2),Q2(2),V1(2),V2(2)
- Q1(2)=CV1(2)・・・(ア)
- Q2(2)=2CV2(2)・・・(イ)
- 電荷保存の式:+CV0+
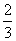 CV0=+Q1(2)+Q2(2)・・・(ウ)
CV0=+Q1(2)+Q2(2)・・・(ウ)
- キルヒホッフ第2法則:+V1(2)-V2(2)=0・・・(エ)
(ア)(イ)(ウ)より:CV1(2)+2CV2(2)=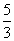 CV0
CV0
すなわち、V1(2)+2V2(2)=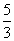 V0
V0
(エ)より:V1(2)=V2(2)=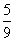 V0
V0
ふたたび(ア)(イ)より:Q1(2)=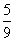 CV0 , Q2(2)=
CV0 , Q2(2)=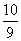 CV0
CV0
- 未知数は、Q1(3),Q2(3),V1(3),V2(3)
- Q1(3)=CV1(3)・・・(ア)
- Q2(3)=2CV2(3)・・・(イ)
- 電荷保存の式:+CV0+
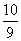 CV0=+Q1(3)+Q2(3)・・・(ウ)
CV0=+Q1(3)+Q2(3)・・・(ウ)
- キルヒホッフ第2法則:+V1(3)-V2(3)=0・・・(エ)
(ア)(イ)(ウ)より:CV1(3)+2CV2(3)=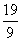 CV0
CV0
すなわち、V1(3)+2V2(3)=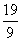 V0
V0
(エ)より:V1(3)=V2(3)=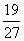 V0
V0
ふたたび(ア)(イ)より:Q1(3)=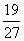 CV0 , Q2(3)=
CV0 , Q2(3)=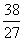 CV0
CV0
- 未知数は、Q1(n+1),Q2(n+1),V1(n+1),V2(n+1)
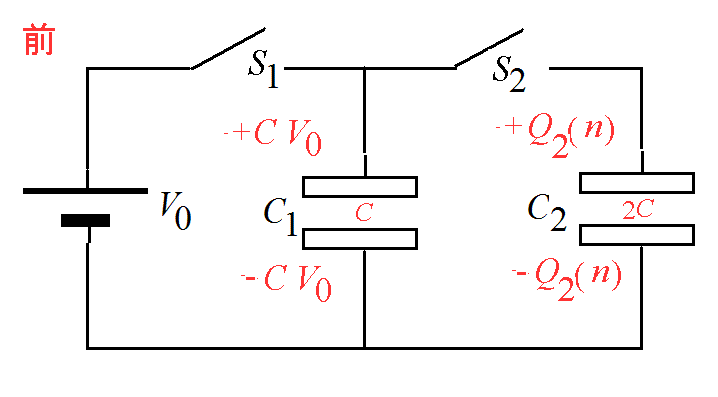
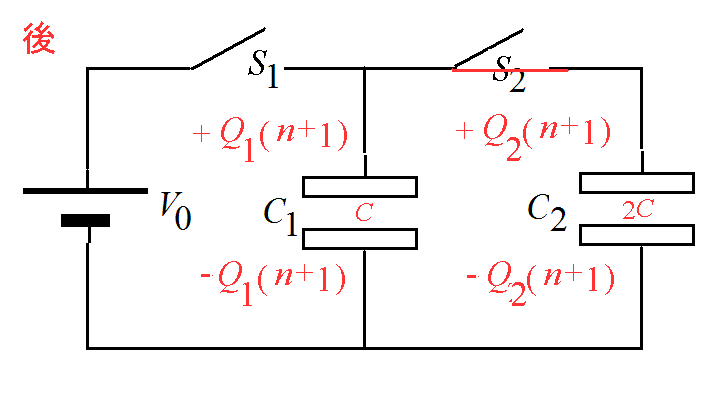
- Q1(n+1)=CV1(n+1)・・・(ア)
- Q2(n+1)=2CV2(n+1)・・・(イ)
- 電荷保存の式:+CV0+Q2(n)=+Q1(n+1)+Q2(n+1)・・・(ウ)
- キルヒホッフ第2法則:+V1(n+1)-V2(n+1)=0・・・(エ)
(ア)(イ)(ウ)より:CV1(n+1)+2CV2(n+1)=Q2(n)+CV0
すなわち、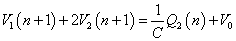
(エ)より: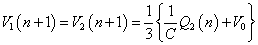
ふたたび(ア)(イ)より: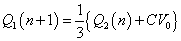 ,
, 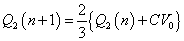
- では、こうして得られた「漸化式」を、解く。
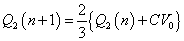 ・・・(オ)
・・・(オ)
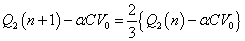 とおくと、
とおくと、
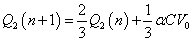 であるから、(オ)と比較して、α=2
であるから、(オ)と比較して、α=2
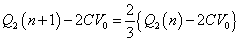
数列Q2(n)-2CV0は、初項:Q2(1)-2CV0、公比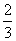 の等比数列である。
の等比数列である。

Q2(1)=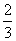 CV0であるから、
CV0であるから、
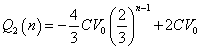 ・・・(カ)
・・・(カ)
- (カ)式で、nを無限大にすると、
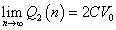
この「意味」を考えてみよう。- この回路では、各サイクルごとにiステップで、コンデンサC1は、電池によって満杯になるまで充電される。
- iiステップでは、このC1の満杯の電荷と、前サイクルでたまったC2の電荷の合計が、二つのコンデンサに、その容量に従って、1:2に分配される。
- こうしてC2の電荷も次第に増えていく。そして、C2もまた「満杯」になるまで、電荷の移動が続くだろう。
- とすると、「無限回」サイクル後というのは、もはやC2も満杯になってしまったことを意味する!
- 【参考】放電中と充電中のコンデンサの様子
- 放電中のコンデンサ
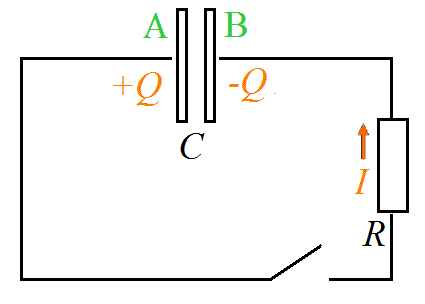
コンデンサのA極板に正電荷が蓄えられていたとすると、そこから「流れ出る」のが電流であるから、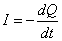
したがって、キルヒホッフ第2法則は、
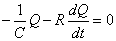

関数Qはその1階微分が元の関数に比例し、かつ符号が逆だから、Q0およびAという定数を用いて、
Q=Q0e-Atと仮定できる。両辺を微分して上の式に代入すると、定数Aが定まる。
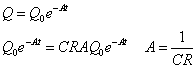
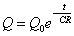
こうして関数Qの形が定まった。
スイッチを開いた瞬間の時刻をt=0とすると、このときコンデンサの電荷QはCV0だったとすると(初期条件)、これを上式に代入して定数Q0が定まる。
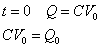
コンデンサに蓄えられた電荷の時間変化を示す式は、
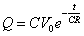
電流の時間変化を示す式は、
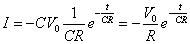
ここで電流の値が負になっているのは、コンデンサに電荷を蓄える方向に流れる電流を正としているからである。
電流の時間変化 電荷の時間変化
- 充電中のコンデンサ

電池の正極からコンデンサのA極板に向かう方向が電流の向きになるから、
したがって、キルヒホッフ第2法則は、
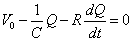
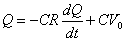
定数項CV0を消去するために、Q'=Q-CV0という「変数変換」を行うと、


関数Q'はその1階微分が元の関数に比例し、かつ符号が逆だから、Q0およびAという定数を用いて、
Q'=Q0e-Atと仮定できる。両辺を微分して上の式に代入すると、定数Aが定まる。
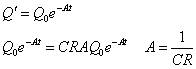
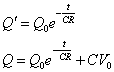
こうして関数Qの形が定まった。
スイッチを閉じた瞬間の時刻をt=0とすると、このときコンデンサの電荷Qは0だから(初期条件)、これを上式に代入すると、定数Q0が定まる。
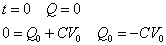
コンデンサに蓄えられた電荷の時間変化を示す式は、
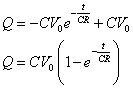
電流の時間変化を示す式は、
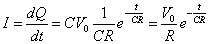
電流の時間変化 電荷の時間変化
- 放電中のコンデンサ
- 電流を「自由電子」の動きで説明する
- 電流は、電池の正極から出て、抵抗を通り、電池の負極に入る、と考えられている。
ところが、実際は(誰も見た者はいないが)、導線の内部を流れている「もの」は反対に、
電池の負極から出て、抵抗を通り、電池の正極に入る。
これが「電子」であって、その存在が確認される以前の時代に「電流の向き」の約束事が決められてしまっていたために、やむなく、負の電荷を持つ、ことになってしまった。 - 金属結晶の物質では、原子核の周りに強く拘束されている電子のほかに、最外殻にあって結晶内部を、「電場」による力を受けて移動できる電子があり、これを「自由電子」と呼ぶ。
「電流」とは、この「自由電子」の移動に伴う電荷の移動[A=C/s]にほかならない。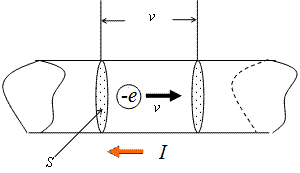
- 一般に流体の「速度」は、単位時間にある断面を通過する「もの」の量、で定義される。
- 上の図で「電流」は右から左に、したがって、「自由電子」左から右に移動しているものとする。
「自由電子」1個のもつ電荷(電気素量)はe[C]、その(平均的な)速度をv[m/s]とする。 - ここで、右側の断面を今から1秒以内に通過する電子は、すべて、その断面後方の底面積S[m2]、高さv[m]の円柱形に存在しているはずだ!
それらのもっている電荷[C]を合計すれば、これが「単位時間にある断面を通過する電荷量[C/S]」すなわち、「電流」Iである。 - この導体の電子密度(単位体積中に存在する「自由電子」の個数、金属の種類によって異なるであろう)をn[1/m3]とすれば、
I=enSv [C×(1/m3)×m2×(m/s)=C/s=A]
- 上の図で「電流」は右から左に、したがって、「自由電子」左から右に移動しているものとする。
- 電流は、電池の正極から出て、抵抗を通り、電池の負極に入る、と考えられている。
- 「抵抗」を「自由電子」の動きで説明する
- V[V]の電位差をかけられた「抵抗」の長さl[m]区間には、
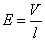 [V/m=N/C]の「一様電場」が生じている、と考えられる。
[V/m=N/C]の「一様電場」が生じている、と考えられる。
- 「抵抗」の内部の「自由電子」には、この「電場」によって高電位、すなわち電池の正極に近い側に向かって、引力を受ける。その大きさは、
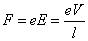 [N]
[N]
この力のみを受けているのならば、「自由電子」は加速度を持ち、抵抗線が長くなればなるほど大きな速度を持つことになるはずであるが、そのようなことは起こっていないようである。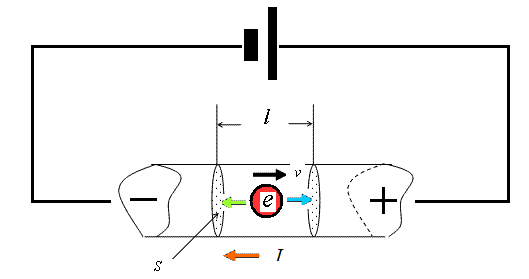
- 「抵抗」内部の金属結晶の様子を想像してみると、当然そこがなにもない空間ではなく、正の電荷をもつ金属原子の原子核が整然と並んでいるはずである。「自由電子」は、それらの原子核から引力を受けるのだが、「前方」にある原子核からは加速され、「後方」にある原子核からは減速され、・・・、といった複雑な動きをすることになるだろう。
これらの力を大雑把に「合算」して、ちょうど、自由落下する雨粒が空気抵抗によって、「終端速度」に達するように、ここでも、「自由電子」の速度v[m/s]に比例した抵抗力を受ける、と仮定してみよう。つりあいの式は、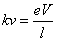
- ここに、上で求めた、電流の式、
I=enSv [C×(1/m3)×m2×(m/s)=C/s=A]
をもちいて、「自由電子」の速度v[m/s]を消去すると、
こうして、電流が電位差に比例する、という「オームの法則」が導かれて(!)しまったわけだ。すなわち、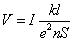
したがって、「抵抗」Rとは、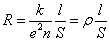
もちろん、こんな怪しげなモデルでは確定的なことは言えないが、少なくとも、「抵抗」は、- 長さに比例し、
- 断面積に反比例する、
- さらにここから、
- 抵抗の「直列接続」は、「長さ」が長くなる、と考えれば、より抵抗は大きくなり、
R=R1+R1 - 抵抗の「並列接続」は、「面積」が大きくなる、と考えれば、より抵抗は小さくなる、
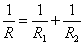
- 抵抗の「直列接続」は、「長さ」が長くなる、と考えれば、より抵抗は大きくなり、
- V[V]の電位差をかけられた「抵抗」の長さl[m]区間には、
- 抵抗の消費するエネルギー(ジュール熱)
エネルギーの単位[J]の様々な形 [ J = N・m = Pa・m3 = V・C ]
「力学」「熱力学」「電磁気学」- 「電力」Pは、
P=VI[W=V・A=(J/C)・(C/S)=J/S]
である。単位をみれば明らかなように、これは単位時間当たりのエネルギー、すなわち、「仕事率」であるから、 - 「抵抗の消費するエネルギー(ジュール熱)」Wは、「電力」を時間で積分したもの、になる。

- 「電力」Pは、
- 直流回路の計算
直流回路の計算の手順 - 未知数は
- 各抵抗を流れる電流I1,I2,・・・In,
- 各抵抗の両端の電位差V1,V2,・・・Vn,
- 各抵抗について、「オームの法則」V=IRが成立する・・・(条件式n個)
- キルヒホッフ第1法則
・・・回路が枝分かれしているポイントのうちのうち独立なものについて
各ポイントに単位時間「流入」する電荷と、そこから単位時間に「流出」する電荷の合計が0である、というのだから、これは、「電荷保存の式」といっていい。 - キルヒホッフ第2法則(閉回路を一周して各区間の「電位差」を加算すると、合計ゼロである)
・・・独立な閉回路について
・・・(3と4で合計、条件式n個)
【例題1】次の回路の各抵抗を流れる電流求めよ。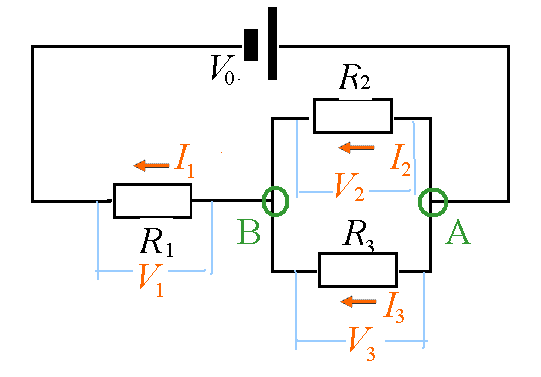
- 「オームの法則」
- V1=I1R1・・・(ア)
- V2=I2R2・・・(イ)
- V3=I3R3・・・(ウ)
- キルヒホッフ第1法則
- (図中「A」点について): +I1-I2-I3=0・・・(エ)
- (図中「B」点について): +I2+I3-I1=0・・・(エ)に「従属」だから、不要
- キルヒホッフ第2法則
- (回路V0―R2―R1―V0)について: +V0-V2-V1=0・・・(オ)
- (回路V0―R3―R1―V0)について: +V0-V3-V1=0・・・(カ)
- (回路R2―R3―R2)について: +V2-V3=0・・・(オ)(カ)に「従属」だから、不要
- (オ)(カ)からV2=V3
- (イ)(ウ)から
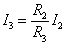
- (エ)から
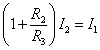
したがって、 ,
, 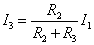
- ふたたび、(ア)(オ)から、
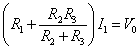
したがって、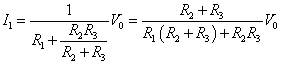
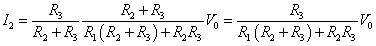
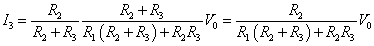
【例題2】「ホイットストーン・ブリッジ」
- 上の図で、R2 , R3は既知の抵抗、R4は可変抵抗である。
- R4を適宜操作することによって、検流計「G」に電流が流れないようにする。
- このときのR4の値から、未知の抵抗R1を知ることができる。
- 「検流計」に電流が流れないことが条件である。
B―Dに電流が流れないのは、その間に「電位差」がないからであり、ということは、その部分の導線を除去してしまっても同じだ!
結局、- E―P―A―B―C―P―E
- E―P―A―D―C―P―E
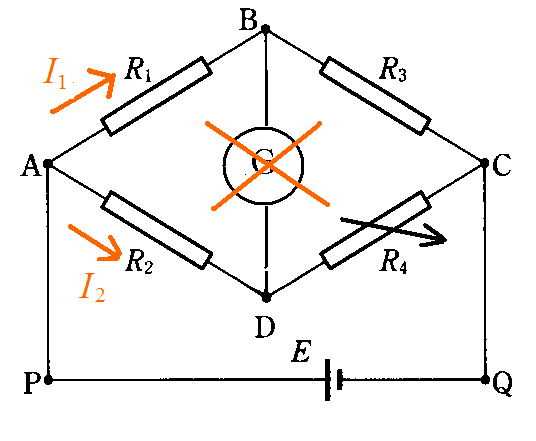
未知数I1 , I2 とする。
式の数を減らすために、オームの法則は、キルヒホッフ第2法則の式に組み込んでしまうことにする。
また、P―Q間に抵抗がないので、電池Eを通る電流を未知数としない。だから、キルヒホッフ第1法則も、なし。- キルヒホッフ第2法則
- (回路E―P―A―B―C―P―E) : +E-I1R1-I1R3=0・・・(ア)
- (回路E―P―A―D―C―P―E) : +E-I2R2-I2R4=0・・・(イ)
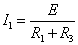 ,
, 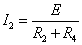
- 電池の負極を基準として、B点の電位VB , D点の電位VDを求める。
これらが等しいことから、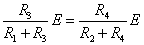
R3(R2+R4)=R4(R1+R3)
R3R2=R4R1
R1 : R3=R2 : R4
こうして、未知の抵抗R1を知ることができた。
【例題3】「非オーム抵抗」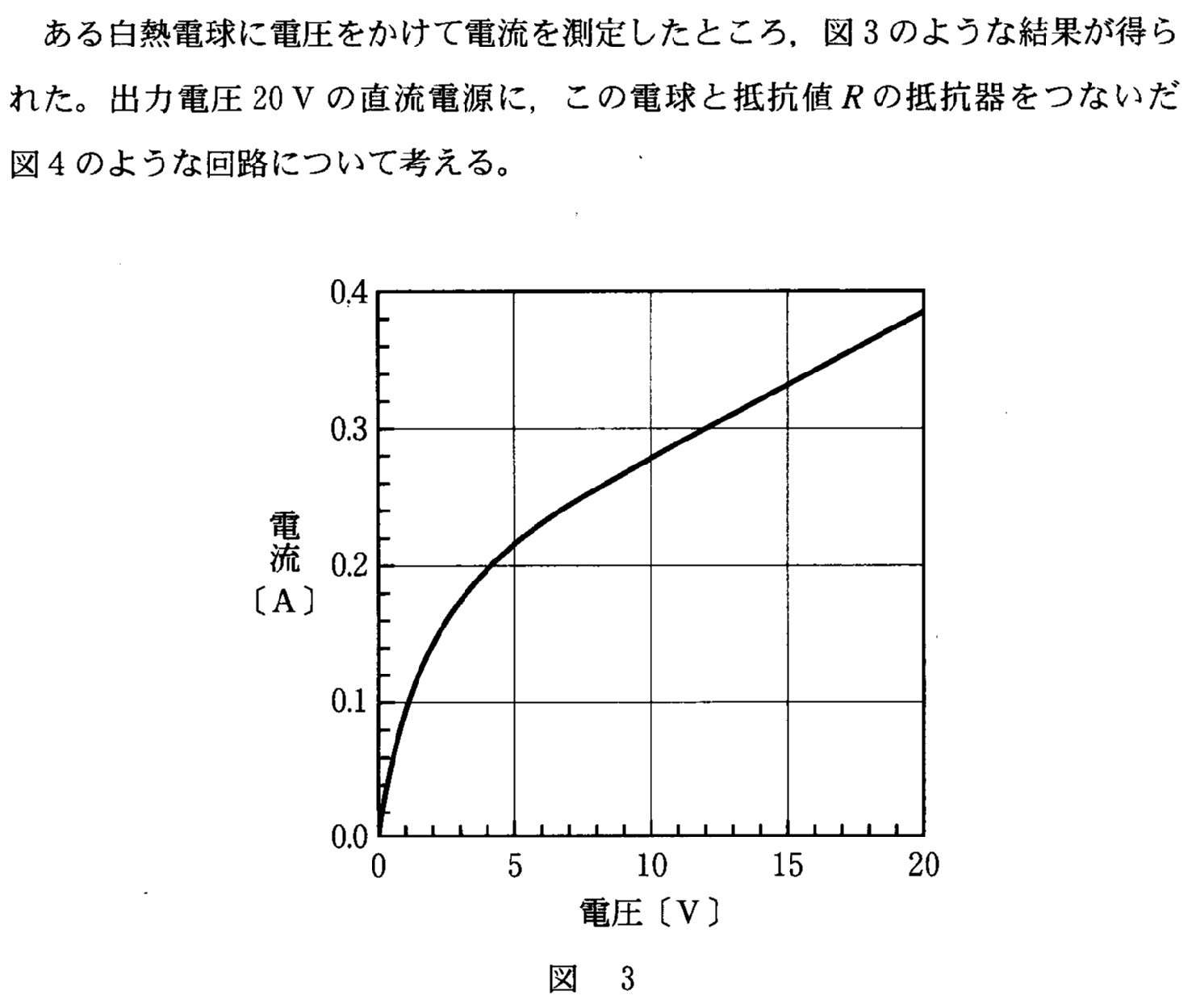
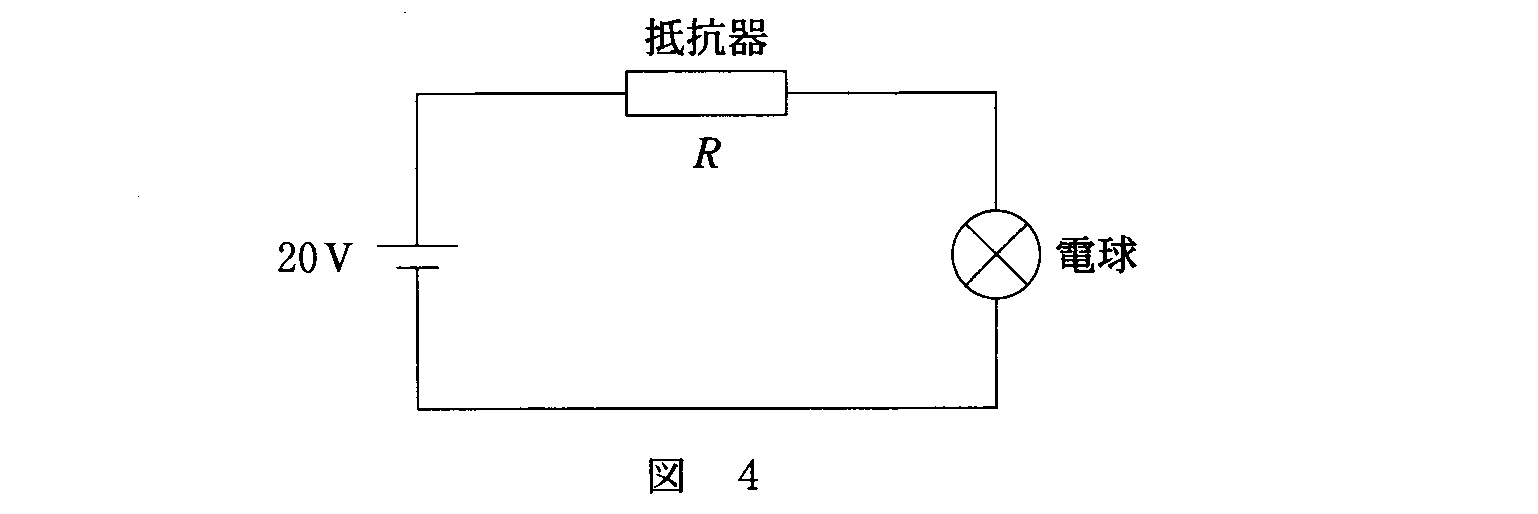


(5)(4)(センター試験・2008追2B)
- 両端にかかる電位差と、流れる電流の間に、「オームの法則」のような比例関係が成り立たない抵抗を、「非オーム抵抗」、「非線形抵抗」と呼ぶ。
自然界は、「比例関係」に満ちているように見えるけれど、実は「理想的」な条件を仮定した場合の「例外的」なものであることが多い。
どんな抵抗でも、「比例関係」に近似できる「定義域」があって、それを外れた過酷な条件のもとでは、成立しないことの方が当たり前だと考えた方がいいくらいだ。 - 抵抗でのエネルギー消費(ジュール熱)が大きくなるにつれて、抵抗自体の温度も上昇するから、原子核の熱振動が激しくなり、「自由電子」は通りにくくなる(!)、だから抵抗値が増える、と一応説明できる。
- 「オームの法則」の式が使えない分だけ、連立方程式を解くにあたっての「条件式」の数が減る。
これを補うために、与えられたI-Vグラフに、「キルヒホッフ第2法則」から得られた直線の式を描き込み、交点を求める、という方法をとる。 - 「問4」について。
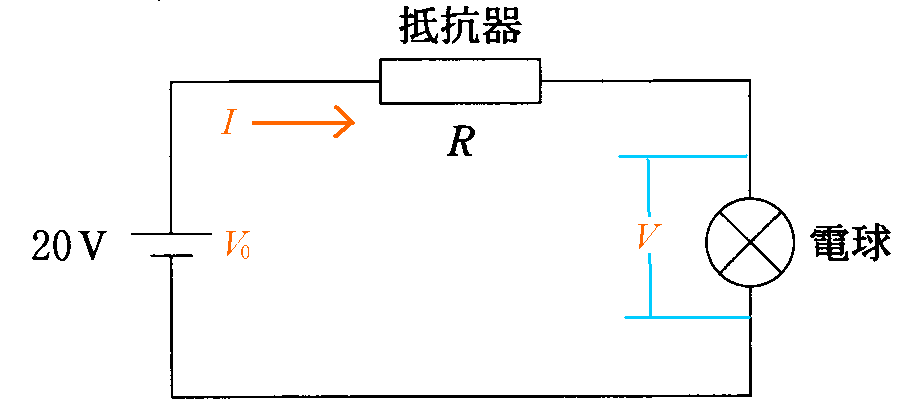
- 「電球」を流れる電流をI[A]、「電球」の両端の電位差をV[V]とする。
- 電源電圧V0=20[V]、抵抗R=50[Ω]であるから、キルヒホッフ第2法則は、
+V0-IR-V=0
すなわち、
+20-50I-V=0 - これをI-Vグラフに描き込みたいから、Iについて解くと、
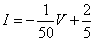
つまり「傾き」マイナス0.02、縦軸の「切片」0.4の直線である。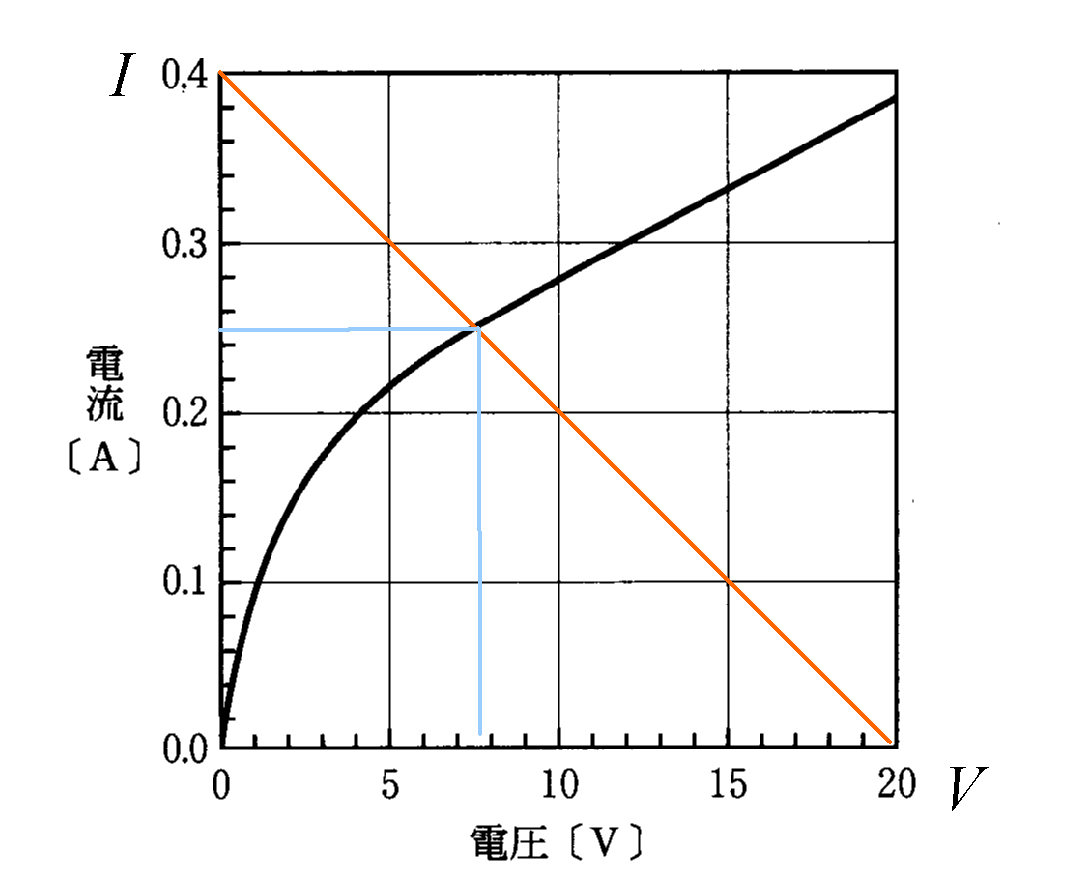
「交点」はI=0.25[A]、V=7.5[V]、したがって「1秒あたりに発生するジュール熱」[J/s]、すなわち「消費電力」は、
P=VI=7.5×0.25=1.875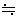 1.9[W=J/S]
1.9[W=J/S]
- 未知数は