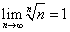(4)
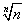
(5)
(4),(5)は、それぞれ、1,0に収束する、と推測できる。
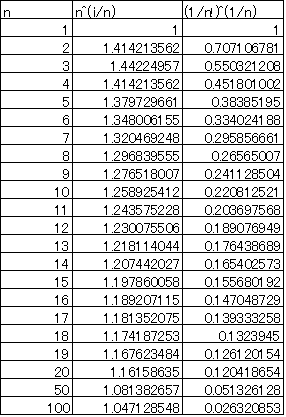
(4)
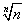が1に収束すること、すなわち、任意の正数εに対して、n＞Nならば、つねに、
|
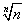-1|＜εとなるNが存在することを示さなければならない。
であるから、これが0に収束すること、を示したい。分子、分母ともに+∞に発散するから、典型的な「不定型」で、定理1.4の、出る幕はなさそうである。上の、「コーシーの収束性の定義」の「実用版」、「はさみうちの原理」に頼ることになる。
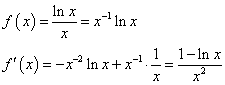
だから、この関数は、x＞0で定義されx=eで極大値をとり、以降、単調減少であり、かつ、つねに正である。いかにも0に収束しそうであるが、証明には、何か別の仕掛けが必要なようである。
x＞0の範囲で、つねにf(x)より大きく、かつ0に収束する、簡単な、関数を探し出さなければならない。
y=1/√xでは、どうだろう?
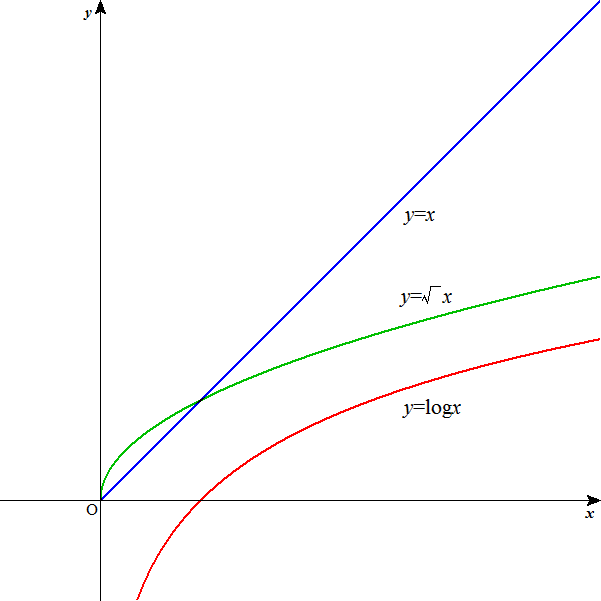
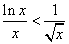を示したい。
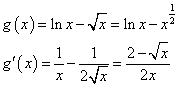とおくと、
x＞4で単調減少、よって、n＞4で、
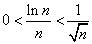
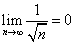だから、
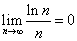すなわち、