(1)
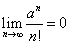
(2)
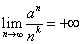
(1)任意の正数εに対して、n＞Nのとき、つねに
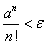となるNが存在することを示せばよい。
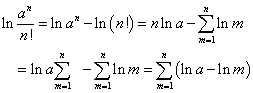
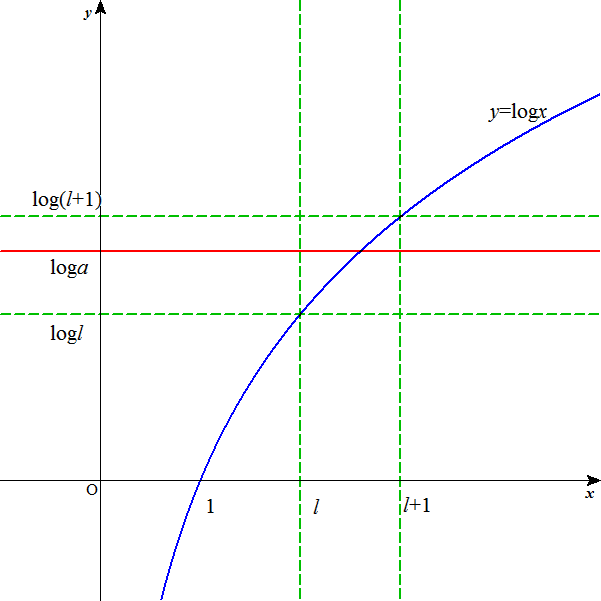
a＞1に対して、l≦a＜l+1なる自然数lが存在する。すなわち、
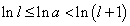
したがって、
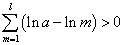・・・（ア）
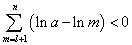・・・（イ）
ここで、（ア）は定数aによって定まる有限値であり、これに対して、（イ）の絶対値は、nを大きくすることで、いくらでも大きくできる。
したがって、
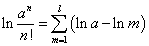を、どこまでも小さな負の値にすることができる。
すなわち、nを大きくとることで、an/n!を、1よりどこまでも小さな、正の値にすることができる。
よって、示された。
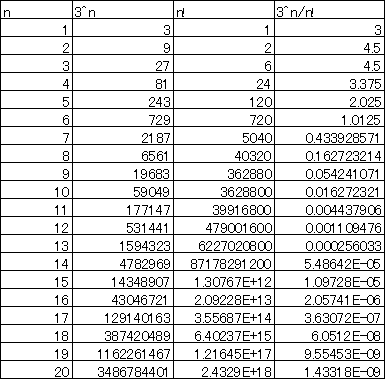
a=3として、n=20までの計算結果。
(2)任意のMに対して、n＞Mのとき、つねに、
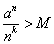
となるNが存在することを示せばよい。
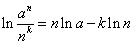
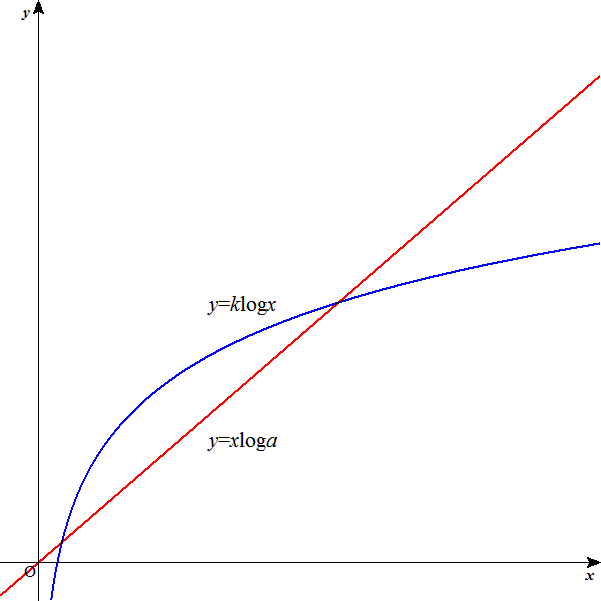
グラフからわかるように、y=xlogaは、傾きlogaの直線、y=klogxは、全区間単調増加ではあるが、つねに「上に凸」の曲線であるから、nを十分大きくとれば、両者の差は十分大きくなる。
よって、示された。