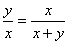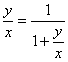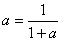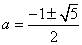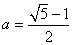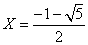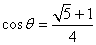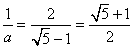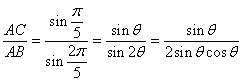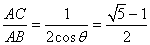5-Pointed Star/あるいは/世界の私に対する「まなざし」





私(x)の他者(y)に対する「まなざし」(y/x)が、私と他者を含む世界(x+y)の私に対する「まなざし」に等しいとすれば、
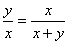
右辺の分子分母をxで割って、
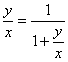
この式の値y/xをaとおくと、
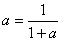
これを満たすaは次の2次方程式の解となるから、
a(1+a)-1=0
a2+a-1=0
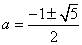
であるが、私は世界に含まれている以上、この式の値は0<a<1であり、
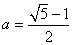
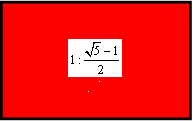
となる。この値は、a=0.618033989・・・であり、「黄金分割比」として知られている。
「部分」と「全体」の比が、「全体」ともう1レベル上の「全体」との比に等しく、・・・という風に、世界が調和的に構成されているなら、その比は「整数」と「整数」の比で表すことはできず、このように「無理数」でなければならないことになる。
人が見て最も「美しい」と感じられる長方形の縦横比は、「黄金分割比」にしたがっているのだそうで、古来から多くの美術品、建造物に採用されているといわれる。これが、「黄金分割比」に従った長方形。
私たちが日ごろ最もよく用いる長方形は、A系B系などの用紙だろうが、これは番号が一つ増えて面積が半分になっても縦横比が変わらないようにするために、√2:1=1:0.707106・・・となっている。そうでなければ裁断の際に膨大な無駄が出てしまうから。こちらが√2:1系の長方形。

黄金分割といえば、ピュタゴラス学派。ピュタゴラスは「無理数」の存在を絶対に認めなかったにもかかわらず、正五角形には異様な執着を示したといわれる。
下の図で∠AOCは、2πを5等分したものだから、2π/5=72°、
∠ABCは弧ACに対する円周角だから、その半分で、π/5=36°、
同様に∠AOB=4π/5=144°、∠ACB=2π/5=72°である。
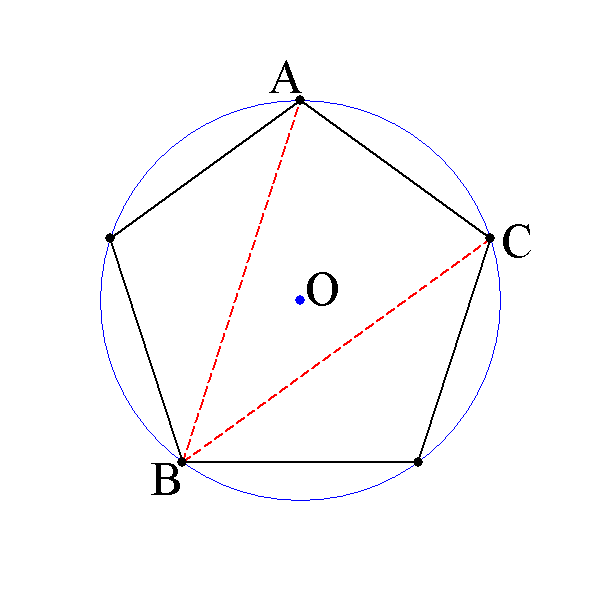
この正五角形の外接する円の半径をrとすると、「正弦定理」より、
AC=2rsin∠ABC
AB=2rsin∠ACB
である。ここで、θ=π/5とおくと、
sin2θ=sin(π-3θ)
sin2θ=sin3θ
sin2θ-sin3θ=0
sin2θ-sin(2θ+θ)=0
sin2θ-(sin2θcosθ+cos2θsinθ)=0
sin2θ-sin2θcosθ-cos2θsinθ=0
sin2θ(1-cosθ)-cos2θsinθ=0
2sinθcosθ(1-cosθ)-cos2θsinθ=0
sinθ{2cosθ(1-cosθ)-cos2θ}=0
sinθ{2cosθ(1-cosθ)-(cos2θ-sin2θ)}=0
sinθ{2cosθ(1-cosθ)-(2cos2θ-1)}=0
sinθ(2cosθ-4cos2θ+1)=0
-sinθ(4cos2θ-2cosθ-1)=0
sinθ(4cos2θ-2cosθ-1)=0
sinθ≠0であるから、
4cos2θ-2cosθ-1=0
ここで、X=-2cosθとおくと、この方程式は、
X2+X-1=0
となり、先ほどの「黄金分割比」を求めた2次方程式と同型になる。
だが、θ=π/5であるから0<cosθ<1、したがって-2<X<0であり、
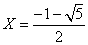
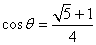
黄金分割比aには不思議な性質があって、
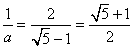
と、逆数が、相互に「共役無理数」になっている。
ではここで、正五角形の一辺(AC)と、対角線(AB)との比を求めてみる。
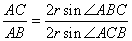
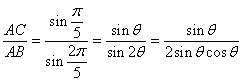
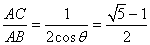
つまり、これもまた、黄金分割比となっているのだ。
フィボナッチ数列/「私を知っている私」
「エウレカ・エウレカ」
SUB-TROPICALIA
「うつログ」
「ねこログ」