フィボナッチ数列/あるいは/「私を知っている私」
二者の「関係」がある規則性をもって再現されていくとしたら、それを記述するのに少なくとも三つの「項」が必要だ。第n+2項がその前二つの項、第n項、第n+1項を用いて表現されるのを「隣接3項間の漸化式」と呼んだりする。
このうち、隣接3項間関係が1次式で表されるものに関しては一般的な解法がある。
an+2+pan+1+qan=0・・・(ア)
という漸化式があったとしよう。この式を変形して
an+2-αan+1=β(an+1-αan)=0・・・(イ)
となるようなα、βを発見することができれば、
bn=an+1-αan
と置き換えると、
bn+1=βbn
だから、これは公比βの等比数列。したがって、
bn=b1βn-1・・・(ウ)
と書ける。
ところで(イ)を変形すると、
an+2-(α+β)an+1+αβan=0
これを(ア)と係数比較すると、
α+β=-p , αβ=q
であるからこのようなα、βは次の2次方程式の解であることになる。
X2+pX+q=0
これはなんと(ア)の係数を順に並べたものに過ぎず、(ア)の「特性方程式」などと呼んだりする。
複素数解でもよいのなら、2次方程式は絶対に解ける。もう一つ大事なことは、ここまでの議論でαとβは「入れ替え可能」ということであって、(ウ)から
an+1-αan=(a2-αa1)βn-1・・・(エ)
と書けた以上、
an+1-βan=(a2-βa1)αn-1・・・(オ)
もアリだ、ということである。
で、(エ)(オ)式の両辺から式の両辺を引けば、anが得られる、つまり解けている。αとβが等しいとき、すなわち特性方程式が重解のときはこの方法は使えないが、それはそれで方法はある。さすがに少し飽きてきたので、話を進める。
さて、「フィボナッチ数列」である。ここでも先日来から懸案の「言表内容の主体」と「言表行為の主体」との矛盾にかかわる「お題」。
デカルトは「我思う。故に我在り」と言った。しかし「存在する私」と「それを知っている私」の間の「隙間」こそが、言語を用いる人間に避けがたい「病気」とつながっている。
さて、「私は存在している」「私が存在していることを私は知っている」「私が存在していることを知っている私が存在している」「私が存在していることを知っている私が存在していることを知っている」・・・という「無限」の連鎖を同様に無限な「自然数n」になぞらえて数列anに対応させ、第n項「現に存在している私」、第n+1項「それを知っている私」、そこから生成される第n+2項は「さらに『そのこと』を知っている私」であるから前2項の「和」として定義する。
隣接3項間漸化式は、その最初の2項a1 , a2については何も教えてくれないから、これらは「初期条件」として別途入力しなければならない。「一番はじめ、私が私について知っている内容」は「からっぽ」だった筈だからa1=0、「それを知った私」は、ゼロでさえなければ別に何でもよいのだがa2=1としよう。
an+2=an+1+an・・・(カ)
ただし、a1=0、a2=1
これで「フィボナッチ数列」の漸化式が完成した。解き方はもうわかっている。(ア)と比較すればp=-1、q=-1だから「特性方程式」は、
X2-X-1=0
その解は、
X=(1±√5)/2
α、βはどっちがどっちでも別にいいから
α=(1-√5)/2、
β=(1+√5)/2
としよう。
(エ)(オ)式に「初期条件」を入力すると、
an+1-αan=βn-1・・・(エ)
an+1-βan=αn-1・・・(オ)
(エ)-(オ)は、
(β-α)an=βn-1-αn-1
β-α=√5
であるから
√5an={(1+√5)/2}n-1-{(1-√5)/2}n-1
と言う訳でした。
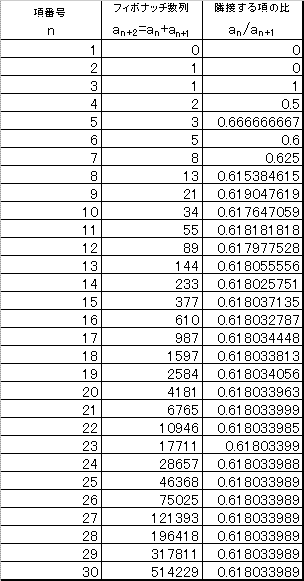
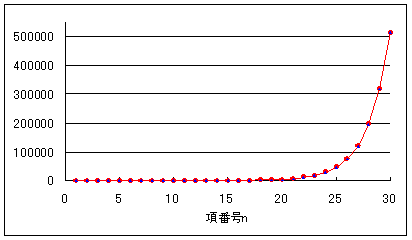
フィボナッチ数列は、ものすごい増え方をする。第30項辺りですでに五十万くらいになる。「はじめ一つがいのネズミがいて、一月に一回一つがいの子を産み・・・」みたいなのがフィボナッチ数列の例え話として引き合いに出される。すでに26匹の猫の飼い主としては避けたい話題だが、まさに「ネズミ算式」、人口増加のモデルで、グラフも指数関数とそっくりになる。
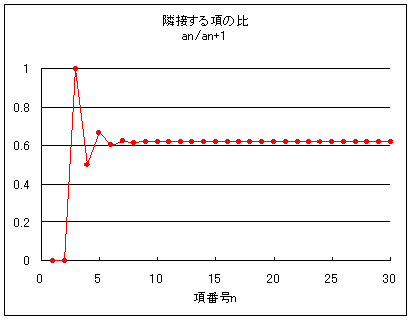
ところで「存在する私を知る私・・・」のいきつく先はどうなるのだろうか?「私が知っている私」の「割合」
an/an+1
をcnとでも定義しよう。
(カ)式の両辺をan+1で割る。
an+2/an+1=1+an/an+1
これをcnで表すと、
1/cn+1=1+cn
cnもcn+1も、十分に大きなnに対しては同じ値になるだろうからこれをCとすると、
1/C=1+C
したがって、
C(1+C)-1=0
またしても同じオチですがC>0だから、
C=(√5-1)/2
「黄金分割比」です。この収束はとても速くて、第10項くらいでこの値ともう五桁か六桁くらいぴったり一致します。
5-Pointed Star/あるいは/世界の私に対する「まなざし」
「エウレカ・エウレカ」
SUB-TROPICALIA
「うつログ」
「ねこログ」




