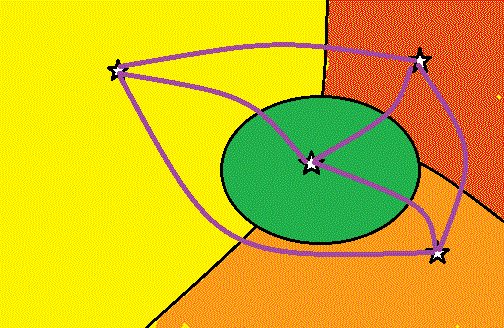
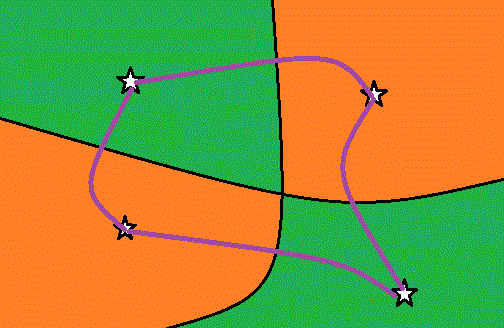
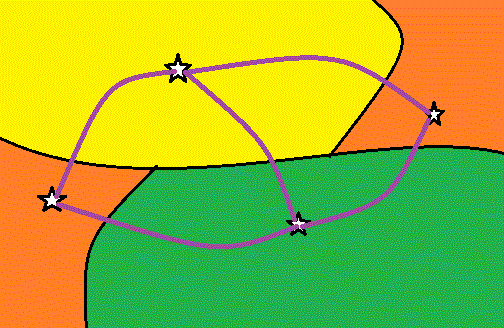
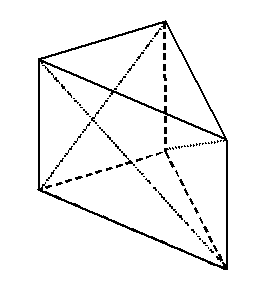
[定義]有限個の点を有限個の線で結んだ図形をグラフという。ただし線の両端は必ず点になっているものとする。グラフの点をグラフの頂点、線をグラフの辺という。片は立体交差をしていてもよいが、頂点以外では交わらない。
[定義]グラフの任意の頂点から他の任意の頂点にグラフの辺をたどっていけるとき、グラフは連結であるという。
[定義]グラフの連結成分の個数を、0次元ベッチ数という。
[定義]グラフGからうまくn本の辺を選んで取り去ってもGが連結したままだが、n+1本の辺をどう取り去ってもGが連結でなくなるとき、Gの1次元ベッチ数はnであるという。
[定義]1次元ベッチ数が0であるグラフをツリーという。
[定理]ツリーの頂点数aと辺数bの間には次の関係がある。

a-b=1

[定理(オイラー・ポアンカレの定理)]グラフGの頂点の数をa、辺の数をb、1次元ベッチ数をp1とするとき、次の式が成り立つ。

a-b=1-p1

「はじめてのトポロジー」瀬山士郎(PHPサイエンス・ワールド新書)
隣接する区画には同じ色が塗れない。隣接していない区画には同じ色を塗っても、混じりあうことがないから、かまわない。
これを何か他の問題に｢すりかえる｣ことはできないかしら？、と、トポロジーの本をぱらぱらめくっていたら、上のような一群の文章に出会った。
それぞれの区画に一つの点をとり、点同士を線で結んだら、
他の区画を経由せずに結ぶことができれば、｢隣接している｣、
他の区画を経由せずに結ぶことができなけれれば、｢隣接していない｣、
といえるではないか？

それらの点と線でできた図形を、トポロジーでいう｢グラフ｣とみなして、その｢ベッチ数｣とやらを計算してみようではないか？
隣接しない区画がある場合と、ない場合で、何か違いが見つかるのではないか？

まず、以下の図形は、すべて0次元ベッチ数は、1である。

これらは、1次元ベッチ数が0、すなわち、ツリーである。切ったら二本の線になる、当たり前だ。
a=2 , b=1 , p1=1-(a-b)=0
 

次の三つは、1次元ベッチ数が1。一ヶ所切っても遠回りして他の点にいける！、が、二ヶ所切ってしまうとばらばらになる。
a=3 , b=3 , p1=1-(a-b)=1
   

次の三つは、1次元ベッチ数が3。これらの図形が、ぐにゃぐにゃの針金でできていると想像して、一つの頂点を紙の上から浮かせて立ち上げると、｢四面体｣になる。

なるほど同じく三ヶ所切ル場合でも、真ん中の図のように切るとばらばらの立体になってしまうが、右の図のように切るとちゃんと、つながっている！、でも、もう一ヶ所切ったら、どれかの頂点が、離れる。
a=4 , b=6 , p1=1-(a-b)=3
   

いよいよ、隣接していない区画をもつ場合だ。隣接していなければ、同じ色を塗ってもかまわないのだから、あえて、同じ色を塗ってみた。
まず、｢開区画｣ばかり4つに分けて、しかも真ん中が｢点｣でつながっているから、2色しか使えない場合。
1次元ベッチ数は1。なるほど、単なる｢環｣なんだから。
a=4 , b=4 , p1=1-(a-b)=1


次は、4この｢開区画｣、二つは線を隔てて隣接しているが、そうすると当然残り二つは、隣接できない。
1次元ベッチ数は2。なるほど、2ヶ所が不通になっても、大丈夫。
a=4 , b=5 , p1=1-(a-b)=2


これらは、点が4個あるから、それらをつなぐ線は、最大4C2=6本まで引けるべきところ、それよりも線の本数が1ないし2、減っているから、1次元ベッチ数がやはり1ないし2減ってしまったのだな。

最後に、｢開区画｣3個の上に｢閉区画｣3個浮かべて、6区画にしてみた。点は6個あるから、それらから2個ずつ選んで線を引けば、6C2=15本あるべきところ、ここでは、隣接できない区画が、3対あるので、12本しか引けない！
1次元ベッチ数は8。
a=6 , b=12 , p1=1-(a-b)=8
これは、｢立ち上げて｣みると、三角柱の側面に一本ずつ対角線を書き入れた立体、と思われる。




というわけで、何がわかった！、というわけではないが、中間報告。

戻る/次