無限列数の極限に関する次の諸定理は簡単と重要とを兼ねたり。
(A) a1,a2,・・・,an,・・・
(B) b1,b2,・・・,bn,・・・
なる二つの数列の極限をそれぞれα,βとなすときは
a1±b1,a2±b2,・・・,an±bn,・・・
a1b1,a2b2,・・・,anbn,・・・
a1/b1,a2/b2,・・・,an/bn,・・・
等の無限列数の極限はそれぞれα±β,αβ,α/βなり。唯其最後の場合に於てはβが0ならざるを必要とし、又an/bn等の諸項中よりbnの0に等しきものを撤去せざるべからず。
先ず和の場合より始め、・・・
「新式算術講義」高木貞治(ちくま学芸文庫)
これはまさに「定理1.4」で、1行目がi,ii、2行目がiv、3行目「其最後の場合」がvに対応している。「先ず和の場合より始め、」と、順次証明されるのだが、iは、ここで述べたものと、寸分違わない。iiは「減法の場合亦類推すべし」と省略されている。ivの証明から、引用を続ける。
さてanbnの極限は如何。
αβ-anbn=αβ-βan+βan--anbn
=β(α-an)+an(β-bn)
Aの諸数に一定の上限あり、此上限とβとのいづれよりも(*)小ならざる数の一つを任意に採りて之をμと名づく。
今εを随意に与へ、さてε/2μを作りα-an,β-bn共に絶対的に(**)ε/2μを超えざるが如き附数の限界を定むるに、此限界以上のnにつきては
αβ-anbn
は絶対値に於てεを超えず、積の場合完了する。
「新式算術講義」高木貞治(ちくま学芸文庫)
といかにもあっさりしている。では読解を試みようとして、省略部分の数式変形をノートにペンを走らせてやってみたのだが、どうもうまくいかない。
というのは、数列(高木貞治は「列数」と呼んでいるが){an},{bn}が、いずれもすべての項が正の数でできているならば、何とかなるが、実際には、つねに負である、正と負にまたがっている、・・・、などさまざまな場合がありえ、その場合分けの深みに分け入ってしまうと、往々にして不等号の向きが望みのものと逆になってしまったりして、収拾がつかなくなる。およそ二時間ばかりも苦闘した挙句、本文(*)部分に「絶対値に於て」が抜けているのではないか?、と気づいた。「当然のこと」と省略されたものであろうが、そして、高木貞治を「訂正する」のは僭越の極み(笑)だが、そうして何とか読み解け、僭越さともども(笑)、幸福感に浸ることができたのである。したがって、(**)の「絶対的に」も、「絶対値に於て」の意味だと解釈することになる。
αβ-anbn=αβ-βan+βan--anbn
=β(α-an)+an(β-bn)
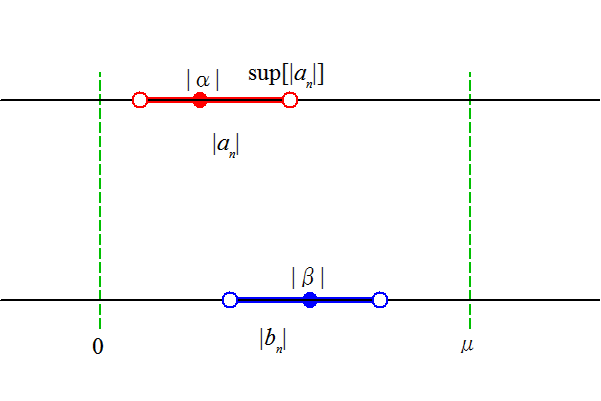
μ:{|an|}の上限、すなわち、sup{|an|}と、|β|との、いずれよりも小さくないある数、
「小さくない」は「以上」と同じことだから、
任意のnに対して、|an|≦μ
また、|β|≦μ
もちろん、μ>0
下図のようなイメージではないかと思う。もちろん、{|an|}と{|bn|}の大小関係はこうでなくてもいいし、|β|がμを超えない限り{|bn|}の上限がμを超えてもかまわない。
さて、式変形に入る。今日的な「ε-δ論法」の表現になるべく近く、翻訳してみる。
任意の正数εに対し、
n>N1ならばつねに、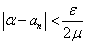 となるN1、・・・(1)
となるN1、・・・(1)
n>N2ならばつねに、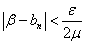 となるN2、・・・(2)
となるN2、・・・(2)
を見つけることができる。εがどこまでも小さくなれば、それを正の数2μで割った数もまた、どこまでも小さくなるからである。
このようなN1,N2のうち、より小さくないもの、max(N1,N2)を改めて、Nとすれば、
n>Nに対して、・・・、これが、上の「此限界以上のnにつきては」の意味である、
(1)の不等式の両辺に|β|>0をかけて(β≠0として)、|β|≦μであることを用いて、次のように言える。
 ・・・(3)
・・・(3)
同じくn>Nに対して、
(2)の不等式の両辺に|an|>0をかけて(an=0の場合は除外するとして)、任意のnに対して、|an|≦μであることを用いて、次のように言える。
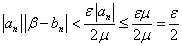 ・・・(4)
・・・(4)
ちなみに、β=0だったとしても、an=0の項に対しても、左辺が0になるのだから、それはどんな正数εよりも小さいから、問題はないと思われる。
よって、(3)(4)を辺々加えて、
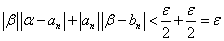
ここで、
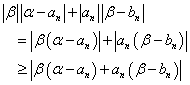
これは、|A|+|B|≧|A+B|を用いた。
したがって、
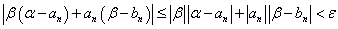
すなわち、
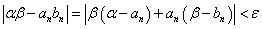
これは、nを十分大きくとれば、αβ-anbnの絶対値を、どこまでも小さくすることができることを意味している。これすなわち、
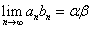 である。
である。
余りに煩雑だから、リンクを貼り付けるにとどめるが、「ここ」での証明は、私が35年ばかり前に使っていた、と言ってもほとんど開いたこともない河合良一郎他「微分積分学」の教科書に掲載されていたものを、「解読」したものなのである。
同じ基本定理の証明方法が、どうしてこんなにも異なるのだろう?
論述の流れ、筆者の数学理論上のある種の「党派的」な立場、なども関与するのだろう。ただ、思うに、「証明」と言うのは、純粋に「理論的」な操作であると同時に、相手にわからせなければならないので、必然的に「説得の技術」でもあるのだ。落語や漫才がそうであるように、観客に「お!」と言わせるには、「オチ」に趣向を凝らさねばならない。そのためには入念な「前振り」を仕込んでおく必要がある。
非常に技巧的な変形をしておきながら、どうしてそんな変形が必要だったには触れない、だって、そうなるじゃない?、なるからいいじゃない?、との「頭の良い」数学者の哄笑が聞こえると、「頭の悪い」こちらは(笑)、やや「ムカつく」わけで、・・・。
でも、さらに本質的には(笑)、数学と言うのは、そもそも、「解けることがわかっている問題を解いている」のであって、「解けた」地点から、時間を遡行して、「解き方」を、再構成しているのである。
だから数学の教科書は、上から順に、「ふんふん、なるほど」と、読める構造にはなっていない。とんでもない「断絶」や「飛躍」が随所に刻まれていて、「何故、そんなことを『思いつか』なければならないのか?」を、一時間でも二時間でも、場合によっては半日でも、数ヶ月でも(笑)、自らノートにペンを走らせ、「実験」してみないことには、「読める」わけもないのである。そんなことを、ようやくこの歳になって、人様に数学を教える、などという僭越極まりない、まことに「身の丈に合っていない」仕事から、「足を洗う」(笑)ことになってはじめて、気づいた、というお話。
商の場合の証明も興味深く、また、これらの定理の証明が、カントールが、「有理数を項とせる列数の極限として」定めた無理数の四則演算の「定義」に他ならない事実の指摘とか、・・・、まだまだ喋りたいことが多々あるが、やや疲れたので、休憩。
戻る

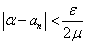 となるN1、・・・(1)
となるN1、・・・(1)
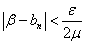 となるN2、・・・(2)
となるN2、・・・(2)
 ・・・(3)
・・・(3)
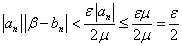 ・・・(4)
・・・(4)
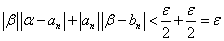
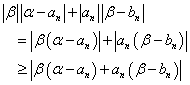
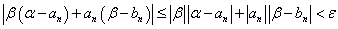
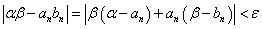
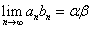 である。
である。