- まず、
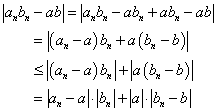
正数ε'に対して、
n>N1のとき、|an-a|<ε'となるN1が存在し、
n>N2のとき、|bn-b|<ε'となるN2が存在する。
n>max(N1,N2)のとき、|an-a|・|bn|+|a|・|bn-b|<ε'(|a|+|bn|)
ここで、ある正の定数cに対して、nが十分大きければ、|bn|<|b|+cとすることができれば、上式は、
n>max(N1,N2)のとき、|an-a|・|bn|+|a|・|bn-b|<ε'(|a|+|bn|)<ε'(|a|+|b|+c)
となるから、改めて、ε=ε'(|a|+|b|+c)とおきなおせば、式がわかりやすくなる。すなわち、
 となるが、問題は、正の定数cの大きさがわからない、というところにある。
となるが、問題は、正の定数cの大きさがわからない、というところにある。
cがかなり大きければ、N2よりずっと小さなnで|bn|<|b|+cとできるが、
cが小さく、ε'よりさらに小さくなってしまえば、N2では|bn|<|b|+cは成立しない。
そこで、次のような工夫をする。つまり、はじめから、ε'を、
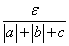 とcのうち、より大きくないもの、すなわち、
とcのうち、より大きくないもの、すなわち、
 と、定義しておくのである。
と、定義しておくのである。
以上の工夫を踏まえて、答案を書き直すと、
まず、
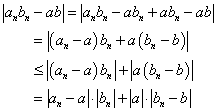
正数ε、および正数cに対して、
n>N1のとき、|an-a|<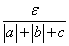 となるN1が存在し、
となるN1が存在し、
n>N2のとき、|bn-b|< となるN2が存在する。
となるN2が存在する。
n>max(N1,N2)のとき、|an-a|・|bn|+|a|・|bn-b|<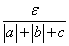 (|a|+|bn|)<
(|a|+|bn|)<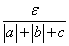 (|a|+|b|+c)=ε
(|a|+|b|+c)=ε
これは、n>N=max(N1,N2)のとき、|anbn-ab|<εとなることを意味している。
すなわち、

cは、正でありさえすれば何でもよい、たとえば、1でもよいから、次のようにも書ける。
まず、
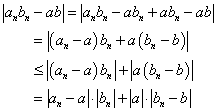
正数εに対して、
n>N1のとき、|an-a|< となるN1が存在し、
となるN1が存在し、
n>N2のとき、|bn-b|<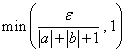 となるN2が存在する。
となるN2が存在する。
n>max(N1,N2)のとき、|an-a|・|bn|+|a|・|bn-b|< (|a|+|bn|)<
(|a|+|bn|)< (|a|+|b|+1)=ε
(|a|+|b|+1)=ε
これは、n>N=max(N1,N2)のとき、|anbn-ab|<εとなることを意味している。
すなわち、

前のページ・次のページ・補遺、高木貞治による証明
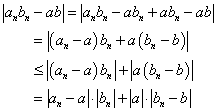
 となるが、問題は、正の定数cの大きさがわからない、というところにある。
となるが、問題は、正の定数cの大きさがわからない、というところにある。
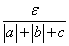 とcのうち、より大きくないもの、すなわち、
とcのうち、より大きくないもの、すなわち、
 と、定義しておくのである。
と、定義しておくのである。
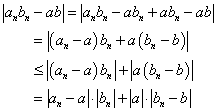
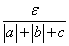 となるN1が存在し、
となるN1が存在し、
 となるN2が存在する。
となるN2が存在する。
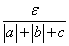 (|a|+|bn|)<
(|a|+|bn|)<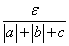 (|a|+|b|+c)=ε
(|a|+|b|+c)=ε

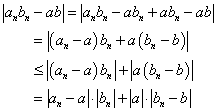
 となるN1が存在し、
となるN1が存在し、
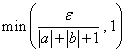 となるN2が存在する。
となるN2が存在する。
 (|a|+|bn|)<
(|a|+|bn|)< (|a|+|b|+1)=ε
(|a|+|b|+1)=ε
