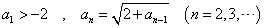---

5. [改訂版]
   のとき、を求めよ。

   ---

   
   まず、準備として、いくつかの用語の定義、と一つの定理の証明を行う。 「有界」及び「単調」について、次のように定義する。
   • 「上に有界」
     {a_n}に対して、nに無関係な定数Mが存在して、つねに
     a_n≦M
     となるとき、{a_n}は上に有界であるといい、Mを1つの上界と呼ぶ。
   • 「下に有界」
     {a_n}に対して、nに無関係な定数Mが存在して、つねに
     a_n≧M
     となるとき、{a_n}は下に有界であるといい、Mを1つの下界と呼ぶ。
   • 「単調増加」
     {a_n}が単調増加であるとは、任意のnについて、
     a_n≦a_n+1
     であることをいう。
   • 「単調減少」
     {a_n}が単調減少であるとは、任意のnについて、
     a_n≧a_n+1
     であることをいう。

   ---

   [定理]
   • 数列{a_n}が単調増加で、かつ、上に有界ならば収束する。
   • 数列{a_n}が単調減少で、かつ、下に有界ならば収束する。

   ---

   [証明]
   • {a_n}が上に有界だから、
     任意のnに対して、Mが存在して、a_n≦M
     上界Mの最小数を{a_n}の上限と呼び、sup{a_n}と書く。
     sup{a_n}=aとすると、
     上限の性質から、任意の正数εに対して、
     0＜a-a_n＜ε
     となるa-a_nが、すなわち、それに対応するnが存在する。
     一方、{a_n}が単調増加であることから、
     n＞Nに対して、a_n≧a_N
     すなわち、a-a_n≦a-a_N
     したがって、任意の正数εに対して、
     0＜a-a_N＜ε
     となるNも、当然、存在する。
     (どんな小さなεに対しても0＜a-a_n＜εとできるのなら、
     それより大きいa-a_Nにだって0＜a-a_N＜εとできていた筈だ!)
     よって、任意の正数εに対して、n＞Nのときつねに
     |a_n-a|＜ε
     となるNが存在する。
     これは、a_nがaに収束する、ということである。
   • {a_n}が下に有界だから、
     任意のnに対して、Mが存在して、a_n≧M
     下界Mの最大数を{a_n}の下限と呼び、inf{a_n}と書く。
     inf{a_n}=aとすると、
     下限の性質から、任意の正数εに対して、
     0＜a_n-a＜ε
     となるa_n-aが、すなわち、それに対応するnが存在する。
     一方、{a_n}が単調減少であることから、
     n＞Nに対して、a_n≦a_N
     すなわち、a_n-a≦a_N-a
     したがって、任意の正数εに対して、
     0＜a_N-a＜ε
     となるNも、当然、存在する。
     (どんな小さなεに対しても0＜a_n-a＜εとできるのなら、
     それより大きいa_N-aにだって0＜a_N-a＜εとできていた筈だ!)
     よって、任意の正数εに対して、n＞Nのときつねに
     |a_n-a|＜ε
     となるNが存在する。
     これは、a_nがaに収束する、ということである。
     こうして準備が完了したので、この定理を用いて、上の極限値を求める。

   ---

   前のページ・次のページ