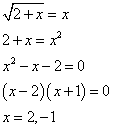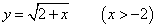 のグラフを考えると、これと直線y=xとの交点は、
のグラフを考えると、これと直線y=xとの交点は、
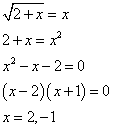
y≧0,すなわち、x≧0だから、x=2
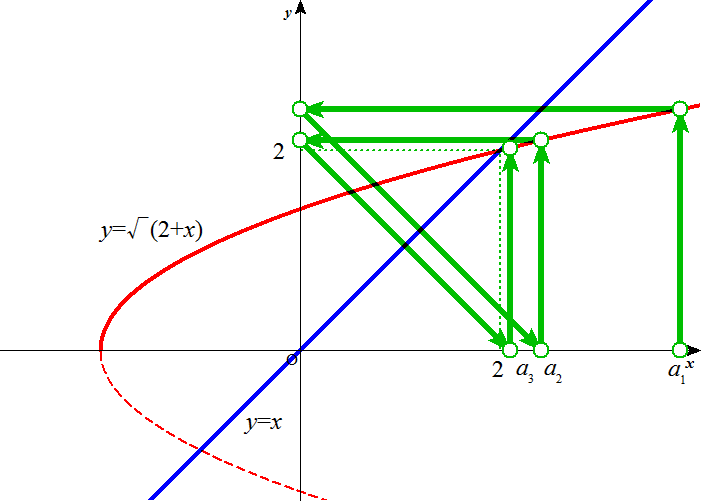
したがって、数列{an}は2に収束すると、推定できる。ただ、2の左から近づくか、右から近づくか、は、初項a1のとり方による。
- -2<a1<2のとき、数列{an}は、
- 上に有界であり、その上限が2であり、かつ、
- 単調増加である。
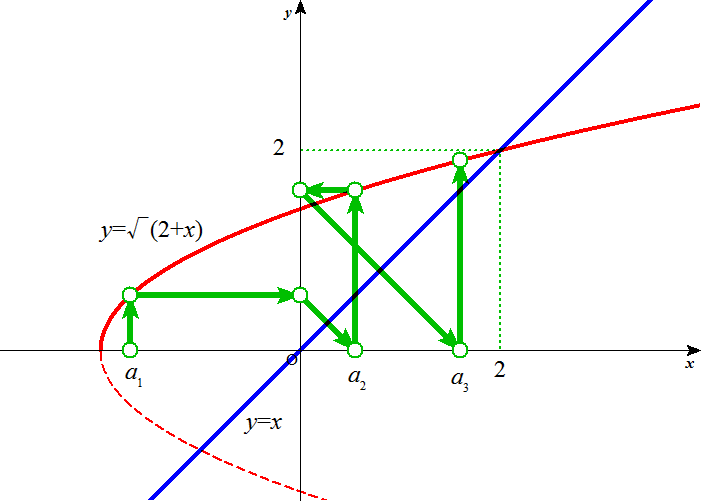
- a1≧2のとき、数列{an}は、
- 下に有界であり、その下限が2であり、かつ、
- 単調減少である。
前のページ・次のページ
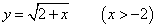 のグラフを考えると、これと直線y=xとの交点は、
のグラフを考えると、これと直線y=xとの交点は、