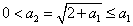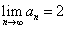- まず、{an}の単調性を示すことから着手する。

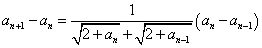 ・・・(*)
・・・(*)
ここで、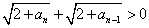 であるから、
であるから、
- a2>a1であれば、an+1>an、すなわち単調増加である。
[証明]数学的帰納法
- n=1のとき、a2>a1
- n=k-1のとき、ak>ak-1、と仮定する。
(*)より、an+1>an
i,iiより、n=1,2,・・・に対して、an+1>an
- a2≦a1であれば、an+1≦an、すなわち単調減少である。
[証明]は上と同様
- では、それぞれ、
- a2>a1
- a2≦a1
となるa1>-2の範囲を定めよう。
- a2>a1となるa1>-2の範囲を定める。
- a2≧0、-2<a1<0のとき
当然成立
- a2>a1≧0のとき
a22-a12>0
(2+a1)-a12>0
a12-a1-2<0
(a1-2)(a1+2)<0
-1<a1<2
a1≧0だから、0≦a1<2
i,iiより、a2>a1となるのは、-2<a1<2
- a2≦a1となるa1>-2の範囲を定める。
a1>-2だから、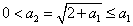
a22-a12≦0
a12-a1-2≧0
a1≦-1 , a1≧2
a1>0だから、a1≧2
a2>a1となるのは、a1≧2
以上、まとめると、
- -2<a1<2のとき、{an}は単調増加であり、
- a1≧2のとき、{an}は単調減少である、
ことが示された。
- -2<a1<2のとき
- {an}が上に有界であり、その上限が2であること、
すなわち、n=2,3,・・・に対して、an≦2であることを示す。数学的帰納法による。
- n=2のとき、
-2<a1<2
0<2+a1<4
0<√(2+a1)<2
0<a2<2
- n=k-1に対して、
ak-1≦2
と仮定すると、
2+ak-1≦4
√(2+ak-1)≦2
ak≦2
i,iiより、n=2,3,・・・に対して、an≦2である。
- {an}が上に有界であり、その上限が2であり、かつ、{an}が単調増加であることから、
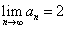
が示された。
- a1≧2のとき
- {an}が下に有界であり、その下限が2であること、
すなわち、n=2,3,・・・に対して、an≧2であることを示す。数学的帰納法による。
- n=2のとき、
a1≧2
2+a1≧4
√(2+a1)≧2
a2≧2
- n=k-1に対して、
ak-1≧2
と仮定すると、
2+ak-1≧4
√(2+ak-1)≧2
ak≧2
i,iiより、n=2,3,・・・に対して、an≧2である。
- {an}が下に有界であり、その下限が2であり、かつ、{an}が単調減少であることから、
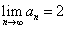
が示された。
I,IIより、いずれの場合も、
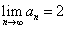
前のページ・次のページ

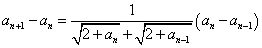 ・・・(*)
・・・(*)
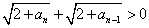 であるから、
であるから、