7. 
   「公理IIの2条件」の内容が不明なので、これを、以下の｢カントール(Cantor)の公理｣と解して、若干問題を作り変えてみた。

   ---

   0＜a＜bとする。2つの数列{a_n},{a_n}を次のように定める。
   
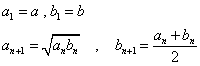
   • (1)  任意の自然数nに対して、a_n＜b_nを示せ。
   • (2)  閉区間I_n=[a_n,b_n]とすると、I_n+1⊆I_nを示せ。
   • (3) 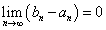 を示せ。
   • (4)  {a_n},{b_n}は収束し、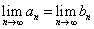であることを示せ。

   ---

   カントール(Cantor)の公理
   • 閉区間の無限列I_nが、
     I₁⊇I₂⊇・・・⊇I_n⊇I_n+1⊇・・・
     をみたしていて、かつ、
   • iが無限に大きくなるときI_iの幅が0に収束するならば、
   すべてのI_iに共通に含まれる実数αが、ただ一つ存在する。

   ---

   問(2)は、｢カントールの公理｣の前半の条件、閉区間の無限列の存在の証明、
   問(3)は、｢カントールの公理｣の後半の条件、閉区間の幅が0に収束することの証明、
   を、それぞれ要求している。ここから、｢カントールの公理｣より、
   任意のnに対応する閉区間I_nに共通に含まれるただ一つの実数αの存在が導かれ、
   問(4)で、{a_n},{b_n}ともに、そのαに収束することを導く。

   ---

   (1)
   n=1,2,3,・・・に対して、a_n＜b_nを示す。数学的帰納法による。
   1. n=1のとき、a＜bすなわち、a₁＜b₁
   2. n=kのとき、a_k＜b_kと仮定する。
      
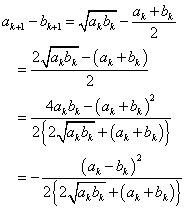
      あきらかに、a_k＞0,b_k＞0だから、a_k+1＜b_k+1
      n=k+1のときも成立する。
   i,iiより、n=1,2,3,・・・に対して、a_n＜b_nが示された。

   ---

   (2)
   I_n+1⊆I_nすなわち、a_n≦a_n+1＜b_n+1≦b_nを示したい。
   
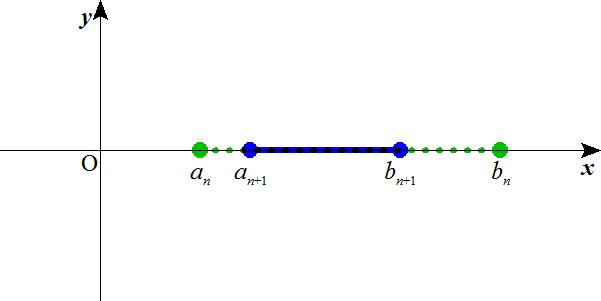
   • (1)より、a_n+1＜b_n+1である。
   • a_n≦a_n+1を示す。
     (1)より、0＜a_n＜b_nだから、
     0＜a_n²＜a_nb_n
     0＜a_n＜√a_nb_n
     0＜a_n＜a_n+1示された。
   • b_n+1≦b_nを示す。
     (1)より、0＜a_n＜b_nだから、
     0＜a_n+b_n＜2b_n
     0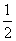＜(a_n+b_n)＜b_n
     0＜b_n+1＜b_n示された。
   よって、a_n≦a_n+1＜b_n+1≦b_nすなわち、I_n+1⊆I_nが示された。

---

前のページ・次のページ