(1)より、0＜an＜bnだから、
0＜an2＜anbn
0＜an＜√anbn
-2an＞-2√anbn
-an＞an-2√anbn
bn-an＞bn+an-2√anbn
すなわち、
(an+bn)-2√anbn＜bn-an
ここで、
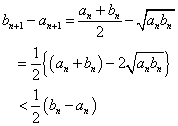
したがって、
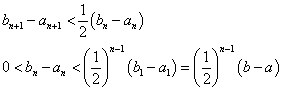
一方、
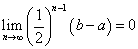
｢はさみうちの原理｣から、
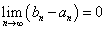
(4)
- (2)より、閉区間の無限列Inが、
I1⊇I2⊇・・・⊇In⊇In+1⊇・・・
をみたし、 - (3)より、iが無限に大きくなるときIi=[ai,bi]の幅が0に収束する、
「カントールの公理」より、すべてのIiに共通に含まれる実数αが、ただ一つ存在する。
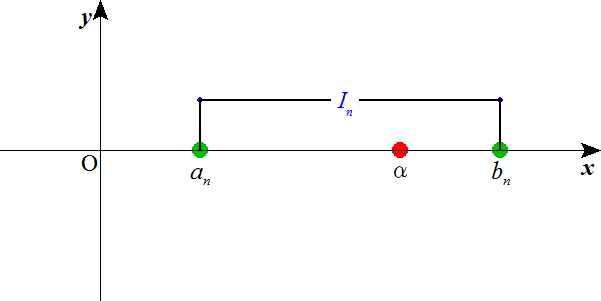
このαに対して、
- 任意の正数εに対して、n＞Nのとき、
α-an＜ε
となるNが存在する。すなわち、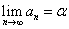
- 任意の正数εに対して、n＞N'のとき、
bn-α＜ε
となるN'が存在する。すなわち、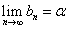
よって、{an},{bn}は収束し、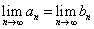
であることが示された。
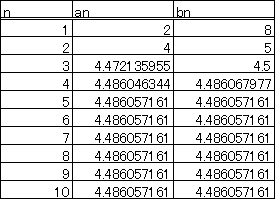
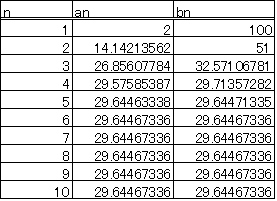
[例]a1=2,b1=8,a1=2,b1=100の2つの場合について、第10項まで計算してみた。
収束はかなり速いようである。この極限が｢算術幾何平均｣ということになる。
(｢算術平均｣は｢相加平均｣、｢幾何平均｣は｢相乗平均｣の、それぞれ古風な言い方である。)
