[定義]部分列
自然数の無限列n1＜n2＜・・・＜ni＜・・・に対して、
数列{an}の第ni項を第i項とする数列{ani}を、数列{an}の部分列という。
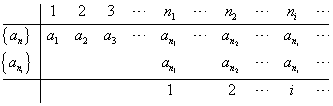
[証明]
{ani}を{an}の部分列とする。
任意の自然数に対して、ni≧iである。
また、
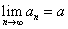であることから、
任意の正数εに対して、n＞Nならば|an-a|＜εとなるNが存在する。
ここで、i＞Nとなる自然数iを考えれば、
ni≧i＞N
であるから、このようなniに対して、
|ani-a|＜ε
とできる。これは、{ani}がaに収束することを意味する。
[例]具体例を考えてみる。
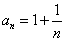とすると、
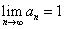である。
また、ni=2iとする。
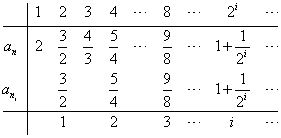
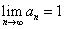であるから、
任意の正数εに対して、n＞Nならば|an-1|＜εとなるNが存在する。
たとえば、ε=0.001として、これに対応するNを求めてみる。
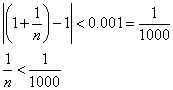
n＞1000すなわち、N=1000
これは、第1001項以降、数列{an}の各項は、0.999と1.001との間に収まっていることを示している。
ではここで、iとして、1001を選ぼう。
ni=21001であり、
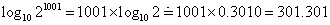より、
10301＜21001＜10302であるから、この数は、10進法で302桁、
i=1001よりはるかに大きい。
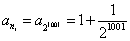であるから、
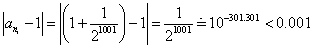
は、当然みたされるのである。
同じε=0.001に対して、部分列{ani}の何項目以降から
|ani-1|＜ε
が成り立つか、調べてみると、
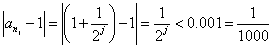
2j＞1000すなわち、j≧10
つまり、部分列{ani}の各項は、すでに、第10項目以降、0.999と1.001との間に収まっているのである。