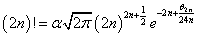m=1,2,3,・・・、n=1,2,3,・・・に対して、
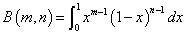
を｢ベータ関数｣と呼ぶ。この定積分を直接計算することは、おそらく(笑)不可能だから、nに関する漸化式を得ることによって、解きたい。
n=2,3,4,・・・に対して、
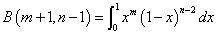
次のような部分積分を施して、
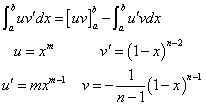
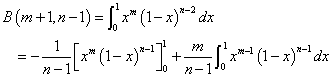
右辺第1項は0だから、
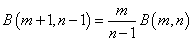
この漸化式を解こうと思う。ここで、0≦x≦1、m=1,2,3,・・・、n=2,3,4,・・・に対して、両辺の被積分関数はいずれも、
xm-1(1-x)n-1≧0
xm(1-x)n-2≧0
で、負にならないから、
B(m,n)＞0 , B(m+1,n-1)＞0
そこで両辺の対数をとって、
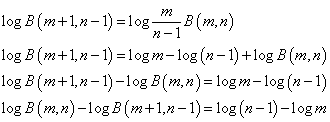
これについて、以下のように、番号をひとつずつずらして足し算すると、
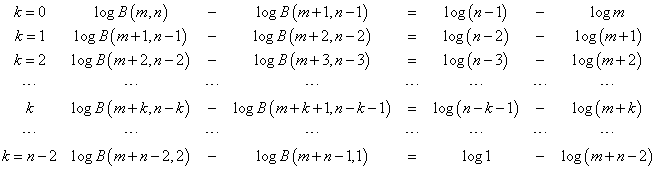
以下のようになって、
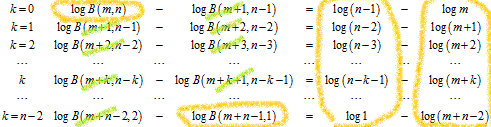
ここで、右辺の和はそれぞれ、以下のように表すことができる。
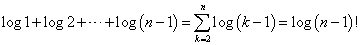
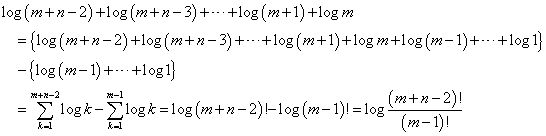
したがって、
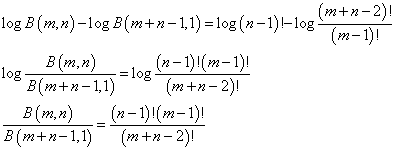
ここで、
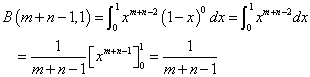
であるから、こうして｢ベータ関数｣の一般式を得ることができた。
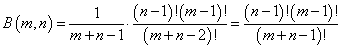
ちょっと脇道に逸れるが(笑)、これを用いると、たとえば、
m=0,1,2,3,・・・、n=0,1,2,3,・・・に対して、
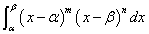
を計算することができる。
s=x-αなる置換積分を施すと、α≦x≦βに対して、0≦s≦β-α、
ds/dx=1であるから、
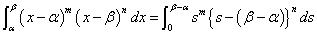
さらに、t=s/(β-α)なる置換積分を施すと、0≦s≦β-αに対して、0≦t≦1、
dt/ds=1/(β-α)であるから、
となって、｢ベータ関数｣と関連付けることができそうな按配である。
であるから、m=i-1,n=j-1 、 m=0,1,2,3,・・・、n=0,1,2,3,・・・に対して、
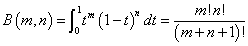
よって、
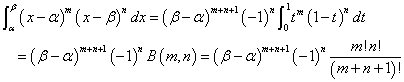
を得る。これはたとえば、m=1,n=1のとき、
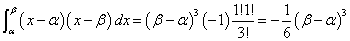
であり、有名な(笑)、アルキメデスの発見による、と言われる、放物線とその割線によって囲まれた面積の公式、なのであった。
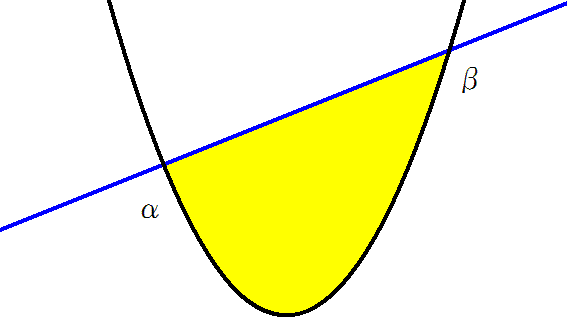
調子に乗ってやってみると、
α=-1,β=3として、
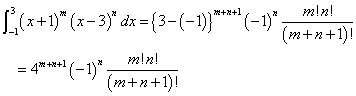
m=6,n=2のとき、
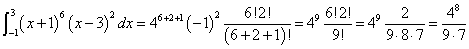
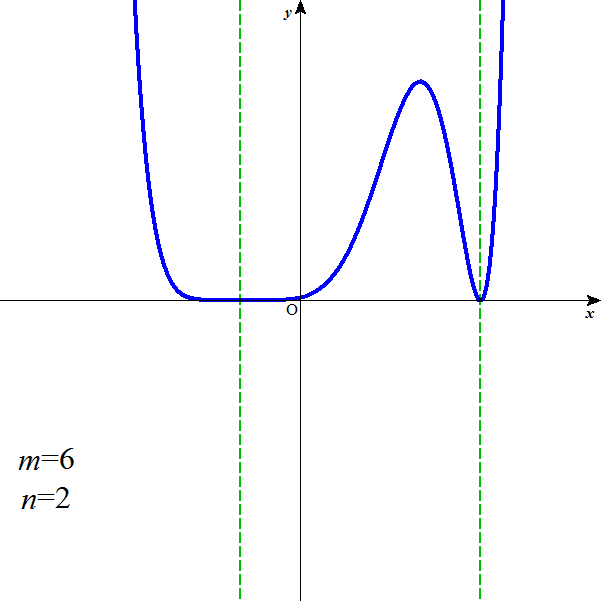
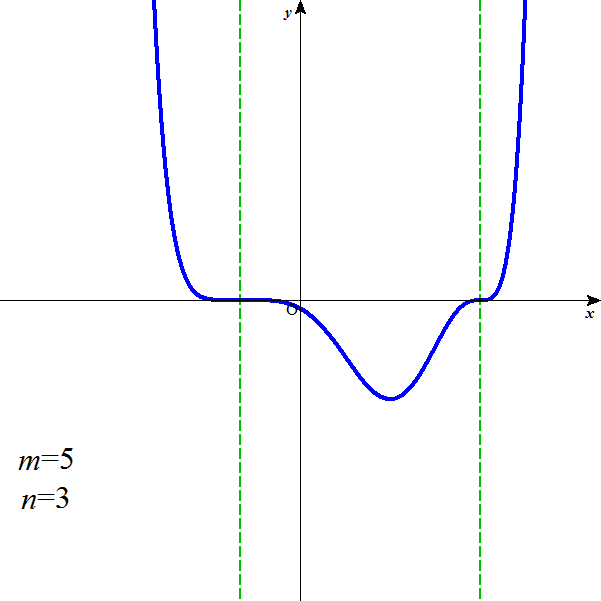
m=5,n=3のとき、
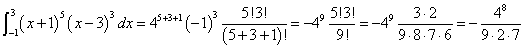
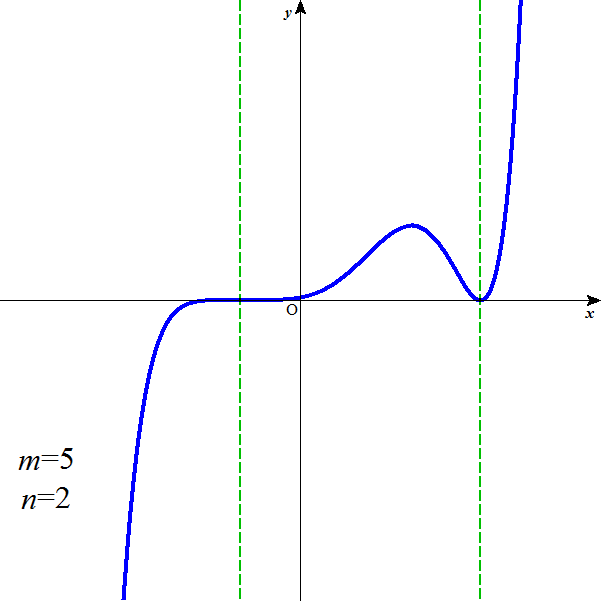
m=5,n=2のとき、
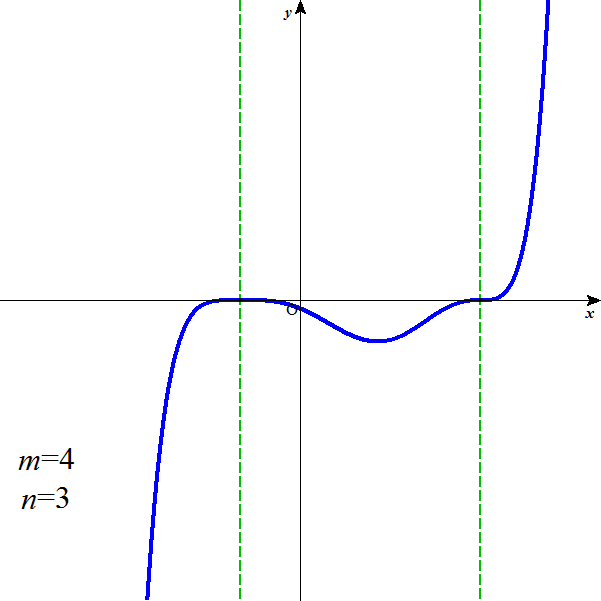
m=4,n=3のとき、
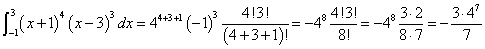
正数nに対して、
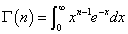
と呼ぶ。この積分も、n=1以外は、計算できなさそう(笑)であるから、漸化式を得ることによって、その｢意味｣が明らかになることになる。
まず、n=1のとき、
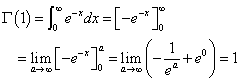
一般のnについては、以下のような部分積分を行う。
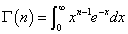
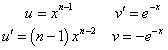
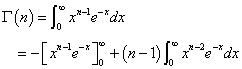
ここで、右辺第1項が収束してくれるのならば、第2項の積分はΓ(n-1)そのものだから、これで漸化式が得られたことになる。
やや回り道になるが、では、右辺第1項が収束する、実は、0に収束するのだが、ことの証明を行おう。すなわち、
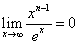
を、示したい。そのためには、こんな技巧を施さねばならない。｢はさみうちの原理｣に持ち込むための不等式を作り出すのである。
x≧0ならば、n=1,2,3,・・・に対して、
であることを示す。
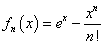
とおく。微分すると、n=2,3,4,・・・に対して、
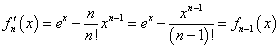
となる。実は、
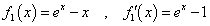
であるから、この式はn=1に対しても成り立つのである。ただし、そのためには、0!=1であることを、知らなければ、あるいは、0!=1にしなければ(笑)ならないのだが、それこそが、「ガンマ関数｣から定義されるのであって、その話はのちにする。
x≧0ならば、n=1,2,3,・・・に対して、fn(x)＞0であることを示す。数学的帰納法による。
- n=1のとき、
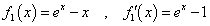
であるから、x≧0に対して、f1'(x)≧0・・・(1)
また、f1(0)=1＞0・・・(2)
(1)(2)より、x≧0に対して、f1(x)＞0
これは、(2)左端x=0、で既に正、あとは(1)単調増加、だから、ずっと正、ということを言っている。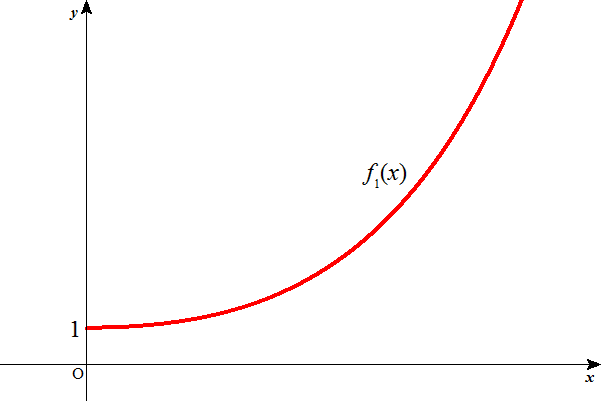
- n=kのとき、x≧0に対して、fk(x)＞0と仮定する。
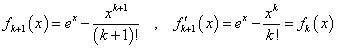
であるから、仮定より、x≧0に対して、fk(x)＞0・・・(1)
また、fk+1(0)=1＞0・・・(2)
(1)(2)より、x≧0に対して、fk+1(x)＞0
n=k+1のときも成立することがわかった。
x≧0ならば、n=1,2,3,・・・に対して、
ここで、x＞0として、両辺をxex＞0で割り、かつ、n!＞0をかける、という変形を行うと、
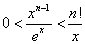
が得られる。ここで、
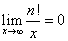だから、｢はさみうちの原理｣より、
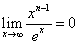
話を戻して、これで下の式の右辺第1項は0に収束することがわかったから、
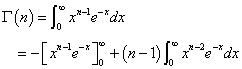
すなわち、
Γ(n)=(n-1)Γ(n-1)
これが、｢ガンマ関数｣の姿である。
思い出しておきたいのは、｢ガンマ関数｣の定義が、
正数nに対して、
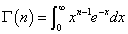
であって、紛らわしい文字使いではあるが、nを少しも｢自然数｣とは言っていないことである。
正の実数ならば何でもよいのであるが、もちろん、自然数であっていけない理由もない。
Γ(1)=1であったから、得られた漸化式から、自然数についての｢ガンマ関数｣の値は順次求められる。
Γ(2)=1・Γ(1)=1・1=1
Γ(3)=2・Γ(2)=2・1=2
Γ(4)=3・Γ(3)=3・2=6
・・・
なんと、これは｢階乗｣そのものではないか?
自然数nに対しての｢ガンマ関数｣Γ(n)は、
Γ(n)=(n-1)!
であり、ということは、｢ガンマ関数｣は、｢階乗｣の、自然数以外の正の実数への拡張、という意味をもつことになる。
とすれば、0!=1も、すんなり(笑)理解できる。
Γ(1)=0!=1ではないか？、と。でも、これは事態の半分しか説明していない、と、私は(笑)思っている。
｢階乗｣という操作は、ある自然数から初めて順次1を引いた数を掛け算していき、1になったら終了せよ、という命令なのであるから、ゼロの「階乗」という言葉自体語義矛盾なのである。
でも、数学は、つねにそういう日常用語上は矛盾としか思えない用語を用いて、概念の｢拡張｣を行ってきたのだ。
足しても変らない数を0という、いやそれは｢足した｣ことになってない！、
かけても変らない数を1という、いやそれは｢かけて｣ない!、
要素をもたない集合を空集合という、いやそれは｢集合｣ではなかろう?
という具合に。
こうして拡張を行う際には、二つの側面があるように思える。
まず、それを入れておかなければ、｢困る｣から、入れた。この段階では、ほぼ｢無理由的｣なのである。
で、あとから、拡張してみたら、つじつまが、合っていた。無論、つじつまが合うように、決めたのである。
なんだか、ちょっともどかしい(笑)言い方だが、だから、Γ(1)=1であることが、0!=1の、｢理由｣では、ないのである。そう言ったら、本末転倒なのである。
｢理由｣は、他にあったはずだ。そうでないと、是非とも0!=1でなければ、｢困る｣ような｢理由｣が、・・・。
他の例を挙げてみる。
20=1なのは、なぜか?
2-3という表記法を、23の逆数を表すと約束して採用したとき、当たり前だ、2を｢-3｣回かけるなどという行為を想像することができない、・・・、
その瞬間に、20=1でなければならなくなったのは、｢指数法則｣、
am・an=am+n
を、｢守りたかった｣からなのね。だって、
23・2-3=1
なのは定義上、「約束｣の上で、そうならざるを得ないんだから、今度は、
23・2-3=23-3=20=1
にしないと｢いけない｣でしょ?
もう一つ、1はどうして｢素数｣ではないのですか?、｢素数｣の定義は、｢1とそれ自身以外に約数をもたない｣であるから、1も該当しない、とは言えない、だからこそ、｢ただし、1は除く｣と但書を付加しなければならないのである。
これも、｢そうしなかったら、とても、困る｣事情を探ればよい。
もし1が素数であったなら、素因数分解の一意性が、失われてしまうのである。
28=22・71
であるが、1をも素数というのならば、もちろん｢屁理屈｣ではあるが(笑)、
28=110・22・71でも、28=1100・22・71でも、いくらでも言えてしまうじゃないか?
では0!=1でないと｢困る｣事情は、なんだろう?
順列nPrの定義にあるのだと、思っている。
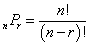
という式を｢読んで｣みよう。n枚の異なるカードがあって、これを左から順に並べていく。一番左に選べるカードはn枚あるが、並べてしまうとその隣には、もはや(n-1)枚の選択肢しかない、3番目は(n-2)枚、と順次減っていく、・・・、
そうすると、n枚全部を並べきるのには、n(n-1)(n-2)・・・3･2･1通りの方法があることになろう。この数の｢表記法｣として、｢階乗(!)｣が採用されたのである。
では、n枚全部を並べるのではなく、途中で、たとえばr枚目でやめたとすれば?
これは、後攻のチームが勝っているときは9回裏を｢やらない｣、商店街のくじ引きであたりが全部出てしまったら、もう誰も｢引かない｣、などの例を想像するとよいが、いや、別に9回裏、やってもいいのである、はずればかりとわかっていても、最後まで、引いてもいいのである。
ここでも、(r+1)枚目以降n枚目は、並べても、並べなくても、同じなのである。だから、その、(n-r)枚の並べ方は、｢重複｣として除去しなければならない、だから、
n!を(n-r)!で、割るのである。
さて、0!=1でないと「困る」のは?、もちろんr=nの場合である。0!=1と｢約束｣しておかないと、このとき、順列の｢公式｣が使えなくなってしまうではないか?
m=1,2,3,・・・、n=1,2,3,・・・に対して、
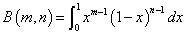
を｢ベータ関数｣と定義する、として、そこから漸化式を作って、
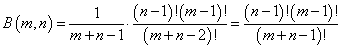
を得た。もちろん、これは｢階乗｣の記号｢!｣を用いている以上、m,nは自然数であることが前提であった。
一方、｢ガンマ関数｣は、
正数nに対して、
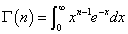
と定義され、その漸化式は、
Γ(n)=(n-1)Γ(n-1)
であり、nが自然数のときに限って、
Γ(n)=(n-1)!
とこれまた｢階乗｣を用いて表現できるのである。
ならば、m,nがともに自然数であるなら、
Γ(n)=(n-1)!
Γ(m)=(m-1)!
Γ(m+n)=(m+n-1)!
であるから、
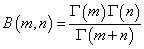
となるではないか？、ちゃんと｢ベータ関数｣と｢ガンマ関数｣は、関連付けられるのである。
それだけのこと(笑)なら、どうして｢ガンマ関数｣の式が、あんな物々しい｢ネイビア数｣まで登場する｢異常積分｣、積分区間の一方が無限大だから、そんなもの収束性を確認しなければ軽々しく用いることはできない、という意味で｢異常｣なのだ、私はそんなことすら(笑)この歳まで、知らなかったが、・・・、定義式でなければならないのか?
どうやらそれはひとえに、自然数ではな・い・、mやnに対して、｢ガンマ関数｣の値を得たい、それが｢動機｣であるらしいのだ。
上の、
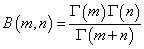
は、任意の正数m,nに対して、成立する。ただ、そこへ至るには、｢ベータ関数｣、｢ガンマ関数｣の定義式に、何かとんでもなく不可解な(笑)変数変換を施さねばならず、さらに右辺の分子Γ(m)Γ(n)の部分に登場する｢二重積分｣はいずれにしても解くことはできないのだが、極座標に変換すると、少しは見えやすい形になる、そのためには、｢面積要素の比率｣を知らねばならず、ここに「関数行列式Jacobian｣なるものが登場する、・・・、等々の段取りで、これらのこと一切、数理統計学の教科書には、わずか半ページに記載されているのだが、それをただ｢読む｣ために一週間以上の時間と、ノーと丸々二冊が必要だったわけで、まことに｢失業者｣のみに許された｢贅沢｣と言えよう(笑)。
結論を少し先取しておくと、上式が自然数でない正数にもm,nにも、成立するとしよう。
m=n=
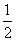のとき、
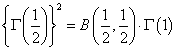
となり、Γ(1)=1であり、また、これはのちに説明するが、
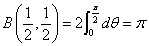
であるので、なんと、
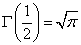と言う不気味なことが起るのである。
正規分布確率密度関数の式の係数に、√πがくっついていることだ・け・は、おぼろげに記憶していた。
その由来は、ここにあったようなのである。何故、この世の多くの事象がその形をたどると言われている｢正規分布｣に、円周率が登場するのだ?、もちろん、その｢何故｣に答えられるわけではない。ただただ、そうなっているからそうなのだ、と｢受け容れ｣ねば(笑)ならず、ほぼ｢気持ちが悪い｣ほどの｢自然の妙｣に(笑)、へらへらと心打たれるしか、ないのである。
自然数m,nに対しては成立することがすでにわかっている次式、
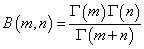
が、任意の正数m,nにも拡張されることを示したい。
｢ベータ関数｣、正数m,nに対して、
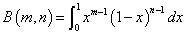
｢ガンマ関数｣、正数nに対して、
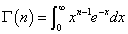
これら双方の定義式に対して、変数変換(置換積分)を施す。なぜ、そのような変換を用いるのか?、には勿論｢動機｣がある筈だ。そうしてみたら、うまくいったから、でもよいのだが、それを｢知る｣には、｢試行錯誤｣が必要で、ところが素人は(笑)、どのような｢試行｣を行えば、どのような｢錯誤｣が生じるか?、の想像力さえ、ないのである。そして、こんな｢試行｣からはあんな｢錯誤｣が生まれる、ということが｢わかって｣いるのならば、もはやそれは｢試行錯誤｣ではなく、計画的な｢実験｣と呼んでもいい。
まことに、数学は、すでに答えがわかっている問題を、｢解いて｣いる、という｢循環｣が、ここにもある。科学者は、実験によって未知の事柄を｢発見｣するのではない。すでにわかっていることを立証するために実験計画を立て、まさにその通りだ、と確認するのである。
｢発見｣はむしろ、実験計画の｢失敗｣によってもたらされる。｢予見｣を超える事態によってはじめて、それまで有していた｢語彙｣＝選択肢の集合＝パラダイムparadigm、を拡張せざるを得なくなるのである。｢ポスト・モダン｣時代の有名な(笑)、トーマス・クーン｢パラダイム・シフト｣は、だいたい(笑)そんなことを言っていた筈だ。
そもそも｢予見｣すらできない、頭の悪い凡人は、ともかく｢言われる通り｣にやってみて、「あ、ほんまやぁ」と、阿呆のように驚くしかない(笑)。
やってみよう。
｢ガンマ関数｣の方から。
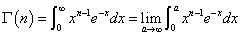
x=y2、ただしy≧0、なる変数変換を行う。
0≦x≦aに対して0≦y≦√a、dx/dy=2yであるから、
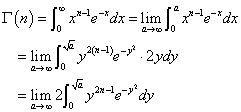
すなわち、
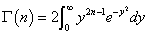
次に、｢ベータ関数｣。
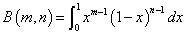
x=sin2θ、ただし、0≦θ≦π/2、なる変数変換を行う。
0≦x≦1に対して0≦θ≦π/2、dx/dθ=2sinθcosθであるから、
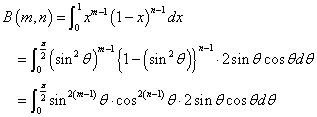
すなわち、
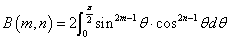
準備は、一応、整った。証明すべき式、
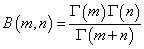
を若干変形、
Γ(m)Γ(n)=B(m,n)Γ(m+n)
として、左辺から右辺を導くことを考える。実行に移す前に少し想像してみよう、勿論私は既に｢結論｣を知っているからこそ、そんな｢偉そうに｣言える(笑)、・・・、
左辺も右辺も、それぞれ二つの定積分の積、それぞれの積分変数を変えておけば、｢二重積分｣、｢面積積分｣と見ることができる。
左辺は、｢ガンマ関数｣の積だから、積分変数は適当に名付けるとして、xとかyとかの累乗と、「ネイピア数」eのマイナスxとかyとかの2乗、との積、という形、
右辺は、｢ベータ関数｣と｢ガンマ関数｣の積だから、xの累乗、「ネイピア数」eのマイナスxの2乗、sinθの累乗、cosθの累乗、これらの積、という形になる。
ならば、左辺のx,yを、｢極座標｣に変換して、x=rcosθ,y=rsinθとすれば、
右辺は、rの累乗、「ネイピア数」eのマイナスrの2乗、sinθの累乗、cosθの累乗、となって、つながりができそうな｢予感｣がするではないか?、もちろん、既に知ってしまった｢結果｣から、時間を遡及して言っている(笑)。
というわけで左辺のΓ(m)は変数x、Γ(n)は変数y、であらわし、
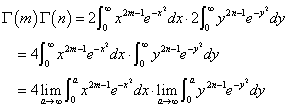
の二つの積分を合体して｢二重積分｣、xy平面上の｢面積積分｣にする。
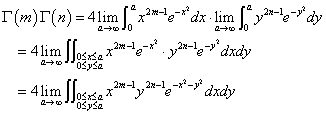
元来、相互に｢独立｣だったx,yがそれぞれ単独に「無限化」されるのだから、ともに0≦x≦a,0≦y≦aなる同じ積分区間を設定し、しかるのち、aを無限化してもいいではないか?、ということである。
上に述べた｢計画｣どおり、これを｢極座標｣に変換するのだが、1変数の積分で｢置換積分｣と呼ばれる手続きにおいて、たとえば、dtとdxの関係式を得るステップに対応するのが、2変数の｢二重積分｣では、｢面積要素の倍率｣というものに変容する。
私は、自慢ではないが(笑)、理工系の大学院というところを、決して修了はしなかったが、入学試験に合格だけはしているのである。だからそんなことすら｢知らない｣などということは、有り得ない、ことなのであるが、・・・、実に、これが、｢初耳｣(笑)、なのであった。
で、それは、長くなるので、次回のお楽しみ、｢時間｣だけは、多分(笑)、たっぷり、ある。全部書いてしまったら、書くことがなくなって｢困る｣、とも言う。
その「外積」、a×b=|a||b|sinθ・nとしてベクトル量で表される。
ただし、θはベクトルa,bのなす角、nは、ベクトルaをベクトルbに重ねるべく、θ回転したとき、その回転を「右ねじ」の回転に見立てたとき、「右ねじ」の進行方向の単位ベクトルである。
x方向、y方向、z方向の、それぞれ単位ベクトルを、i,j,k、とあらわせば、「外積」の定義にしたがい、sin0=0、sin(π/2）=1だから、
i×j=k , j×k=i , k×i=j
j×i=-k , k×j=-i , i×k=-j
i×i=0 , j×j=0 , k×k=0
このようなベクトル表記を用いると、xy直交座標上の微小な面積ΔS=ΔxΔy、下左図のような長方形の面積は、
ΔSk=Δxi×Δyj=ΔxΔyk
と書けることになるだろう。
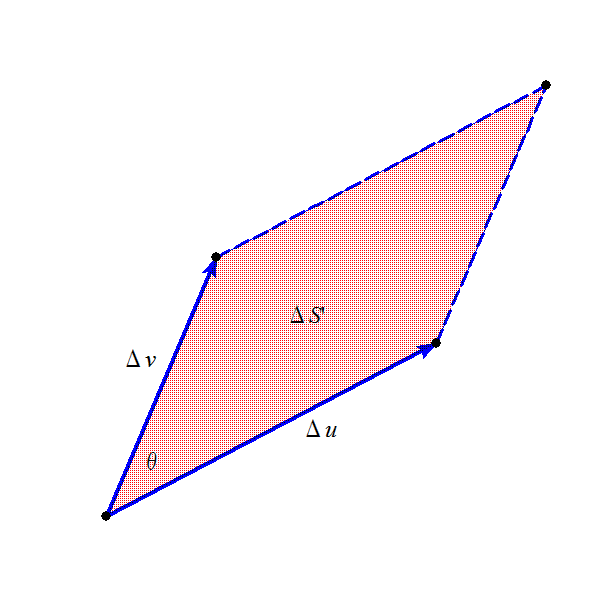
xy平面上の積分∬dxdyを、変数変換によって、uv座標に移し変え∬dudvとしたとき、
それぞれの座標系での微小面積ΔS=ΔxΔy、ΔS'=ΔuΔvの、関係を知りたい。
u,vはそれぞれ、x,yの関数、u=u(x,y)、v=v(x,y)であるから、
x→x+Δx、y→y+Δyの微小な変化に対応する、増分Δu、Δvは、
と書ける。偏微分
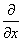は、x方向のみに着目した変化率、
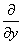は、y方向のみに着目した変化率、だからである。
このような表記、「全微分表示」が許されるか否か?には、既にして、偏微分可能性に関する条件が課されるのだが、それに関して私は上手に説明できない。私が理解していないからだが、・・・、そういう理由で、割愛する。
これをベクトルで表記すると、
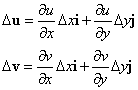
では、
uという方向をもち、Δuなる大きさをもったベクトルΔuと、
vという方向をもち、Δvなる大きさをもったベクトルΔvとを、
隣接する2辺とする平行四辺形の面積、ΔS'は、・・・、ΔuをΔvに向かって回転する際「右ねじ」の進行方向の単位ベクトルをnとすれば、
ΔS'n=Δu×Δv
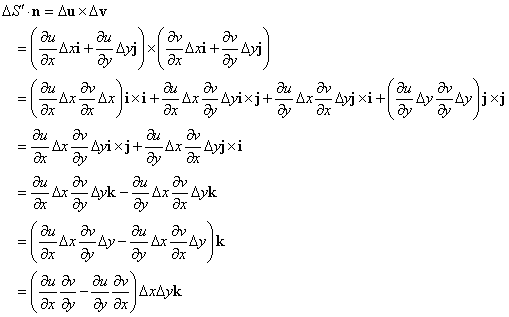
Δu,Δvはともにxy平面上のベクトルだったのだから、その外積の方向ベクトルnは、当然n=±kだったわけである。
ここで、ΔS=ΔxΔyだから、絶対値、ベクトルの大きさ、をとれば、
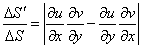
右辺には、何か「見覚え」（笑）はないか？、そう、
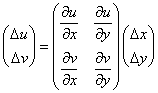
と表記したときの「行列式」なのである。こういうのを、「関数行列式(Jacobian)」と呼ぶのだそうである。
何がわかった(笑)のか?
∬dxdyを、変数変換によって、uv座標に移し変え∬dudvとするときには、
その微小面積の比率
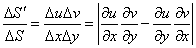を考慮する必要がある、ということが、わかった(笑)、のである。
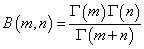
を示すのが目的であった。
Γ(m)Γ(n)=B(m,n)Γ(m+n)
として、左辺から右辺を導く。左辺、Γ(m)とΓ(n)の積分変数を、それぞれx,yと変えておいて、これを｢二重積分｣と見ることにする。
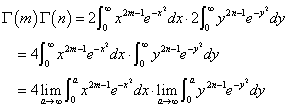
もともとは、x,yそれぞれを、独立に無限化するのであるが、いったん積分区間を0からaとしておいた上で、aを無限化してもよかろう?、というところまで、話した。
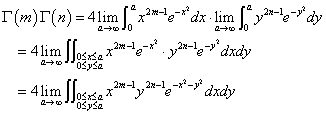
これを何とか、変数変換して、右辺の｢ベータ関数｣、
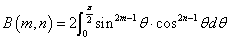
に近づけたい、似せたい、のである。左辺、Γ(m)Γ(n)のe｢ネイピア数｣の指数は、負号がついているものの、x2+y2の形をしていて、これを、
r2=x2+y2
とおいたらどうだろう?、(x,y)は、原点中心半径rの円周上の動点として、
x=rcosθ、y=rsinθ
と、まさに｢極座標｣表示できるではないか?
定積分の｢変数変換｣、つまり｢置換積分｣には、3つの作業手順があった。
- 被積分関数を、xの式からtの式に書き換える
- 積分変数の微小変化量、dxを、dtであらわす
- 積分区間を、xの範囲からtの範囲に書き換える
iiについてのお話が、前回の｢面積要素の倍率｣で、あとで述べる。
iiiは、0≦x≦aかつ、0≦y≦a、つまり原点中心、半径aの円の内部および周のうち、第1象限部分、というのだから、
0≦r≦aかつ、0≦θ≦π/2
でよいだろう。
では、｢面積要素の倍率｣、
xy座標上の微小面積ΔS、と、これをuv座標に変換したとき得られる新たな微小面積ΔS'との関係が、以下の「関数行列式Jacobian｣であらわされるのであった。
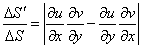
ここでは、
x=rcosθ、y=rsinθ
(x,y)が、(r,θ)の関数である、という形でこれを適用することになる。逆に、(r,θ)を(x,y)の関数と見ることもできないわけではないが、正の平方根、や逆三角関数、などが飛び出してきて、複雑になりそうだから、そうするのである。
だから、(x,y)座標上の微小面積ΔS'=ΔxΔy、(r,θ)座標上の微小面積ΔS=ΔrΔθの関係が、
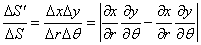
と、読み替えることになる。
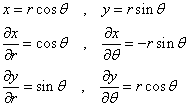
であるから、
すなわち、ΔxΔy=rΔrΔθであるから、ここでの｢二重積分｣の変数変換に当たっては、
∬f(x,y)dxdy=∬g(r,θ)・rdrdθ
としなければならないことが、わかったわけである。
早速はじめよう。
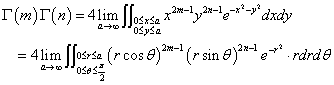
というわけである!、さらに変形を続ける。
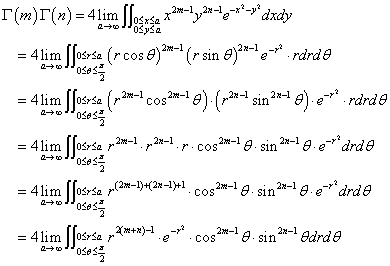
こうしてこの｢二重積分｣、ふたたび、rのみの積分と、θのみの積分との、積として、切り分けることができ、しかも、それらが、それぞれ、｢ガンマ関数｣型、｢ベータ関数型｣に対応していることに、・・・、もちろん、プロフェッショナルならば計画通り、として、しかし、凡人には、驚愕に値する(笑)事実として、気付かされるのである。
｢ガンマ関数｣、｢ベータ関数｣の変形された定義式は、
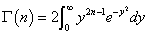
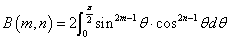
であったから、この式の右辺は、何度目をこすってみても(笑)、
Γ(m+n)と、B(m,n)の積にしか、見えないのである。
次回は、いよいよ(笑)、｢正規分布確率密度関数｣の紹介、になる。
あなたが(笑)、来春、大学に合格するかどうか?、とか、｢私｣の(笑)人生が幸福であったかどうか?、とか、マンボウがどうして4億個の卵を産まねばならないのか?、とか、・・・、そういった事柄を、まるで｢神｣の如く、規律しているかのような、この数式が、二項分布、世界には、「あること」と、「ないこと」、しかない、｢あること｣の確率は、コインの｢表｣やサイコロの｢6｣の如く、｢エルゴード性｣によって、つまり、特に区別する事情がな・い・、という｢否定文｣による立証によって等確率である、と｢確信｣できる、という、かなり｢雑｣としか言いようのない信憑構造に由来する単純な式の、｢極限｣の形なのである、という、またしても｢驚くべき｣(笑)事実の説明には、まだもっともっと、手の込んだ仕掛けが必要なのであるが、・・・、
それが、少なくとも｢確率｣を表示していること、平均値や分散が、その式を運用して過たず得られること、までは言えることになる。
それにしても、ここまでの大掛かりな｢ガンマ関数｣、｢ベータ関数｣の導入が、わずかにΓ(1/2)や、Γ(3/2)の計算にしか用いられないのは、解せないが、まぁ、｢世界｣は、そんな風な｢過剰｣、｢無駄｣に満ちているのだろう。
私が｢証明｣したいこと、死ぬまでにそれができないと、｢成仏｣できず、化けて出ざるを得なくなる(笑)のは、ただ一つ、
｢世界｣に、｢因果｣は、｢ない｣、こと。
私が｢不幸｣であったこと、「愚か｣であったこと、｢うまくいかなかった｣こと、それを受け容れることには、もはや、全然「やぶさか(吝)｣ではない。
ただ、それが、私の｢落ち度｣であった、という言論に対しては、いまだ、全力で(笑)、反駁しなければすまないのである。
私は、｢無罪｣である、証明したいのは、ただ、その一事である。
まずは、グラフをご覧に入れましょう。これが、正規分布N(m,σ2)、N(□,○)のNは「正規分布normal_distribution」、括弧書きの左側□には、平均値mean、だからm、右側○には分散、これはのちに説明するように標準偏差standard_deviation、σの2乗であるから、こう書く作法になっている。
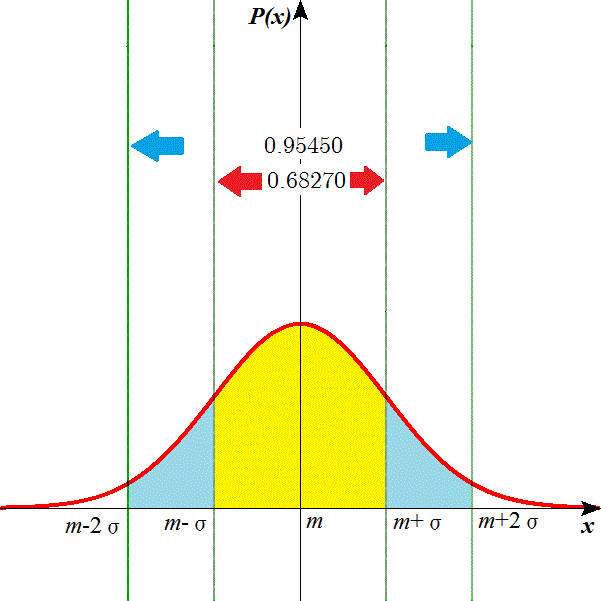
｢世界｣のあらゆる事柄は、この分布形に従うらしいのである。確かに、模擬テストの点数の分布であれ、ある国の国民の、所得構成であれ、・・・、みんな、こんな風な｢釣鐘型｣のヒストグラムになっている。｢中心極限定理｣なる不気味な理論があって、あ・ら・ゆ・る・分布は、標本数を十分大きく取ると、ことごとく、正規分布に収束する、というのである。
これは｢大数の法則｣や｢エルゴード性｣と同様、証明できる事柄ではなくて、事実として、受け容れざるを得ない｢経験則｣なのだ、という気がする。
のちに、いつになるかわからないが(笑)、二項分布の極限が正規分布である、なる理屈を、ノートにペンを走らせて何度繰り返しても合わない、三日くらいかかったか?、物凄く手の込んだやり方で、お目にかけることになるが、これも、何かを｢証明｣しているわけではなく、そう｢決めれば｣そうなるに決まっていることを、ただ、余りにも複雑になってしまったから、一目瞭然とはいかない、｢確認｣の手続きに過ぎないものが、何か新たな｢発見｣をもたらしているかの如き｢錯覚｣なのではないか?、と、素人ながらに、思う。
改めてグラフを眺めてみましょう。なんとも含蓄の深いグラフなのです。ちなみに、
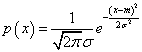
などというとんでもない数式を入力するだけで、さらりさらりとグラフを描いてくれるソフトウェアは、「grapes」という名称で、確か大阪教育大学の先生が開発されたものを、講談社ブルーバックスの付録でもよいが、今ならインターネット上で無料で入手できるものだ。
mは、平均値である。σ、標準偏差は、｢分散｣の正の平方根、分散は、偏差、すなわち平均値との差の2乗の平均値、と定義される。集団の中には、平均値から上に外れているものと、下に外れているものが、必ず(笑)存在するから、・・・、｢偏差｣をそのまま足したら、それは正負を帯びた数だから、必ず合計0になる。分布の｢広がり｣を評価するには、その｢絶対値｣を加算する必要があるが、｢絶対値｣という｢手続き｣は、実はややこしい、それがプラスであるかマイナスであるかあらかじめ「知らな」ければ判断できないのである、そこで一律｢偏差｣を2乗する、という便法をとるのである。
こうして｢分散｣、各データの平均値との差(偏差)、の2乗を加算し、標本数で割り算した、｢偏差｣の2乗の、平均値、は、それが大きければ分布は、下の左の図のように、ピークが低く裾野の広い｢なだらかな｣形、それが小さければ、下の右の図のように、逆にピークが高く裾野の狭い｢シャープな｣形、と判定することができる。
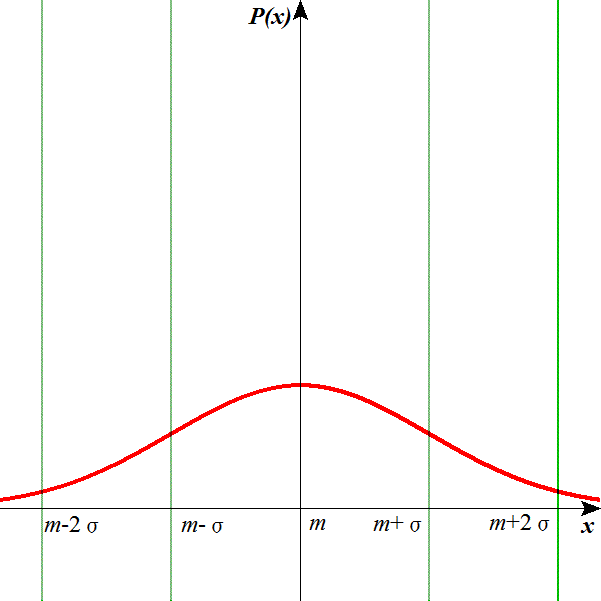
ところが困ったことに、｢分散｣の｢次元｣は、たとえばデータがテストの点数なら、その計算方法から伺われるように「点数2」というもので、これでは｢意味｣がわからない。100点満点のテストで、分散を計算してみると、400とか700とか、それで｢へー、大きいですね｣などといえるのはプロフェッショナルのみである。｢分散｣の正の平方根をとると、これが再び｢点数｣の次元だから、グラフの横軸にプロットできるようになるのである。これがσ、標準偏差。横軸上のσの幅を一律に取れば、｢なだらかな｣分布も、｢シャープな｣分布も、ほぼ同じ形に重ね合わせることができる。
その｢極限｣的な理想形が、上のグラフなのである。平均値のまわりのプラスマイナス1σのレンジに、m-σ≦x≦m+σに、理論上0.68270、約70パーセントのデータがおさまっている。これが、｢いや、普・通・、そうするでしょう?｣なる、ときとして暴力的な、｢普通｣なる用語に対応するといってもいいだろう(笑)。
さらに、平均値のまわりのプラスマイナス2σのレンジに、m-2σ≦x≦m+2σに、なると、0.95450、約95パーセントであり、これが、世間に流布する｢多数派｣なる用語の、通約的な意味を構成する。
何か新製品を購入したのに、不良品だった、みたいなことが繰り返し起ったら、・・・、前世の因縁、先祖の祟り、とは言わずとも、嗚呼、私ってよほど運が悪く｢生まれついて｣いるのね?、と、｢因果｣的に、落ち込んでしまいます。メランコリー親和型の人間は(笑)特にそうです。
｢ウォター・プルーフ｣のデジタル・カメラが、海にもっていった一日目に壊れたことが、2度、ありました。保証期間内だから無料で取り替えてもらえたけど、ディスカウント家電量販店の店員さんは、忙しいからだろう、ちくりちくりと嫌味を言うし、精神的には、ずいぶん「傷つき」ました(笑)。
そんなことが、そうしばしば起る事態ではないことを、私たちは「経験上｣知っているのです。そうでなければ、安定した生活を営むことができないからです。だから、家電製品のみならず、工場生産の製品の品質管理には、ちゃんと｢統計学｣が利用されていて、不良品が市場に出る確率が、平均値プラスマイナス2σの外側、すなわち5パーセント未満であるようにするには、どの程度の規模の標本(サンプル)に対して抽出検査をしなければならないかを、｢正規分布｣の数表から、算出しています。95パーセント信頼区間、などと世に言うのは、これです。
｢偏差値｣という用語は、｢統計学｣的装いを帯びているが、受験産業が捏造したものだろう、と思っている。私が受験生だった頃は、模擬テスト、そもそも、そんなもの、一年に2回くらいしかなかった(笑)けれど、の｢データ｣には、平均値・・・、標準偏差・・・、などとそっけなく記載されているだけだった筈だ。進路指導の先生(笑)が、それでは｢わからない｣かもしれない親切心から、この正規分布グラフ、もちろん理論上は、マイナス無限大からプラス無限大を定義域とする、を、100点満点のテストに｢なぞらえて｣、平均mを一律50点、標準偏差σを一律10点、と、もちろん何の根拠もなく(笑)読み替えて、算出した。
｢偏差値｣40〜60が、m±1σで、68パーセント、｢偏差値｣30〜70が、m±2σで、95パーセント、というわけだ。
「この生徒、模試の偏差値100超えてるんですけど、どういう意味ですか?」と、かつての職場の進路指導担当アドバイザーさんに、質問されたことがある。その生徒が｢優秀｣であることは疑いないから、褒めてあげて差し支えないが(笑)、これはm+5σを超えているわけで、手元の数理統計学の教科書の数表でも計算不能として省略されている(笑)、それほど｢優秀だ｣というべきではなく、そもそも、その模試の標本数が、統計学的検討に値するほど、｢エルゴード性｣、｢大数の法則｣、｢中心極限定理｣、等々をもちだすほどの、｢大きさ｣を有していないことの｢戯画｣、なのである。
世に｢5段階評価｣と呼ばれているものも、この｢正規分布｣を基準にしている。わずか一クラス50人そこそこのヒストグラムが、｢正規分布｣に似ていなければならない(笑)理由はないにもかかわらず、・・・。
平均値プラスマイナス0.5標準偏差、m-0.5σ≦x≦m+0.5σが、｢3｣、手元の正規分布表によれば、これは0.38292、全体の38パーセント、
その外側、平均値プラスマイナス1.5標準偏差、までのレンジ、に｢2｣と｢4｣が振り分けられる。それぞれ0.24173、全体の24パーセントずつ。
m-1.5σ≦x≦m-0.5σが、｢2｣、で、m+0.5σ≦x≦m+1.5σが、｢4｣。
そのさらに外側、が、｢1｣と｢5｣、それぞれ0.0681、全体の約7パーセントずつ。
x≦m-1.5σが、｢1｣、で、m+1.5σ≦xが、｢5｣。
このパーセンテージを、たとえば50人に割り当て、｢1｣3人、｢2｣12人、｢3｣20人、｢4｣12人、｢5｣3人としただけの(笑)ことである。
小学生だった私は(笑)、国語、算数、理科、社会は｢5｣だったが、体育、音楽、美術は｢1｣だった。余程｢普通｣がお嫌いなようである。今も(笑)、たとえば、それ以外に誇るところのない(笑)｢学歴｣、などでは、m+2σを超えているかも知れないが、この春会社を馘首になる前も既に、なってからはもちろん(笑)、年間所得はm-2σ未満の筈だ(笑)。
この国の人口がどれだけなのかよく知らないのだが、仮に1億とすれば、m-2σ未満の｢下流｣は、m+2σを超える｢勝ち組・セレブリティー｣(笑)と、全く同じ比率(笑)、0.0225、2.25パーセント、人数にすれば、二百二十五万人、「も」いるのだ、と思えば、心強い(笑)。
当地に来てから15年、特に数学が好きなわけでも得意なわけでもないのに、それしか能がないから、｢数学の先生｣をしていたわけだが、いつも｢すわりの悪い｣思いをしていたのは、「模試の結果、○○大学の合格可能性、C判定、だったんすけど、チャレンジしてみるべきでしょうか?｣といった質問に、私は答えることができないのである(笑)。一応、数学を｢専門｣とする者としての｢良心｣(笑)が、許さないのである。それは｢統計学｣の｢誤用｣だ、と思っているのである。思うに、｢統計学｣は、ある種のバクテリアや、キイロショウジョウバエや、｢国民｣や、｢消費者｣や、模擬テストの受験者でもかまわない、そのような集団に対して、その｢外側｣から、その集団を｢管理可能｣と見做す、いわば｢神の眼差し｣で、語られる物言いなのである。
｢神の眼差し｣は、対象の｢個性｣を没却する。遺伝の実験に用いられる大量のキイロショウジョウバエに、一匹一匹、うちの猫たちのように(笑)、｢名前を付ける｣ことは、おそらく、できない。｢名付けることができない｣ことを以て、順列・組み合わせ・確率、と言った｢数え上げ数学｣理論は、｢区別がつかない｣と称しているのである。
あなたは、｢区別のつかない赤玉｣、となることではじめて、模擬テスト会社のデータに記載された。本当は、泣きもすれば笑いもする(笑)、・・・、
花は花として、涙も流す、人は人として、笑いもできる、・・・、唐突ですが(笑)、喜納昌吉｢花｣、でございます、
名付けうる｢赤玉｣であったのに、そのすべての個性を没却することではじめて、｢正規分布｣グラフを構成する、一標本、となった。にもかかわらず、今になって、その｢正規分布｣グラフを指差しながら、
｢私は・ここに・いる｣、と言うのは、｢統計学｣の守備範囲を、超えている、と、思うのだ。
私自身が、そんなに｢統計学｣を理解していないから、自信はない、だから、今になって｢勉強｣しているわけだが(笑)、これも｢死ぬまでに｣(笑)片付けたい課題ではある。
マンボウが4億個の卵を生み、そのうちの1個のみが生き延びるとしよう。私たちは、誰かが、マンボウの卵を一つ一つ追跡する詳細な研究を行ったからこそ、それを知っている。知った上で、マンボウの卵が生き延びる確率は、4億分の一だ、と言っている。
｢確率｣と言うのは、｢知っている｣か「知らない｣かによって、値が変る。後攻めチームが勝っている野球の試合、9回裏はやらない約束だが、双方合意で、やってもいいのである。やる気を失った守備陣を尻目に、ぼかすか打ち込んであと10点くらい取っても、いいのである。この段階で、たとえば野球賭博で(笑)、先攻めチームに賭ける人はいない。既に生じてしまったことの、｢確率｣は、1、決して生じることのなかったことの、｢確率｣は、0、つい数分前、9回表の段階では、｢確率｣は、0と1との間の、不確定な数値を取っていたにもかかわらず、・・・、この0と1と言う｢凡庸な｣(笑)数値への急速な｢収束｣は、ひとえに、｢私たち｣が、賭博参加者が、結果を｢知る｣ことによって生じた。
箱の中に手を突っ込んで、三角形に折りたたまれた「くじ」を引く場合でもいい。あなたが｢透視能力｣を有していたとしよう。これがもはや｢くじ｣ではないのは、あなたは、｢当たり｣であることを｢知って｣、｢当たり｣を引く、確率1、｢はずれ｣であることを｢知って｣、｢はずれ｣を引く、確率0、に既に収束していて、だからきっと透視能力者は｢わくわく｣できない。｢わくわく｣できるのは、ひとえに｢知らない｣からこそ、当たる確率が、0と1との間のどれかの値でありうるからなのだ。
四億個のマンボウの卵のひとつになったと想像してみよう。「あなた」にとって事態は、｢生き延びれる｣か｢生き延びれない｣か、のどちらかである。どちらもの可能性に、特に異なる理由がなければ、｢エルゴード性｣により、それは等確率それぞれ1／2、｢あなた｣が｢生き延びる｣可能性は1／2である。
｢観測者｣である｢私｣は、個々のマンボウの卵が、｢生き延びる｣確率が、四億分の1であることを｢知って｣いる。だから、｢あなた｣の推論の誤りを、指摘してあげることもできる。だが、｢私｣は、「あなた」がほかならぬ｢生き延びれる｣たった一個の卵であるかどうか?、についての問い合わせには、決・し・て・、答えることができない。｢観測者｣には、四億個の卵を区別する、つまり、｢名付ける｣、ことができないからである。
そして、もうひとつ、ひとつのマンボウの卵である｢あなた｣にとって、｢生き延びる｣確率が1／2であるか四億分の一であるかを｢知る｣ことは、その後の行動の選択に、なんら影響を及ぼさないのである。
｢生きる｣ことに｢理由｣はないので(笑)、ただ、今生きているから、次の、微小時間経過後も、生きる、のである。BASICで書けば(笑)、
do while (条件文)
・・・
enddo
の｢条件文｣が、｢続いているなら、続けろ｣、みたいな｢トートロジー｣になっているのである。この無限ループを切断するのは、｢外部｣の要因、電池がなくなった、とか、コンピュータが壊れた、でしかない。キュルケゴールが(唐突ですが・笑)、｢人間は死を想念に取り込むことができないから、漠然とした不安を引き入れた｣と言うのは、多分(笑)、その意味だ。
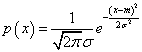
この式の変数xの定義域は｢実数｣、-∞から、+∞の稠密につながったすべての値をとりうる。そのうちのある特定のxの値に対応する確率が、p(x)と名付けられているのである。
ここでは、3項目についての確認をしたい。
- この式は、確率分布をあらわすというが、そうならば、すべての場合の確率を合計すれば、｢1｣になっていなければならない筈だ。
- N(m,σ2)、つまり、平均値m、分散σ2、というが、まず、平均値は本当に(笑)mなのか？
- 同じく、分散は、本当に、σ2なのか？
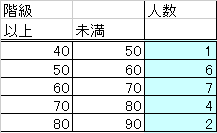
確率変数が、サイコロの目のように、飛び飛びの値、離散変数でなく、連続変数である、というのは実はかなり想像しがたい。たとえば人間の｢体重｣などという値は、小数点以下をどんどん細かくとれば、｢理念｣型としては(笑)連続変数であるが、実際上の処理としては、それを階級に区分して、下の度数分布表、ヒストグラムに見るように、たとえば50キログラム以上、60キログラム未満の6人のサンプルは、全員ことごとくその｢階級値｣、階級の両端の平均値55キログラムという、離散変数、だった、と見做して、処理するのである。
この例を手掛かりに、考えてみよう。
- まず、すべての場合の数の合計が｢1｣であるとは、この例で｢確率｣を云々するには違和感(笑)もあるが、この20人の誰かを指差して、その人が、60キログラム以上70キログラム未満の階級に属する｢確率｣は、7/20である、といってもいいだろう?
すべての階級についてその足し算をすれば｢1｣になるのは利の当然で、人数の合計を人数の合計で割ったら｢1｣だ、といっているに等しい。
1/20+6/20+7/20+4/20+2/20=1
これを連続変数化すると、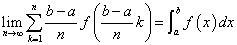
これは｢区分求積法｣と呼ばれているもので、定積分の定義そのものなのだが、滑らかな曲線下の面積を計算するのに、まず積分区間をn等分してぎざぎざの長方形の面積の合計を算出し、しかるのち、nを無限化すればよいではないか?、といっている。
平たく言うと、ならば最初からそう言え!、｢細かい掛け算の足し算｣が、｢積分｣である。ここでは何も掛けていないではないか?、という疑問が生じるが、それは、各階級を等価として、1を掛けているのだ、
1×1/20+1×6/20+1×7/20+1×4/20+1×2/20=1
と｢思えば｣、よい。しからば、連続変数化されたすべての場合の確率の和は、
∫1×p(x)dx
と言ってよかろう。
ちなみに、これは、正規分布曲線の曲線下の面積が、つねに1だと言っている。
ピークが低くて裾野が広くても、ピークが高くて裾野が狭くても、-∞から+∞までの、曲線下の面積は、つねに1だと言っている。 - 期待値、20人の誰かを指差して、その人の体重が、どのぐらいであることが｢期待｣されるか?、というのは、かなり苦しい言い回しになるが、それはおそらく、確率という概念が、｢未来｣の、｢未知｣の事柄に関わらざるを得ないからで、それを体重などという、測ればそれまで(笑)、｢既知｣の事柄を例に引くからわかりにくいだけで、｢未来｣への｢期待｣を、既に起ってしまった｢過去｣に引き直せば｢平均値｣という平凡なものになる、ということであろうか?
体重の｢平均値｣を導く式は、
45×1/20+55×6/20+65×7/20+75×4/20+85×2/20
だから、これを、連続変数化すれば、先ほどの1の代わりに各階級値を掛けているのであるから、
E(x)=∫x×p(x)dx
となるだろう。 - 分散V(x)は、｢偏差の2乗の平均値｣であった。ところが、エクセル、などという便利なもののない時代、紙と鉛筆で、電卓を用いてさえ、この定義式では、事実上、計算不可能なのである。なぜなら、通常、平均値がさっぱりとした整数値になることは期待できない、小数点以下長々と続く数だった場合、各データの偏差も同様、そんな長ったらしい数になる、ましてやそれを2乗すれば、小数点以下の桁数はなお延びる、・・・、
そこで、こんな便利な変換式がある。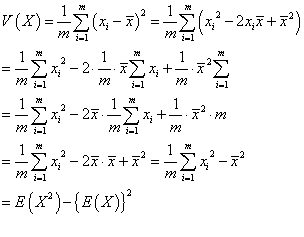
つまり、分散は、｢2乗の平均-平均の2乗｣なのであった。
「2乗の平均」は、先ほどの体重の例に戻れば、
452×1/20+552×6/20+652×7/20+752×4/20+852×2/20
だから、同じく連続変数化するには、
E(x2)=∫x2×p(x)dx
となるだろう。
準備が整った。では、始める。
- すべての場合の確率の和が1であること、
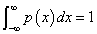
を示したい。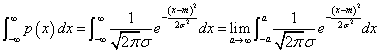
以下のような変数変換(置換積分)を行う。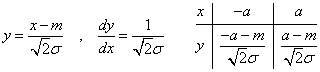
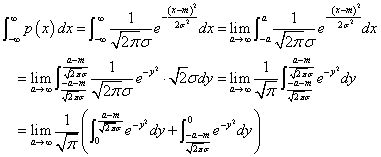
第2項に以下のような変数変換を行う。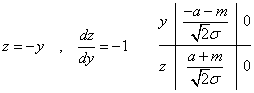
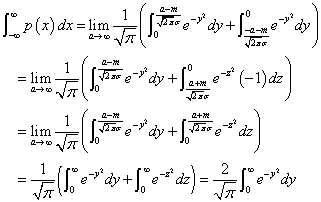
ここでやっと話がつながるのである。｢ガンマ関数｣は、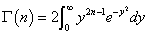
であった。どうやら、n=1/2のときの｢ガンマ関数｣の式が、右辺に現れているらしい。
｢ベータ関数｣は、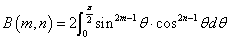
｢ガンマ関数｣と｢ベータ関数｣の関係は、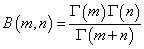
であったから、前にも一度紹介したが、次のような手順でΓ(1/2)を得ることができる。、というか、それ以外の方法では計算することが、できない。
自然数nに対する｢ガンマ関数｣は、Γ(n)=(n-1)!であったから、長々とお話したように(笑)、Γ(1)=0!=1で、
したがって、
よって、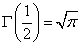 
元の式に戻ると、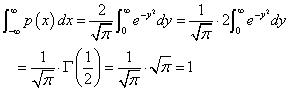
これが証明すべきことであった(笑)。 - 期待値E(x)が、本当に(笑)、mであること、すなわち、
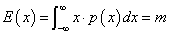
を示したい。
上と同じ、以下のような変数変換(置換積分)を行う。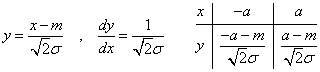
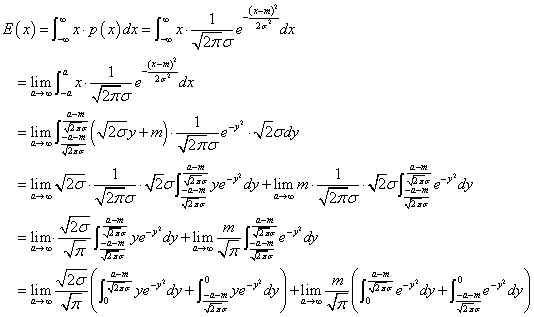
それぞれの括弧の第2項に、同じく以下のような変数変換を行う。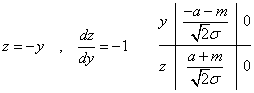
これまた(笑)、これこそが、証明すべきことであった! - 分散V(x)が、本当に(笑)、σ2であること、を示したい。
V(x)=E(x2)-{E(x)}2であったから、そして、E(x)=mであることはもうわかっているから、E(x2)を計算したい。
上と同じ、以下のような変数変換(置換積分)を行う。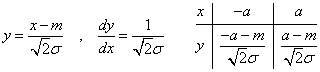
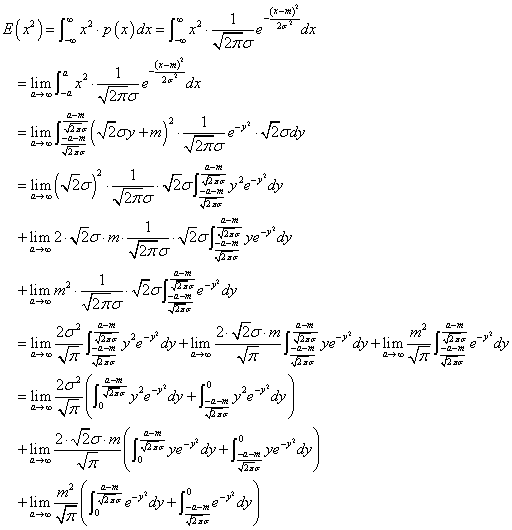
それぞれの括弧の第2項に、同じく以下のような変数変換を行う。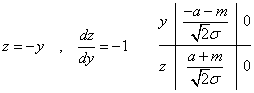
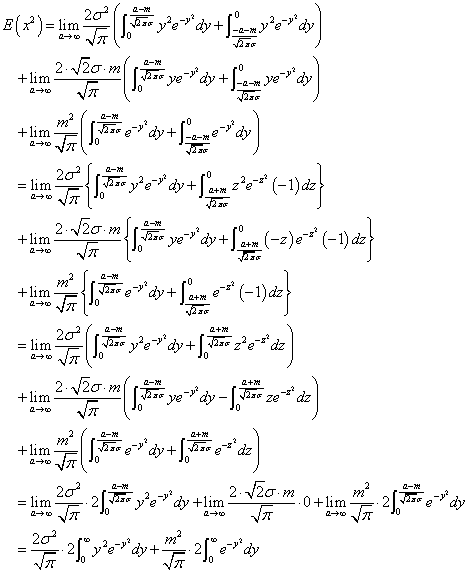
ここでふたたび、｢ガンマ関数｣が、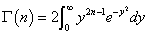
であったことを思い出していただくと、第1項は、2n-1=2、すなわちn=3/2、第2項は既にやったようにn=1/2の｢ガンマ関数｣にあたることがわかる。
さらに、｢ガンマ関数｣に関する漸化式、
Γ(n)=(n-1)Γ(n-1)
を想起すれば、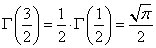
こうして、たしかに、
V(x)=E(x2)-{E(x)}2=(σ+m2)-m2=σ
を得ることができた(笑)。
- すべての場合の確率の和、すなわち｢1｣は、
1=∫1×p(x)dx - 「期待値」は、
E(x)=∫x×p(x)dx - 分散の算出に必要な、「2乗の期待値」は、
E(x2)=∫x2×p(x)dx
次のような関数を定義してみると、
φ(θ)=∫eθxp(x)dx
- まず、
φ(0)=∫1・p(x)dx - これをθで1階微分して、
φ(1)(θ)=∫xeθxp(x)dx
したがって、
φ(1)(0)=∫x・p(x)dx - さらにθで微分して、
φ(2)(θ)=∫x2eθxp(x)dx
したがって、
φ(2)(0)=∫x2・p(x)dx - 一般化して、θでk階微分したとすると、
φ(k)(θ)=∫xkeθxp(x)dx
したがって、
φ(k)(0)=∫xk・p(x)dx
これをもって、「0に関する第k積率」と称し、そのような｢積率｣を生み出すものとして、
φ(θ)=∫eθxp(x)dx
を、｢積率母関数｣と呼ぶ。
k=0のとき、これは、すべての場合の確率の和、に当たるわけだが、これも、たしかに、定数x0=1についての｢期待値｣E(x0)と呼べなくはないだろう。
ところで、ここで、上のような変形が許されるのは、
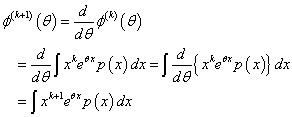
というように、θに関する微分と、xに関する積分が｢交換可能｣であることが前提となっていて、いかなる条件の下に、そのようなことが許されるのか?、を議論しなければならないはずなのだが、残念ながら(笑)それは私の手に余るので、そのようなことが可能であったとして、・・・、と話を進める。
xが連続変数でなく、x1,x2,・・・,xi,・・・,と、飛び飛びの値をとる離散変数であった場合はどうであろう?
P(X=xi)=piと書けば、
- すべての場合の確率の和、すなわち｢1｣は、
1=Σ(1×pi) - 「期待値」は、
E(x)=Σ(xi×pi) - 「2乗の期待値」は、
E(x2)=Σ(xi2×pi)
φ(θ)=Σ(eθxipi)
あれ？、「html(Hyper_Text_Markup_Language)」で書くと｢上付き文字｣の中の｢下付き文字｣が基準と同じ高さになってしまって訳がわからない!、｢数式エディター｣で書き直すと、
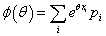
を、採用すれば、
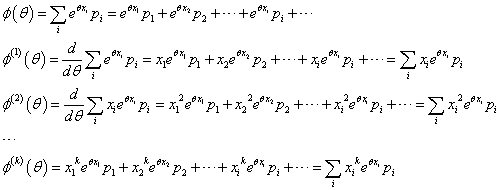
0に関する第k積率φ(k)(0)は、
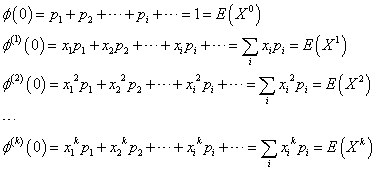
となり、上3行がそれぞれ、「すべての場合の確率の和」、「期待値」、そして、「2乗の期待値」、と、なっている。
ここでも、このような変形が可能なのは、項別微分可能である、とか何とか言わなければならないはずなのだが(笑)、確信がないので(笑)、不問に付す、というか、お茶を濁しておく。
こうして、｢積率母関数｣なる概念を導入することで、「期待値」や「分散」の計算が、それぞれ｢0に関する第1積率｣、｢0に関する第2積率｣を求め、・・・、などというように、形式的な｢呼び名｣を以て引用することで、いわば｢機械化｣できるのである。これが、｢名付ける｣ことのメリットであろう。
話は、正規分布確率密度関数から始まったのだが、正規分布については、積率母関数を導入したとしても、その計算には、やはり、ガンマ関数だのベータ関数だのの議論が必要であることには変わりなく、余り有り難味がない。｢有り難味｣を実感するために(笑)、次回は、まず、離散変数型として二項分布、次に、そのある種の極限化によって連続変数化されたポアッソン分布について、積率母関数を用いた計算を実見してみる。
では、このような試行を｢独立｣に、n回繰り返したとき、そのうちi回のみ、その「あること」が生じる確率は、
P(X=i)=nCipi(1-p)n-i
このような数式で表示される確率分布を、二項分布Binomial_Distribution、B(n,p)と称するのであった。
積率母関数として、
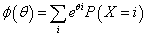
を採用すれば、
ここに「二項定理｣Binomial_Theorem
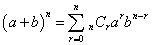
を適用すれば、
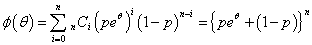
これを順次θで微分して、
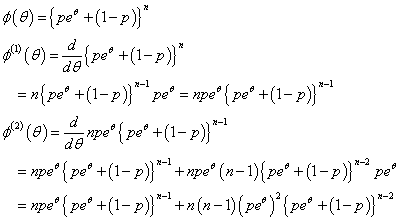
然らば、0に関する第0積率、第1積率、第2積率は、
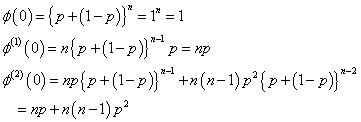
これらがそれぞれ、E(X0)、E(X1)、E(X2)にあたるわけで、
ならば、分散は、
V(X)=E(X2)-{E(X)}2=np+n(n-1)p2-n2p2=np(1-p)
となるのである。なるほど、以前紹介したように、直接求めるよりは、簡便であるとはいえる。
二項分布の極限だ、という言い方がなされるが、アプローチは二通りあるように思われる。まずは、二項分布の計算が困難であるときに、近似する言わば「便法」として、・・・。
ある生き物が、ある時間単位に、「生き延びれない」事態に立ち至る確率が1/1000だったとしよう。一万時間単位、「生き延びる」確率は如何程であろうか?
「人間」で考えるなら、その1時間単位を一日、と思えば、一万日は、365で割ると、約27年、幼年期と老年期は、それぞれ「死に易い」であろうから、それを除外した青年期の27年、日々「死ぬ」確率が1/1000のさなかを生き抜いているのだ、という想定は、そう非現実的でもないと思う。
一回の試行において、「あること」が「生じる」確率が一定値p、ここでは1/1000であるとき、n回、ここでは一万、の試行中その「あること」がi回「生じる」確率は、二項分布B(n,p)であらわされるのであった。
P(X=i)=nCipi(1-p)n-i
生き物は、一度死んだらそれまでなので、2回以上「生ずる」話はナンセンスであるが、後攻めチームが勝っている野球の試合の9回裏、当たりくじが出尽くしたあとのくじ引き、と同様、生き返ってまた死ぬ、と考えても、かまわない。ここでは、10000時間単位「生き延びる」確率を知りたいので、10000回試行したが、「あること」がただ一度も生じなかった確率、
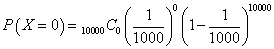
を計算すべきことになる。10000C0=1、(1/1000)0=1だから、0.999の一万乗の計算、というわけである。この計算が困難だから、ポアッソン分布で近似する、というのである。式の導出は後の話として、ここでは、ポアッソン分布P(m)の式が次のように得られた、としてその近似の度合いを確かめてみたい。
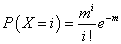
ここにmは、平均値、である。お気づきのように、無論、私がやっと気づいた（笑）のであるが、ポアッソン分布の式には、どこにもn回という試行回数が含まれていない。無限化されているのである。だから、nがとても大きいとき、よりよい近似になるといわれる。
二項分布の平均値は、m=npであったから、ここでは、m=10000×(1/1000)=10を採用すると、
を計算することになる。0!=1となる「理由」は、すでにくどくどとお話したとおり（笑）である。
0.999を一万回かけるのと、ネイピア数の逆数を十回かけるのと、どちらが「楽」か?、と問われても困惑するが（笑）、一応、後者に軍配が挙がる、ということで納得しよう。
どちらも「エクセル」で計算できる範囲なので、私は既に答えを「知っている」（笑）のだが、ここでは、敢えて、て計算で概算してみたい。ネイピア数が約2.7であること、2と3の常用対数がそれぞれ約0.30、0.48として。
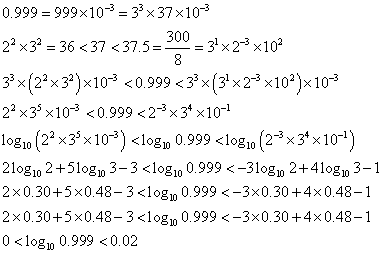
という愚かな結果、真数が1より小さい対数が正になるわけないので、に陥ったのは近似が甘すぎて誤差が大きくなり過ぎたのだな。
ネイピア数の逆数の10乗の方は、うまくいった。
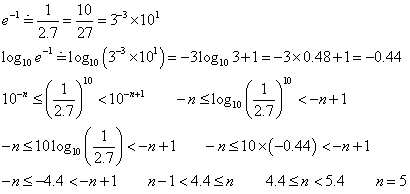
というわけでこの数は、小数点以下第5位に初めて0でない数字が表れるような数、であることがわかったのである。
「エクセル」による正解は、0.99910000=4.52×10-5、e-10=4.54×10-5
であるから、概算のもくろみは水泡に帰し、オチのない話（笑）になったが、どちらも、めちゃめちゃ小さい、としか言いようのない数であるが、確かに二項分布がポアッソン分布でよく近似出来ていることは、わかった、ということで。
私たちの多くが27年間、「平然」と生きて来たのは、したがって、奇跡に近いのだ、と納得している場合ではなくて、日々の危険の見積もり1/1000がそれでも、大き過ぎた、ということになるかな。そんなこともない気もする、やはり「生きている」ことは奇跡に近い、と思うんだけどね（笑）。
ポアッソンは人名なんだろうか?、確かフランス語で、poisonなら英語と同じ「毒」、poissonなら「魚」だったおぼろげな記憶がある。手許にフランス語の辞書ないから、いい加減な薀蓄・・・。
について、いずれもピークが三つ並ぶが、左から順にp=0.1、p=0.2、p=0.5、に対応する。
赤色が二項分布、青色がポアッソン分布。
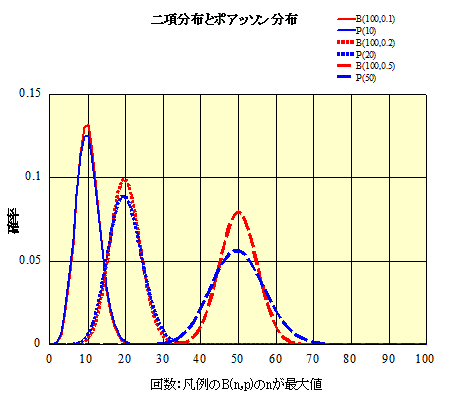
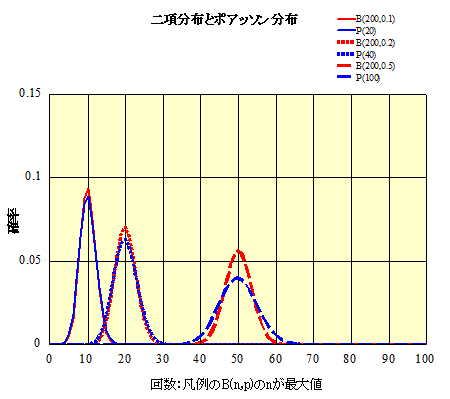
二項分布をポアッソン分布で近似する、という観点からは、ポアッソン分布の方が、いずれの場合も、ピークが低めのなだらかなグラフ、pが小さいほど、近似の精度はよさそうである。nが大きいほどまた精度がよくなる理屈ではあるが、n=200を超えると計算できないみたいだから、余りはっきりしたことはいえない。
二項分布B(n,p)、1回の試行で「あること」が「生ずる」確率がpである試行をn回繰り返したとき、そのうちi回、その「あること」が「生じる」確率、
P(X=i)=nCipi(1-p)n-i
これを、np=mを一定値として固定した上、nを限りなく大きくものがポアッソン分布であるといわれる。もちろん、これにともないpは、限りなく小さくなる道理だ。
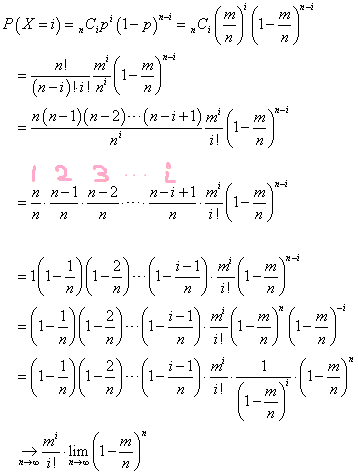
pを消去し、ちょいと（笑）変形して、nを限りなく大きくすると、「1引く無限大分の1の無限大乗」という不定形部分を残し、何とか解決する。と、「事も無げ」に語っているが、理解するのに最初は半日くらいかかった（笑）筈だ。残った部分がネイピア数の逆数に収束すれば、目標達成、である。これは、次のように「説明」できる。「証明」でなく「説明」なのは、まず、ネイピア数の定義を「受け容れた」上での議論だからだ。
f(x)=logaxという関数の導関数を求めたい。
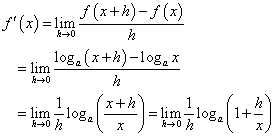
ここで、y=h/xなる変数変換を施すと、h→0のとき、y→0だから、
もし、
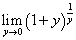が、有限確定値に収束す・る・な・ら・、その収束値をe、ネイピア数、と名付け、
となり、高校の教科書にも出ている（笑）微分法の「公式」になるわけである。
- そもそも、本当に（笑）、収束するのか?
- 収束するなら、その収束値はいかほどなのか?
- 「級数展開」を用いて計算すると、どうやら、その収束値は、2.7某、という、いつまでたっても循環しない小数、どうやら無理数であるらしい、ということが知られる、
ただここでは、それらが既に「わかった」事として、ポアッソン分布の式を導くことに集中することにする。
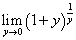=eに対して、z=1/yなる変数変換を施す。y→0に対して、z→±∞
したがって、
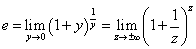
を求めたいのであった。x=-n/mなる変数変換。mは定数と固定されていたから、n→∞なら、x→-∞、である。よって、
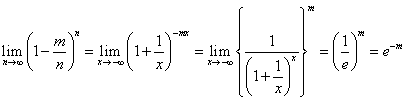
こうして、ポアッソン分布P(m)、
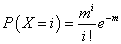
が得られた。
議論の「隙間」は、順次、埋めていける、筈（笑）、である。
一個の「何か」が、「この」区画に落ちる確率p=b/aとして、これがn回繰り返されるのだから、二項分布B(n,b/a)を適用することになるだろう?
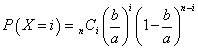
そこで、単位長さあたりに「何か」が「降る」確率を一定とみなして、たとえば、k=n/a、とすれば、これは、単位長さあたりk個が「降る」としている、それを一定とした上で、aは実は無限の長さなのだ、といえば、そうなれば「降って」来る総数nも無限とならざるを得ず、・・・、このような「無限化」の彼方に現れる確率分布をもって、ポアッソン分布と呼ぶのだ、というわけなのである。
aを消去して、nを無限化すべく、前回と同様の変形を施せば、
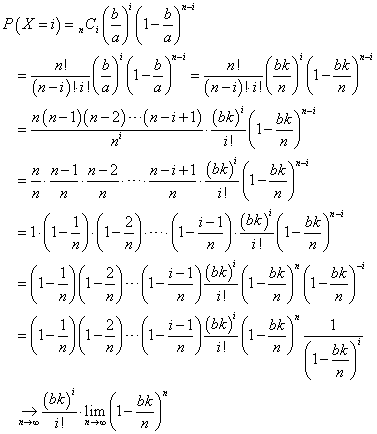
ほら、同じ形になった!、kは一定といっただろ?、それに、bという「長さ」も一定と見ていいだろ?、だから、bkも一定じゃない?、だったら、それmっておいたらいいじゃない、と、矢継ぎ早に（笑）攻め立てられると、頭の悪いものは、当惑してしまいます。
もちろん、bk=mとおけば、ネイピア数の定義にしたがい、
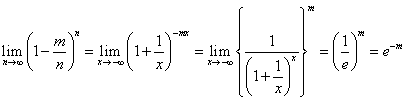
となって、
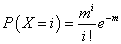
ほら、ポアッソン分布になったじゃないか?、そのとおりであるが、一体このmとは、なんなのだ?
のちに、積率母関数を定義したのち、計算してみると、なんとこのm、ポアッソン分布の平均、お・よ・び・、分散であることが知られるのだが、それを持ちだすのは「本末転倒」に思えるから、しばしmの「意味」について、考える。
長さaの線分に、均等に何かが「降る」という想定は、そもそも無理が多い、と思う。ふたつの壁に区切られた中庭に雨が降る場合なら、風向きによって、一方の端は雨宿りができるのに、他方の端では、壁からの跳ね返りもあってなお濡れやすい、つまり、「境界」は「異常」であることが多い。
子猫の母親、ぷにおぷにこ♪、もそれはちゃんと知っていて、だから、台風8号「ノグリー」到来前夜、壁に近い方の（!）犬小屋に「引越し」したのだ。「ノグリー」は沖縄本島の西側を北上した、低気圧には中心に向かって外から風が吹き込む、つまり、当地では、東から西への風が強くなる、うちのベランダは、東側に建物があって、東風を遮ることができる、まことに、建物近くの壁際は、濡れないのである、そんな「推論」を、ぷにおぷにこ♪、がしたかどうかは知らない、ただ、現に、「彼女」の選択は、「正し」かったのである。
前にもお話したが、集合を表記する「ベン(Venn)図」は、重宝なものだが、全体集合を長方形で描いてしまうと、無限集合の場合、その四囲があたかも「境界」であって、そこがどうなっているのか?、が、やや、いかがわしい（笑）。平面に長方形を描くと、そこに「内部」と「外部」の、区別ができてしまうからだ。「無限」を馴致する（笑）、「リーマン球面」がここでも役に立つ。
表面積aの球面上に、均等に何かが「降る」、一つ一つの何かが「降る」確率は、球面上のどこでも同じ、それがn回繰り返されたとき、球面上のある区画、面積bのエリアに、iこの何かが「降る」確率如何?、と読み替える。
そうするとたちまち、この球面をあたかも地球、その表面上の区画を「国」とか「地域」とかに当てはめるアナロジーが成立しがちだが、それは、ポリティカリー・インコレクト（笑）、だから採用できない、ということを強調しておかねばならない。何かが「降って」来る、というとき、「あなた」は、ミサイルや爆弾を想像したかもしれない。しかし、歴史上、ミサイルや爆弾が、地表面上に「均等」に、「降った」ことは、ただの一度もないのである。それらは、圧倒的に、偏って、ある特定の地域ばかりに、「降った」。自然災害もまた然り。高温の回転物体たる地球が冷却する過程で、重金属などの分布には「偏り」が生ずる。その後地表面上に生物が繁殖するに当たっても、それらの「偏り」は変奏され、または強調される。古生物の遺骸からなる化石燃料の分布も、当然に「偏り」を含む。
私たち、は、そのような「不均等」な履歴を所与のものとして「文明」を作った。それぞれの土地に、そうでしかありえない、「歴史」が割り当てられた。こういうのをジオ・ボリティックス、地政学、と呼ぶ。
ユーラシア大陸西北端部という辺境に、たまたま生じた「ヨーロッパ文明」が、自分たちを「人間」と呼び、それが普遍的なものとナルシスティックに思い込んだ単なる笑い話が、本当に（笑）普遍化してしまったのは、彼らが「資本主義」を手にしたからに過ぎない（笑）。
「世界」は、圧倒的な「不均等」を所与の履歴として継承している。「資本主義」は、「差異」を検出して、それをまた別の新たな「差異」で置き換えることの・み・で、存続する。普遍的な「人類」や「人間性」、理想的に行動する「ホモ・エコノミクス」、十全な「自由意思」を備えた「市民」による社会契約、・・・、そんな絵空事がまことに絵空事でしかなかったのは、圧倒的な「不均等」に立脚しながら、そうであるが故に、その「不均等」をかけらも組み込むことができなかった思想だからだ（笑）。さらにいえば、そんな局所的な思想さえも、換骨奪胎され、ハイチの革命軍が「ラ・マルセレイズ」を以てナポレオン軍に対抗したように、言葉そのものの制御できない力により、伝播する。
おや?、どうしたんだい、なんか、「荒れて」いるね?、いや、いろいろ、あってね（笑）。ともあれ（笑）、ここでは「中性的」に、いや、この「リーマン球面」は、決して現実の地球などではない、ひとつの仮想的なものなのだと、無理にでも思い込もう。
k=n/aとして、単位面積あたりに「降る」個数として、これを一定と定めたとき、具体的な面積bは既にして「置き去り」にされているのだね?、aが無限化されても、それにともなって無限化されるのは、nであって、bという具体的な面積は、そこでは何の機能も持たない（笑）。無限大、に比べれば、有限な、ある特定の、値は、単なる0に過ぎない、というこのなのかな?
物理学的な「次元」で言えば、kは、個数/面積、ならばm=bkは、面積×(個数/面積)=個数、なるほど、「個数」というのは、「人」でも「匹」でも「個」でも「回」でも、「枚」でも「杯」でも（笑）、自然数（順序数）との一対一対応に還元できるから、「無次元」、単位系に依存しない、ある種「絶対的」な数、なのである。それで、とりあえず納得することにしよう。
では、ポアッソン分布とは、無限の広がりをもった球面上に、均一な割合で「何か」が降っている、ことのき、ほかならぬこの場所（面積は知らない）に、その「何か」が落ちてくる割合、を尋ねている、ことになる。
「世界」はこんなに広いのに、どうして、「私」だけに、「不幸」が降りかかる?、という嘆きに、この分布は答えてくれるかもしれない。生命保険会社が、保険料算出に際してこの分布を採用している、という話を聞いたことがある。特にそうでなければならない根拠があるわけではないが、ポアッソン分布には「不幸」の影が取り付いている。統計学の教科書でも入門書でも、まことに判で押した様に、挙げるのが、次の例、プロシア（プロイセン）の10個の騎兵大隊において、20年間にわたる調査、したがって、延べ10×20=200「大隊×年」において、軍馬に蹴られて死亡した兵士の数を、大隊ごとに割り振った統計、
| 死亡数 | 0 | 1 | 2 | 3 | 4 |
| 大隊数 | 109 | 65 | 22 | 3 | 1 |
19世紀の後半に存在したある国家のエピソードであるが、数理統計学の単位をごまかしのレポートで掠め取った昔から（笑）、この例示には何か愉快でない記憶が纏わりついていたのは、もちろん、見知らぬ人の「死」を、かなり不躾な手つきで、操作しているからだね。
もう少しニュートラルな「読み替え」を施してみたい。「大隊」を広辞苑で引いてみたが、一人の司令官が具体的な戦闘行為を指揮できる最大規模、ということであるが、人数については語ってくれなかった。それを知らなければ、明日を知り得ない個々の兵士が、ほかならぬ「私」が今日軍馬に蹴られて死ぬかもしれない、と予想する「確率」がいかほどのものか？、想像できないのである。W某ペディア、はこういう時便利であって、詳細な論述が見つかった。旧・大日本帝国陸軍においては、凡そ、一大隊600名、とある。森鴎外らが留学してその兵制を学んだのがほかならぬプロシア（プロイセン）であるから、かの国においても同様、と判断してもそう悪くないだろう、これを採用する。話をすりかえてみる。
従業員600名程度の会社が10社ある。それら10社を20年間追跡してみて、懲戒免職された従業員が4人の会社が1社あった、3人の会社は3社あった、この3社が同一の会社であるか、また4人の懲戒免職者を出した会社と同一のものを含んでいるかは不明である、・・・、等々。大事なポイントは、懲戒免職、であって、例えば、減給処分、とかではないことである。「死」と等価であるには、ただ一度しか起りえないことでなければならない。
あるいは、3年生の生徒数が約600人である高校10校で、過去20年に、名門○○大学に合格した人数、などというのも悪くないだろう?、「不幸」でないたとえだし、やはり通常、一度しか起らないことだし。
一年間一大隊あたりの死者をmとして採用する、と、どの教科書にも書いてある。そうしてみる。
0×109+1×65+2×22+3×3+4×1=0.61
「あなた」が「今年」、懲戒解雇されるかもしれない、と予想するとき、それは、600人のうち、0.61人にしか起らない事なのだ、と安心でき、
「あなた」が「今年」、名門大学に合格できるかもしれない、と予想するとき、それは、600人のうち、0.61人にしか起らない事なのだ、と落胆するのである（笑）。
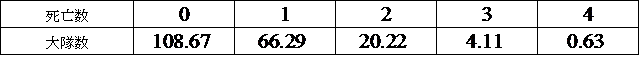
このmに対して、
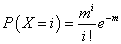
で計算すると、上の表の如きになり、確かに、「気持ち悪いほど」、「現実」に符合しているのである。「あなた」の不幸は、いや幸・不幸ともども（笑）単なる、mなる数値によって、どうやら、算出可能なようなのである（笑）。
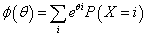
とおくと、0に関する第0積率φ(0)が、すべての場合の確率の和1を、0に関する第1積率φ(1)(0)が、期待値（平均）を、0に関する第2積率φ(2)(0)が、2乗の期待値を、あらわす道理であった。
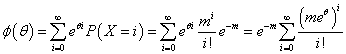
ここで、この式のシグマ記号の部分が、emeθであるから、と、数理統計学の教科書には、こともなげに書かれているのであるが（笑）、・・・、こんなことはプロフェッショナルには常識なのであろう?、最後まで（笑）プロフェッショナルではなかったのだから、今更嘆いても仕方がない（笑）。気がつくのに小一時間かかっただろうか?
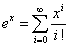
これは「マクローリン級数展開」を、指数関数g(x)=exに適用しているのである。では、「マクローリン級数展開」とはなんであったか?
xのn次多項式f(x)の各係数anは、以下のように、f(x)を順次微分して、0を代入することによって、得ることができる。
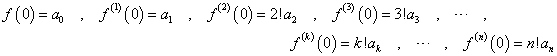
すなわち、
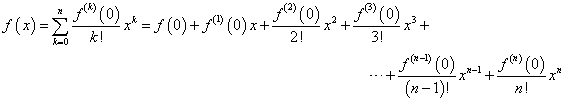
ならば、無限回微分可能な関数g(x)に対しては、これを用いて、xのn次多項式による近似が可能であることがわかる。第n次で止めてしまうと、そこに誤差が生じこれを「剰余項」と呼ぶのだが、そこの詳しい話には立ち入・れ・な・い・、ので、nをどんどん大きくすれば、どんどん真の値に近づくでしょ?、という雑な話で流しておく。
g(x)=exは何回微分しても、g(n)(x)=exだから、結局nに関わらず、つねに、g(n)(0)=1、したがって、
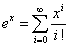
となる訳であった。積率母関数に話を戻すと、x=meθと思えばいいから、
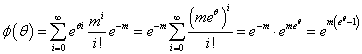
0に関する第0,1,2積率を求めてみると、
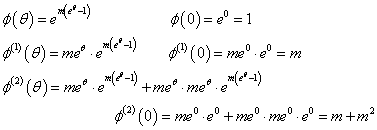
確かにすべての場合の確率の和は、1となっており、期待値は、E(X)=m、
分散は、V(x)=E(X2)-{E(X)}2=(m+m2)-m2=m
が得られたわけである。
- 一つは、二項分布B(n,p)の平均値np=mを一定として固定した上で、全試行回数nを限りなく大きくする。必然的に、一試行における確率pは、限りなく小さくなる、
- もう一つは、長さaの線分上にnこの何かが降ってくるとき、ある長さbに降ってくる確率は二項分布B(n,b/a)になるが、単位長さあたりに降る個数k=n/aを固定した上で、aを限りなく大きくすると、nもまた限りなく大きくなるであろう、
という二つの異なるアプローチがあったが、いずれの場合も、
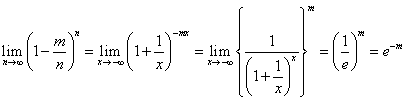
という極限値を求めるにあたって、自然対数の底、「ネイピア数」の定義を用いている。では、その証明に取り掛かろう（笑）。
段取りは次の如きである。
- まずは離散変数たる自然数に対応する「数列」の極限として、
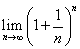
が収束すること。その収束値を仮にeと名付けるならば、その数は2と3の間の数であること、を示す。
その際、定理：「上に有界な単調増加数列は収束する」は自明なこととして（笑）使用する。「ε-δ論法」による証明は、何度読んでもあまり「ピンと来ない」（笑）が、一応ここに掲げておく。 - 次にこれを、連続変数たる全実数に拡げ、「関数」の極限として、
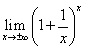
も、やはり同じ値に収束することを示す。とくに、x→-∞の場合が、ここでは必要なのだ。 - そして、今度は、すでに触れた指数関数の「マクローリン級数展開」を用いて、ネイピア数の近似値を求めてみる。
では、数列
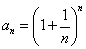が、2と3の間のある数に収束することを証明する。
- anが、単調増加であることを示す。
an≦an+1を示したい。
二項定理により、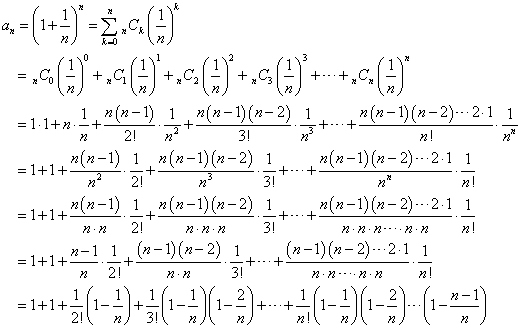
同様に、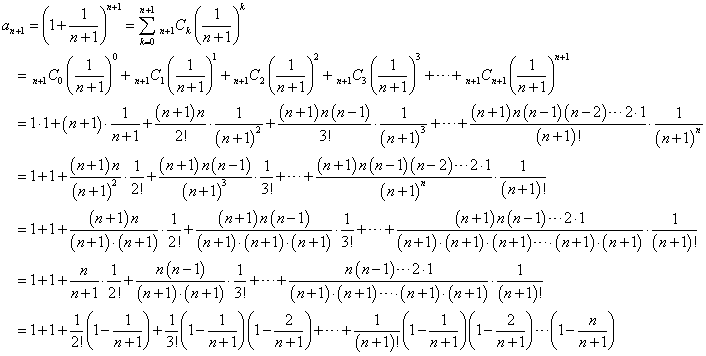
引き算すると、下のように、各項すべて正となるから、、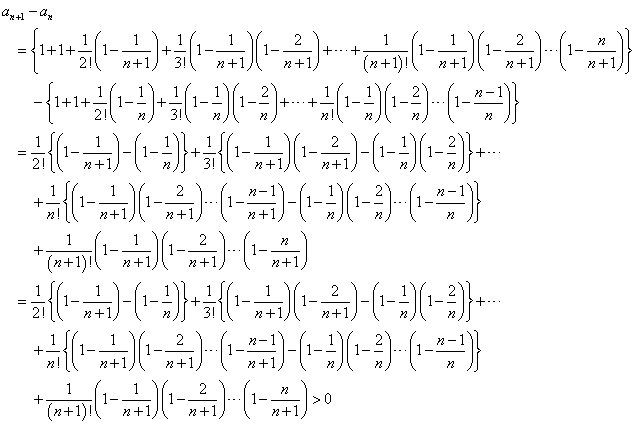
- anが、上に有界であることを示す。
- まず、k=0,1,2,・・・,nに対して、
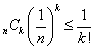であることを示す。
k=0のとき、nC0×1=1/0!
k=1のとき、nC1×(1/n)=1/1!
k=2,3,4,・・・,nに対して、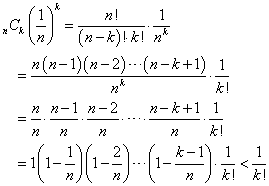
- 次に、n=1,2,3,・・・に対して、
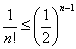であることを示す。数学的帰納法による。
- n=1のとき、1/1!=(1/2)0
- n=kに対して、
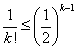と仮定する。
仮定より、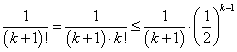
また、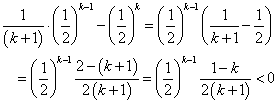
よって、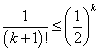
となり、n=k+1に対しても成立する。
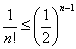が、示された。
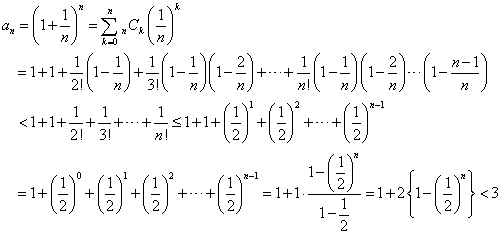
n=1,2,3,・・・に対して、an＜3、すなわち、anは上に有界であることが示された。 - まず、k=0,1,2,・・・,nに対して、
明らかに、an＞2であるから、
2＜e＜3である。
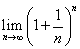が、2＜e＜3をみたす、eなる数に収束することが証明されたことを前提として、今度は、離散変数である自然数nから、連続変数である実数xに拡張し、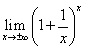もまた、同じeなる数に収束することを示したい。
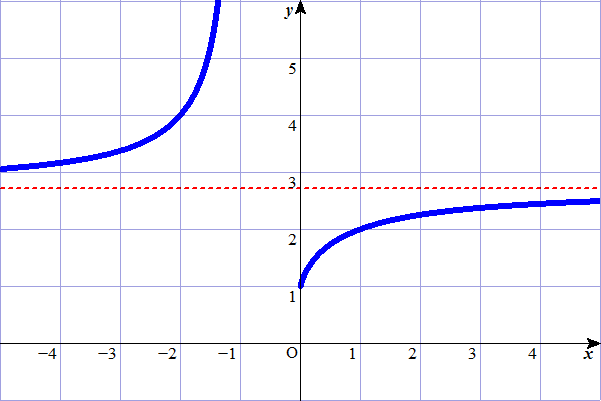
これは、
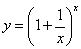のグラフであるが、ここでの目的としては、x→+∞のみならず、x→-∞に対しても同じくeに収束することを示したい。ところで、grapesというアプリケーションで、こともなげにこんなグラフを描いてくれるのだが、もちろんこの関数はx=0で定義されない。0の左方極限が+∞、右方極限が1、らしいのだが、それはまた別途証明が必要になる。
稠密な「実数」は、いかなる場合でも、ある自然数と、それと隣接する自然数の「間」にある。任意のxに対して、以下の不等式を満たす自然数nが必ずただひとつ、存在する。
n≦x＜n+1
x→+∞となるとき、nもまた、n→∞となるであろう。
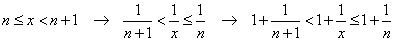
0＜n≦x＜n+1に対して、
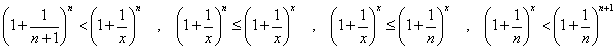
がそれぞれ成り立つから、結局、
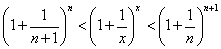
ここで、すでに得られた「ネイピア数」eの定義より、
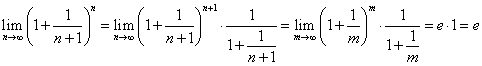・・・(1)
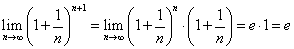・・・(2)
である。(1)では、m=n+1とすると、n→∞ならば、m→∞、を用いている。
こうして「はさみうちの原理」より、
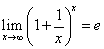
が得られたわけである。次に、
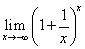
もまたeに収束する、と言いたいのだが、そのためには、どのような技巧が必要であろうか？
y=-xとおくと、x→-∞に対して、y→∞
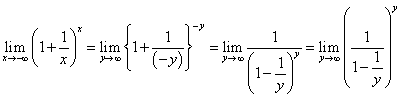
さらに、
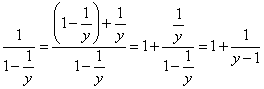
であるから、さらにz=y-1とおくと、y→∞に対して、z→∞であるから、
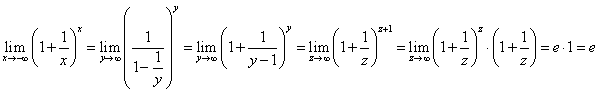
が、得られたわけである。
二項分布を極限化するにあたって、「スターリングの公式」なるものが必要となる。これは、n!の近似式で、
「エクセル」で計算できるのはこの辺が限界なのであるが、なるほどすぐれた近似である。
この近似式を導くのが、もう、あらかた忘れたが(笑)大変な、難行で、・・・、その前提として、次の二つの事柄を用意しておかなければならない。
- 「ワリスの等式」
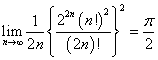
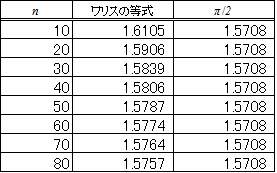
これも、ここまでしか計算できないが、急速に収束していく有様は、窺える。 - もう一つは、
というもので、これは、マクローリン級数展開を、関数1/(1-x)に適用した次の結果、から導かれる段取りである。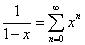
0≦x≦π/2に対して、0≦sinx≦1であるから、
n=2,3,4,・・・に対して、
(sinx)2n+1≦(sinx)2n≦(sinx)2n-1 ただし、等号成立は、x=0,π/2
絶対値が１より小さいものは、他数回繰り返し掛けると、その絶対値はますます小さくなる、その理屈から出発する。このような大小関係を有した関数を、同じ積分区間0≦x≦π/2で積分すると、
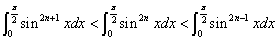
ここで等号がなくなってしまったのは、3つの関数が等しかったのは、ただx=0,π/2の2点だけで、それ以外の点で、恒等的に等しい、訳では決してないからだ。ここで、
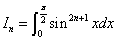とおくと、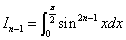
また、
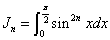とおくと、上の不等式は、
In＜Jn＜In-1
これを、「はさみうちの原理」に利用する予定である。n=1,2,3,・・・に対して、部分積分法で計算すると、
ここで、
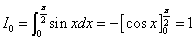であるから、
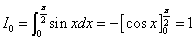
したがって、
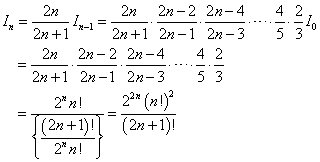
同様にして、
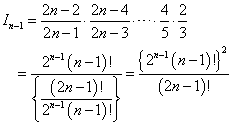
同様にn=2,3,4,・・・に対して、
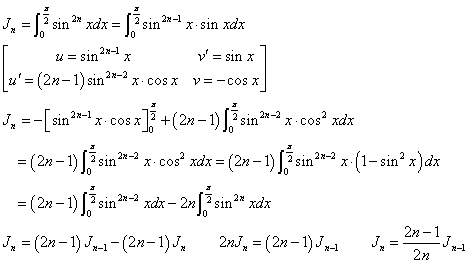
ここで、
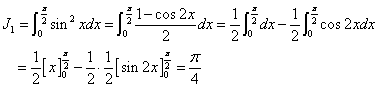
であるから、
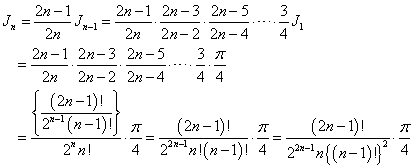
よって、
In＜Jn＜In-1
より、
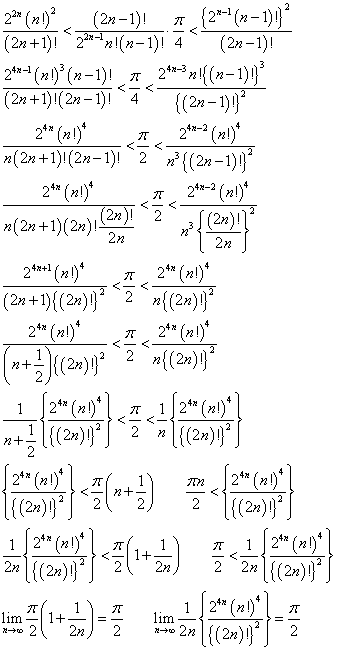
なるほど、これが「ワリスの等式」、である。2が一つ足りない、、nが多過ぎる、と一喜一憂して、ここに至るまで3時間ばかりかかっている。猫たちに振舞うための「沖縄近海産かつお」が茹で上がるのに、十分な時間であった(笑)。
まず、
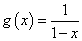について、マクローリン級数展開を行う。順次微分すると、
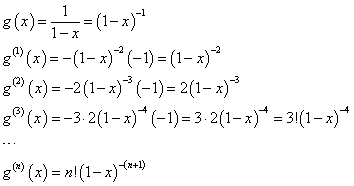
であるから、
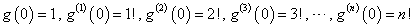
ここで、一般に、
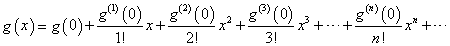
であるから、
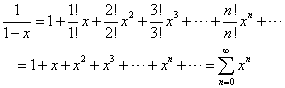
この式は、xに関する「恒等式」であるから、xの代わりに、どのような文字を代入しても、成立する。そこで、-xを代入するわけだ。
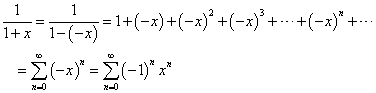
さてここで、唐突ではあるが(笑)、
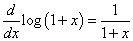
であることに思い至るのである。logは自然対数、つまり底は、ネイピア数である。自然対数をば、lnと表記するのが、工学系では常識だったと、ろくに学校行ってないくせに(笑)、思い込んでいたが、そうでもない「業界」もありそうなので、logにしておく。逆に、定積分の形で書き表すと、
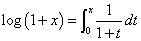
ここに、上のマクローリン級数展開の結果を適用すると、
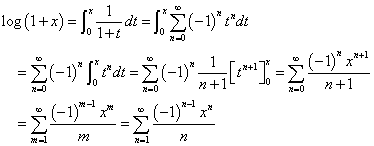
一行目から二行目の変形には、項別積分が可能であることを当然の前提にしている。本当はそれについても検討が必要なのかもしれないが、わからないので(笑)省略。二行目から三行目への変形ではm=n+1すなわち、n→∞なら、m→∞を用い、しかる後、再びnに戻した。
ここでもまた、これはxの「恒等式」であろう、という理屈で、xに-xを代入し、
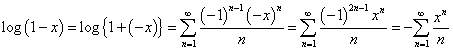
では、これらの材料を用いて、
なるほど偶数番目の項は消えて、奇数番目の項は2倍になり、こうして、予定通り(笑)の結果となった。
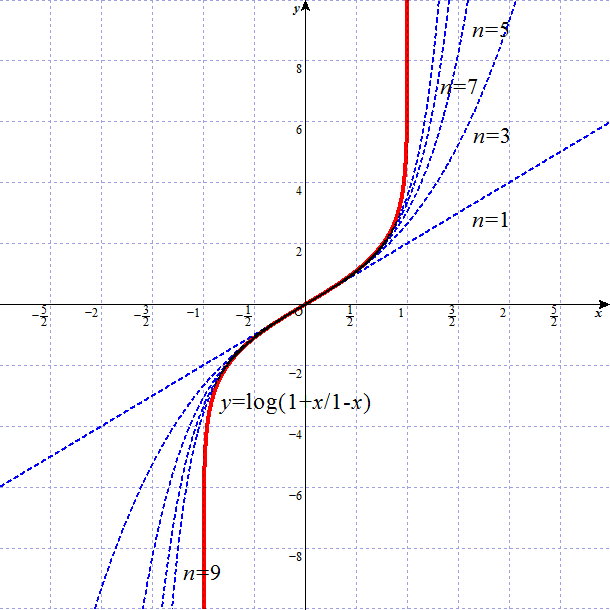
グラフを描いてみた。なるほど項の数を増やすほど、近似はよくなる、という、当然の(笑)、結果となった。
これを証明する道具として、
- ワリスの等式
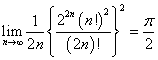
- 次のような対数関数の級数展開
・・・(1)
を示したいのだから、
を導きたいのである。この数列は収束する、その収束値は、ほかならぬ1である、と言いたい。いわゆる「はさみうちの原理」、より正確に言うと、
- 上に有界な単調増加数列は収束する、
- 下に有界な単調減少数列は収束する、
n!がこのような式で「近似」、「〜」は近似の記号である、出来るというのなら、ずばり、次のような式がn!そのものであってよかろう？、と言うのである。
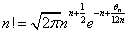ただし、0＜θn＜1・・・(2)
数学の教科書というものは、概して「不親切」なもので、「こうすれば、うまくいく。うまくいったのだから、いいではないか？」とばかりに、どうして「こうする」ことを「思いつく」に至ったか、のプロセスは、伏せられているのである。それ自体は、全然悪いことではない。小説でも映画でも、「舞台裏」が全て明らかにされたら、却って退屈であろう？、「不親切」な記述から、その「舞台裏」を読み解くことこそが、数学の教科書、などという、決して心躍る筈もない書物を読む、「楽しみ」の一つなのである。
でも、今回は、全然「楽しめ」なかった。へとへとになりながらも、やっとなんとか、すべての数式をたどり終えて、「納得」出来た後でさえ、結局、どうしてθn/12nが、唐突に「思いつか」れたのか、全然想像もつかない。
しかし、考えてみれば、それは、話が「逆」なのである。この式を発見した、スターリング氏については、どなたなのか存じ上げないが、その人が、唐突に、n!はこれに似ている、とばかりに(1)式を「思いついた」わけはないので、そうではなく、推論の過程で、(2)式の方が、先に転がり出てきたはずなのである。その過程を知りえない、「我々」凡人としては、どこから「１２」が飛び出してくるのか、さっぱり見当もつかないが、さしあたり、受け入れるしかないのである。
以前も掲げたこの数表を見る限り、スターリングの公式なる近似は、真の値より、少し「少なめに見積もる」ものであるらしい。ならば、確かに、(1)から(2)への変形において、eθn/12n＞1が乗ぜられているのは、頷けるのである。
ここで、θnなるもの、その添字が示すように、nの「関数」なのである。しかしその形は、きっと最後まで、わからない、ただ、いかなるnに対しても、0と1との間のある数を取る、ことが分かればよいのであろう。
0＜θn＜1であるから、
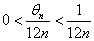従って
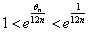さらに、
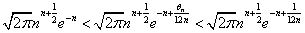
であるから、
、
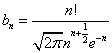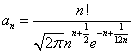とおけば、任意のnに対して、bn＞anと言える。
証明したいのは、bnの極限が、1だ、ということなのだから、これで「はさみうち」の、片側は抑えられたことになるのだろう。私、「有界」って言葉の定義、いまいちピンと来てないんだけど、bnには、それより小さいものがいつも、ある、anには、それより大きいものがいつも、ある、というのだから、これで、
- bnは下に「有界」であり、
- anは上に「有界」である、
- bnが、単調減少であること、
- anが、単調増加であること、
なのだから、きっと同じ値であり、うまくいけば、それがほかならぬ1である、と言えればよいのである。
今日のところは、ここまでにする。
anが、単調増加であること、の方から始める。
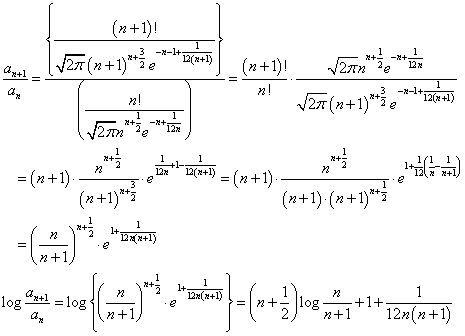
ここで、既に準備した
を用いることになる。
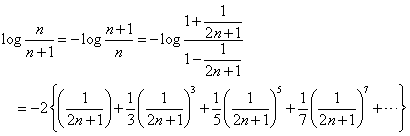
ここでは、
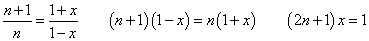、という変形を使っている。
さて、これを元の式に戻すと、
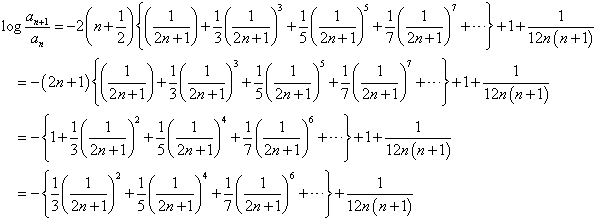
だんだん、何がしたかったのかわからなくなってくるが、anが、単調増加であること、を示したいのであるから、右辺が、正であることを言えばよいのである。そこで、
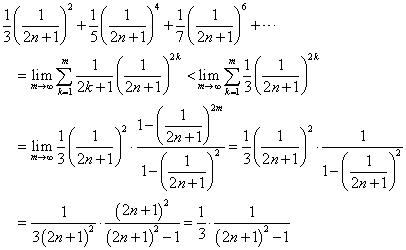
これは、上式の中かっこの中の各項が、調和数列（自然数からなる等差数列の逆数の数列）と、等比数列の積になっているから、調和数列部分を初項の1/3に固定した等比数列より、小さかろう？、という論理である。これを再び元式に戻すと、
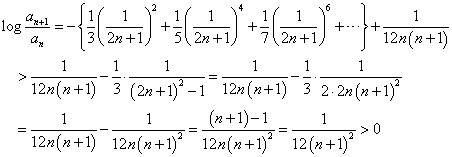
なるほど、示された。an+1/an＞1すなわち、an+1＞an、数列anは、単調増加である。
bnが、単調減少であること、も、ほぼ、同じロジックで証明できる。
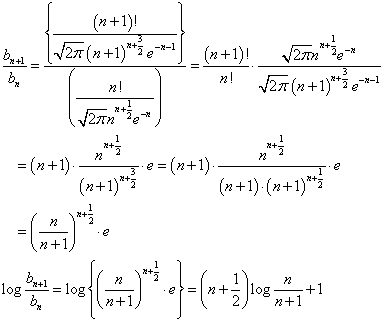
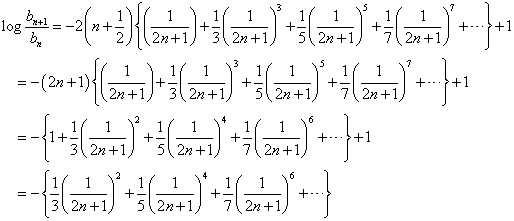
今度は、中かっこ内のすべての項は、ことごとく正である。だから、log(bn+1/bn)＜0、すなわち、bn+1/bn＜1、すなわち、bn+1＜bn、bnは単調減少である。
こうして、
- bnは下に「有界」で、単調減少であること、
- anは上に「有界」で、単調増加であること、
が示されたのである。つまり、どちらも、収束する。しかも、
であるから、その収束値は、同一でなければならない。これをαと名付ければ、
a1＜a2＜a3＜・・・＜an-1＜an＜・・・＜α＜・・・＜bn＜bn-1＜・・・＜b3＜b2＜b1
となるであろう。ここで初めて、
をみたす、0＜θn＜1が見つかるはずだ、と言えるのである。そのαが、ほかならぬ1だと言いたいのだが、今回は、ここまで。
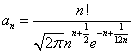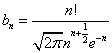、 で、なおかつ、an＜α＜bnだからこそ、
ただし、0＜θn＜1
と置くことを「思いつけた」のだな！、そして、分母に「12」なる数字が用いられているのも、log(an+1/an)＞0を導く最終段階で、他の項の分母の係数が12になっているから、というだ・け・の理由なんだな！、こうして、やっと「舞台裏」が、読み解けた、というところで納得しよう。
では、そのαが、ほかならぬ「1」であることを示す。ここにやっと「ワリスの等式」が登場するようである。
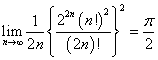
ほとんど「無理矢理」、αの式を材料にして、この式に「似せていく」のである。さしあたり、「ワリスの等式」の左辺に現れているもので、「似ている」といえば、n!と(2n)!くらいのものであるから、まず、これらをαを用いて表す。
- は、任意の自然数nに対して、0＜θn＜1が存在する、と言っている。
- ならば、この式のnをそっくり2nに入れ替えて、自然数2nに対しても、
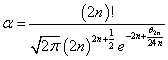をみたす、0＜θ2n＜1が存在する、と言ってもよかろう？
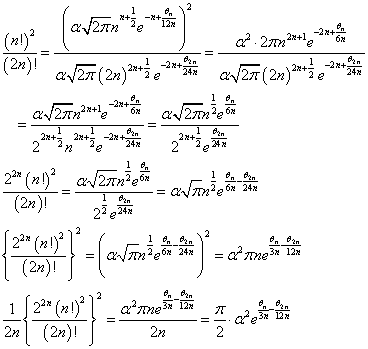
なんだか、右辺にπ/2が出てきて、「気持ち悪い」くらい「似て」きたではないか？
ここで、
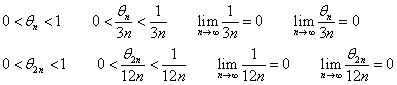
であるから、
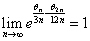
これを用いて両辺の極限をとると、
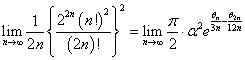
左辺は「ワリスの等式」より、π/2、右辺は、(π/2)・α2、
つまり、α2=1、
an＜α＜bnで、an＞0だから、α=1
出来ました。何が出来たのか？、というと、十分大きいnに対しては、「スターリングの公式」
を用いてよいことが、示されたのである。